T
Teach Me AnythingTMA
Video History
Page 20 / 44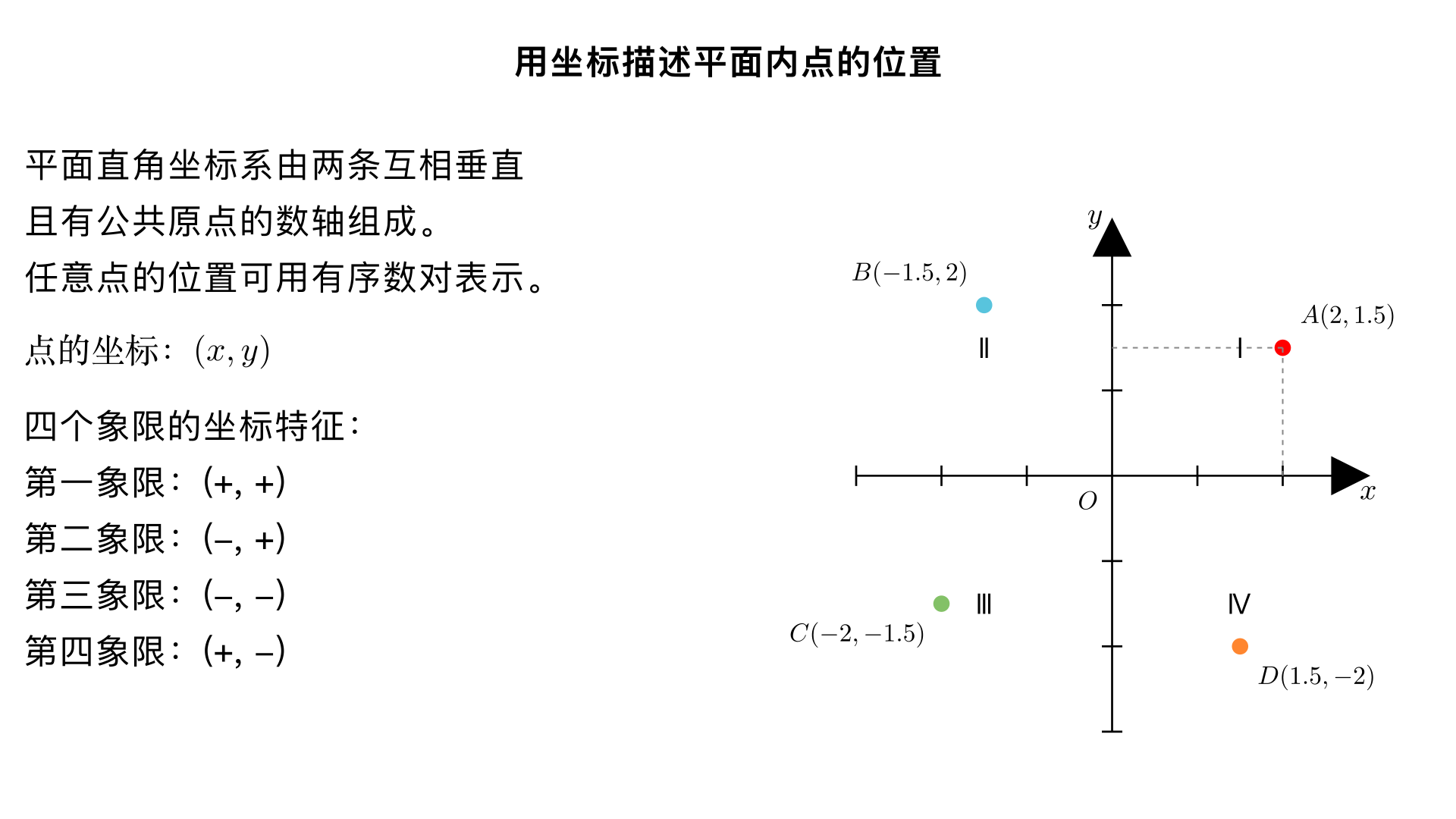
▶
七年级数学 / 平面直角坐标系 / 用坐标描述平面内点的位置 本小节的核心是掌握平面直角坐标系的构成,并能通过有序数对精准描述平面内任意点的位置,同时理解不同区域内点的坐标特征。 一、平面直角坐标系的基本构成 平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的,具体要素如下: 数轴 横轴:水平方向的数轴,称为 x 轴(或横轴),通常规定向右为正方向。 纵轴:竖直方向的数轴,称为 y 轴(或纵轴),通常规定向上为正方向。 原点:x 轴与 y 轴的公共交点,记作 O,其坐标为 (0,0) 。 象限:x 轴和 y 轴将平面分成四个区域,按逆时针方向依次为第一象限、第二象限、第三象限、第四象限(坐标轴上的点不属于任何象限)。 二、用坐标描述点的位置的方法 平面内任意一点的位置都可以用有序数对 (x,y) 来表示,这个有序数对称为该点的坐标,具体确定步骤如下: 过该点作x 轴的垂线,垂足在 x 轴上对应的数即为该点的横坐标(记为 x); 过该点作y 轴的垂线,垂足在 y 轴上对应的数即为该点的纵坐标(记为 y); 按 “横坐标在前,纵坐标在后” 的顺序写成有序数对 (x,y) ,即可描述该点的位置。 例:若点 A 到 x 轴的垂线对应 x 轴上的数 3,到 y 轴的垂线对应 y 轴上的数 2,则点 A 的坐标为 (3,2) 。 三、不同区域内点的坐标特征 根据坐标的符号,可快速判断点所在的区域,具体特征如下: 点的位置 横坐标 (x) 符号 纵坐标 (y) 符号 示例 第一象限 正 正 (2,3) 第二象限 负 正 (−2,3) 第三象限 负 负 (−2,−3) 第四象限 正 负 (2,−3) x 轴上 任意实数 0 (5,0) 、 (−3,0) y 轴上 0 任意实数 (0,5) 、 (0,−3) 原点 0 0 (0,0) 四、易错点提醒 坐标是有序数对,横坐标和纵坐标的顺序不能颠倒,例如 (3,2) 和 (2,3) 表示平面内两个不同的点; 坐标轴上的点不属于任何象限,需注意区分 “象限内的点” 和 “坐标轴上的点” 的坐标差异。
▶
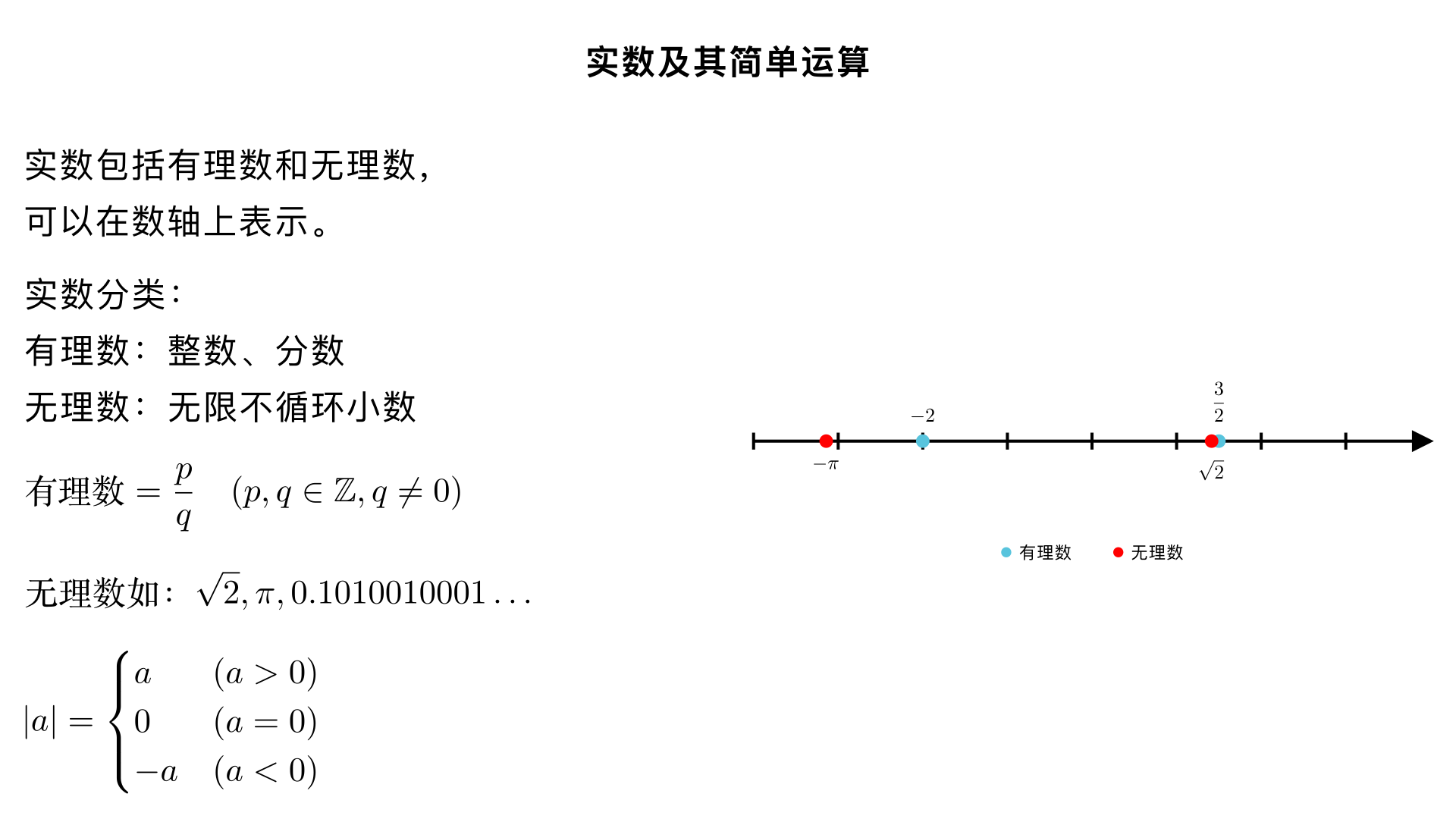
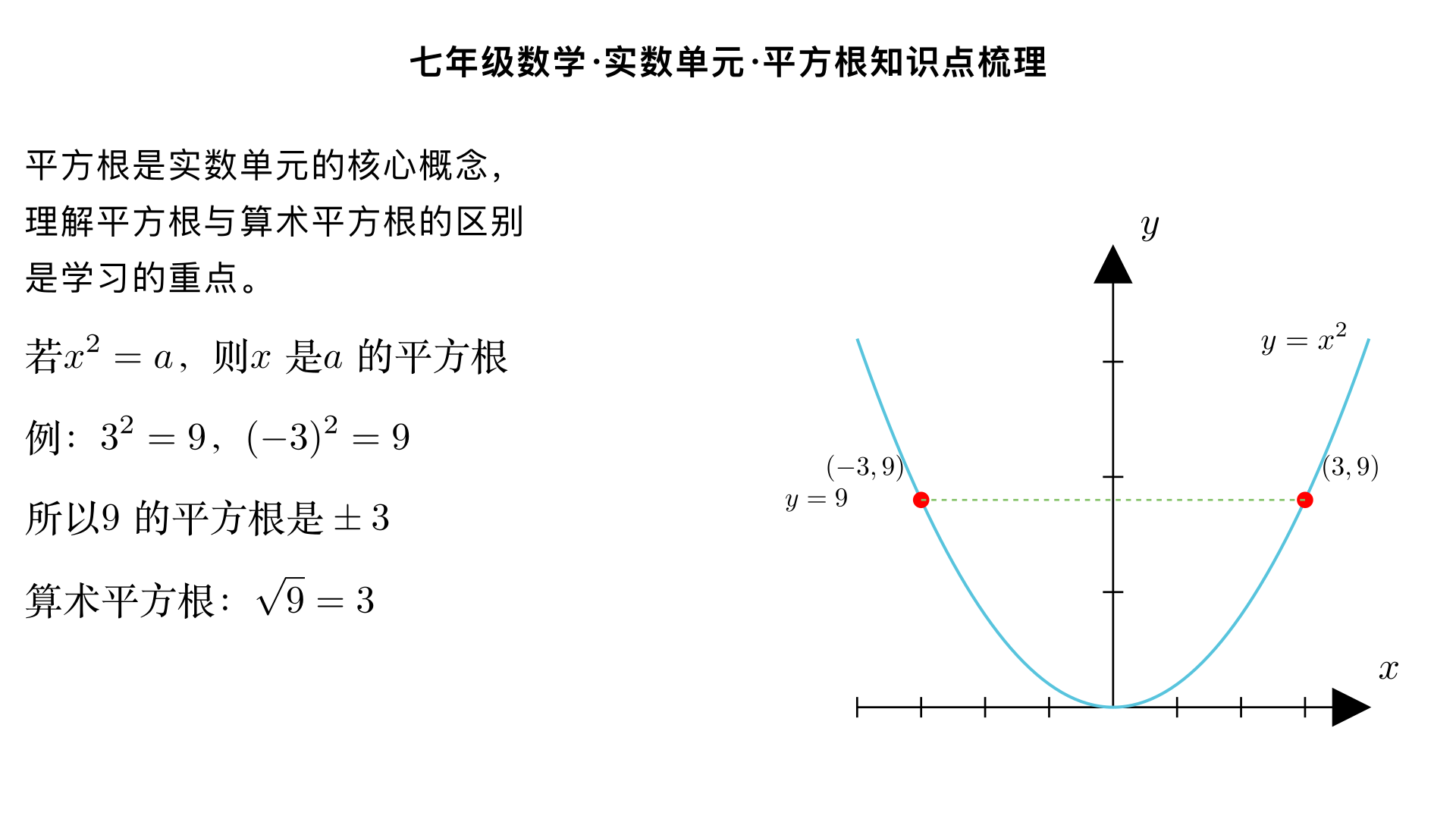
七年级数学 / 实数 / 实数及其简单运算 一、实数的概念与分类 1. 实数的定义 有理数和无理数统称为实数,也就是说,所有可以在数轴上表示出来的数都属于实数。 2. 实数的分类 (1)按定义分类 实 数 有 理 数 整 数 正 整 数 负 整 数 分 数 正 分 数 负 分 数 无 理 数 : 无 限 不 循 环 小 数 有理数的本质:可以表示为两个整数之比( q p ,其中 p,q 为整数且 q =0 ),其小数形式为有限小数或无限循环小数。 无理数的常见类型: 开方开不尽的数,如 2 、 3 、 5 等; 特定的无限不循环小数,如圆周率 π ( π≈3.1415926… ); 有规律但不循环的无限小数,如 0.1010010001… (相邻两个 1 之间 0 的个数依次加 1)。 (2)按正负性分类 实 数 正 实 数 正 有 理 数 正 无 理 数 负 实 数 负 有 理 数 负 无 理 数 二、实数的相关性质 实数与数轴的关系:每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都对应一个实数,即实数与数轴上的点一一对应。 相反数:实数 a 的相反数是 −a ,0 的相反数是 0。互为相反数的两个实数在数轴上对应的点关于原点对称,且它们的和为 0(即 a+(−a)=0 )。 绝对值:实数 a 的绝对值 ∣a∣ 的几何意义是数轴上表示 a 的点到原点的距离,代数意义为: ∣a∣= ⎩ ⎨ ⎧ a 0 −a (a>0) (a=0) (a<0) 倒数:非零实数 a 的倒数是 a 1 ,0 没有倒数。互为倒数的两个实数的积为 1(即 a⋅ a 1 =1 )。 三、实数的简单运算 1. 运算法则 实数的运算律和运算法则与有理数一致,核心运算包括加、减、乘、除、乘方,以及开平方(算术平方根),具体如下: 加法:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两数相加得 0;一个数与 0 相加仍得这个数。 减法:减去一个数,等于加上这个数的相反数,即 a−b=a+(−b) 。 乘法:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘都得 0;多个非零实数相乘,积的符号由负因数的个数决定(负因数个数为偶数时积为正,奇数时积为负)。 除法:除以一个非零数,等于乘这个数的倒数,即 a÷b=a⋅ b 1 (b =0) ;两数相除,同号得正,异号得负,并把绝对值相除;0 除以任何非零数都得 0。 乘方:求 n 个相同因数 a 的积的运算叫乘方,记作 a n ,其中 a 是底数, n 是指数,结果叫幂。正数的任何次幂都是正数,负数的偶次幂是正数,负数的奇次幂是负数,0 的正整数次幂是 0。 开平方:若 x 2 =a(a≥0) ,则 x 叫做 a 的平方根,其中非负的平方根叫做 a 的算术平方根,记作 a ( a≥0 );0 的算术平方根是 0,负数没有平方根。 2. 运算顺序 先算乘方、开平方,再算乘除,最后算加减; 有括号的先算括号内的(先小括号,再中括号,最后大括号); 同级运算从左到右依次进行。 3. 典型例题 例 1:计算 4 +∣− 2 ∣−(−1) 解:原式 =2+ 2 +1=3+ 2 例 2:计算 (−2) 2 − 9 +π 0 ( π 0 =1 ,任何非零数的 0 次幂为 1)解:原式 =4−3+1=2 四、易错点提醒 混淆 “有理数” 和 “无理数” 的概念,误认为带根号的数都是无理数(如 4 =2 是有理数); 忽略绝对值运算的分类讨论,如计算 ∣a−1∣ 时未考虑 a 与 1 的大小关系; 进行开平方运算时,忘记算术平方根是非负数,如误将 4 算成 ±2。
▶
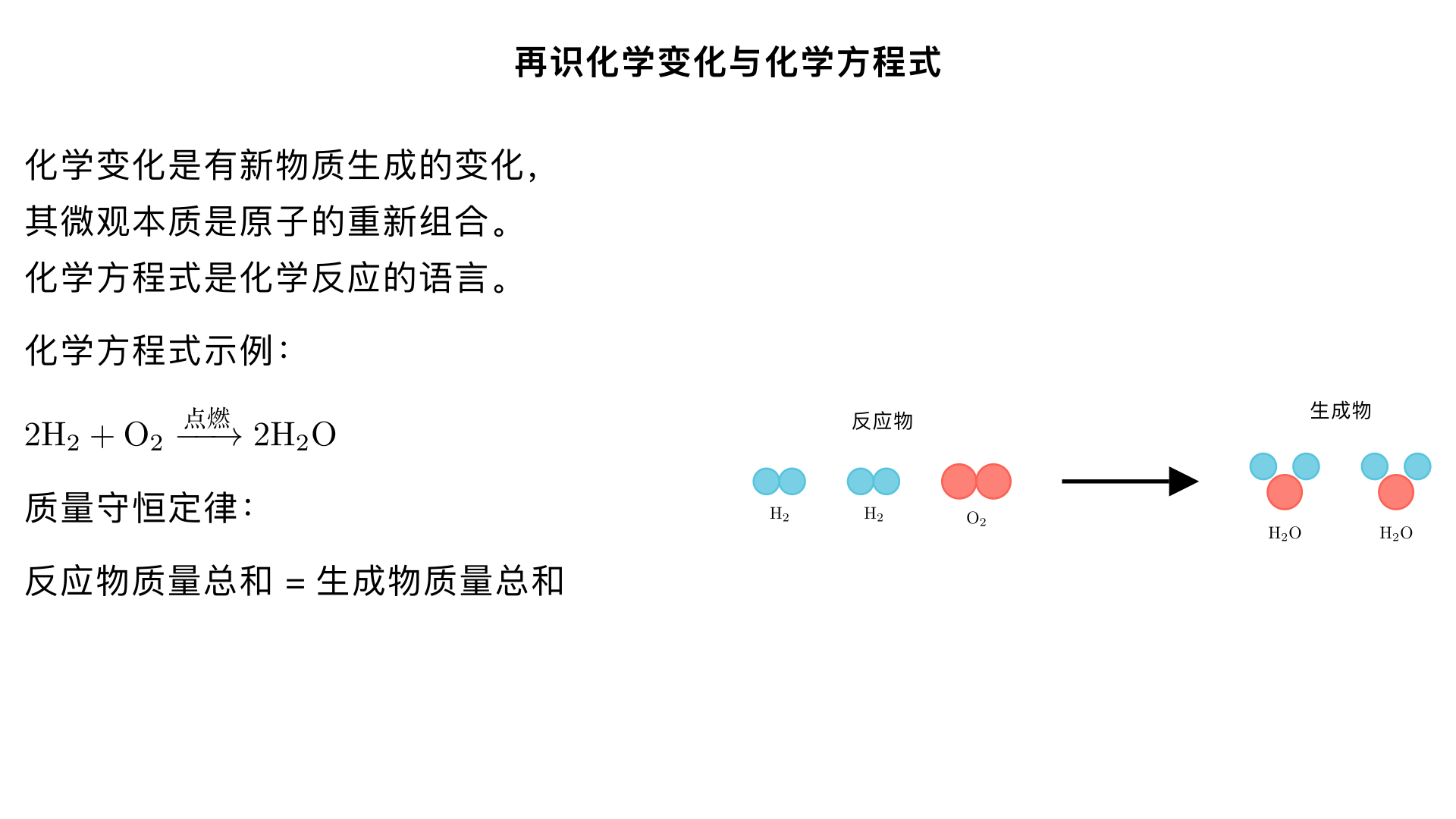
九年级化学:再识化学变化与化学方程式 一、化学变化的本质与特征 1. 化学变化的定义 化学变化(又称化学反应)是有新物质生成的变化。这是区别于物理变化的根本特征。 微观本质:反应物分子分解成原子或离子,原子重新组合形成新分子。 2. 化学变化的特征现象 生成新物质(最本质特征) 颜色改变(如铁生锈变红) 放出气体(如碳酸盐与酸反应产生 CO₂) 生成沉淀(如澄清石灰水遇 CO₂变浑浊) 能量变化(放热、吸热、发光) 3. 化学变化与物理变化对比 对比项 化学变化 物理变化 有无新物质生成 有 无 分子变化 分子破裂,原子重组 分子间隔改变,分子本身不变 举例 燃烧、生锈、食物变质 水结冰、酒精挥发、矿石粉碎 判断关键:看变化后是否生成了与原物质性质完全不同的新物质。 二、化学方程式:化学反应的语言 1. 化学方程式的概念 化学方程式是用化学式表示化学反应的式子。 示例:2H₂ + O₂ 点 燃 2H₂O(氢气和氧气在点燃条件下生成水) 2. 化学方程式的意义 (1) 质的方面:表明反应物、生成物和反应条件 (2) 量的方面: 粒子个数比:化学计量数之比(如 2:1:2,表示 2 个氢分子:1 个氧分子:2 个水分子) 质量比:(相对分子质量 × 化学计量数) 之比 2H₂ + O₂ 点 燃 2H₂O (2×2):(32):(2×18) = 4:32:36 = 1:8:9 3. 化学方程式的书写原则 (1) 以客观事实为基础:绝不能臆造不存在的物质或反应 (2) 遵守质量守恒定律:方程式两边各元素的原子种类和数目必须相等 三、化学方程式的书写步骤:"一写二配三注四查" 1. 一写:写出反应物和生成物的化学式 反应物写左边,生成物写右边,中间用短线 "—" 连接 多种物质间用 "+" 号连接 例:KMnO₄ — K₂MnO₄ + MnO₂ + O₂ 2. 二配:配平化学方程式(核心步骤) 通过调整化学式前的化学计量数,使两边原子种类和数目相等 只能改变系数,不能改动化学式右下角的数字 3. 三注:注明反应条件和生成物状态 反应条件:点燃、加热 (△)、催化剂 (MnO₂等)、通电等,写在等号上方 生成物状态: 气体:↑(反应物中无气体时) 沉淀:↓(反应物中无固体时) 例:2KMnO₄ Δ K₂MnO₄ + MnO₂ + O₂↑ 4. 四查:检查方程式是否正确 化学式是否正确 是否配平(原子守恒) 条件和状态标注是否恰当 化学计量数是否为最简整数比 四、化学方程式的配平方法 1. 最小公倍数法(最基本方法) 适用:某元素在方程式两边各出现一次且原子个数相差较大 步骤: 找出两边出现次数多且原子个数差异大的元素 求该元素原子个数的最小公倍数 用最小公倍数除以原子个数,得到相应物质的系数 再配平其他元素 示例:P + O₂ — P₂O₅ 氧原子:左边 2 个,右边 5 个,最小公倍数 10 O₂系数:10÷2=5;P₂O₅系数:10÷5=2 P 系数:4(使磷原子守恒) 结果:4P + 5O₂ 点 燃 2P₂O₅ 2. 奇数配偶法 适用:某元素在方程式两边出现次数多且一边为奇数,一边为偶数 步骤: 选择出现次数最多且一奇一偶的元素 将奇数原子的化学式前配上最小的偶数 (2) 再依次配平其他元素 示例:C₂H₂ + O₂ — H₂O + CO₂ 氧原子:H₂O 中为奇数,先在 H₂O 前配 2 C₂H₂系数:2(使氢原子守恒) CO₂系数:4(使碳原子守恒) O₂系数:5(使氧原子守恒) 结果:2C₂H₂ + 5O₂ 点 燃 2H₂O + 4CO₂ 3. 观察法 适用:较简单的反应或某物质化学式较复杂 步骤: 从化学式复杂的物质入手,确定其系数 推导其他物质的系数 示例:H₂O + Fe — Fe₃O₄ + H₂ Fe₃O₄中有 3 个铁原子和 4 个氧原子 H₂O 前配 4(提供 4 个氧原子) Fe 前配 3(提供 3 个铁原子) H₂前配 4(使氢原子守恒) 结果:4H₂O + 3Fe 高 温 Fe₃O₄ + 4H₂ 五、根据化学方程式的简单计算 1. 计算依据 质量守恒定律和化学方程式中各物质的质量比(定值) 2. 计算步骤(设、写、关、列、答) 示例:实验室加热分解 6.3g 高锰酸钾,理论上能制得氧气多少克? (1) 设:设未知量解:设可制得氧气质量为 x (2) 写:写出配平的化学方程式2KMnO₄ Δ K₂MnO₄ + MnO₂ + O₂↑ (3) 关:写出相关物质的质量关系2KMnO₄ Δ K₂MnO₄ + MnO₂ + O₂↑2×158 = 316 326.3g x (4) 列:列比例式求解 32 316 = x 6.3g x = 316 32×6.3g ≈ 0.64g (5) 答:简明写出答案答:理论上可制得氧气 0.64g。 3. 计算注意事项 设未知量时不带单位 化学方程式必须配平 代入计算的必须是纯净物的质量 单位要统一,计算结果带单位 六、常见化学反应类型(四大基本类型) 1. 化合反应:"多变一" 定义:由两种或两种以上物质生成一种物质的反应 通式:A + B + ... → C 示例: 2Mg + O₂ 点 燃 2MgO C + O₂ 点 燃 CO₂ 2. 分解反应:"一变多" 定义:由一种物质生成两种或两种以上物质的反应 通式:C → A + B + ... 示例: 2KClO₃ MnO 2 Δ 2KCl + 3O₂↑ H₂CO₃ → H₂O + CO₂↑ 3. 置换反应:"一换一" 定义:一种单质与一种化合物反应,生成另一种单质和另一种化合物 通式:A + BC → AC + B 示例: Fe + 2HCl → FeCl₂ + H₂↑ Zn + H₂SO₄ → ZnSO₄ + H₂↑ 4. 复分解反应:"双交换,价不变" 定义:两种化合物互相交换成分,生成另外两种化合物 通式:AB + CD → AD + CB 示例: HCl + NaOH → NaCl + H₂O(中和反应) AgNO₃ + NaCl → AgCl↓ + NaNO₃ 七、质量守恒定律:化学方程式的理论基础 1. 质量守恒定律内容 参加化学反应的各物质的质量总和等于反应后生成的各物质的质量总和。 2. 微观解释 化学反应前后: 六个不变:元素种类不变、元素质量不变、原子种类不变、原子数目不变、原子质量不变、物质总质量不变 两个一定变:物质种类一定变、分子种类一定变 可能变:分子总数可能变 3. 应用 (1) 推断物质的化学式例:CO₂ + 3H₂ 催 化 剂 X + H₂O,求 X 反应前:C (1)、O (2)、H (6) 反应后 H₂O 中有 O (1)、H (2),则 X 中应有 C (1)、O (1)、H (4) 所以 X 为 CH₃OH(甲醇) (2) 计算物质的质量例:12g A 与 18g B 恰好完全反应,生成 28g C,求生成 D 的质量 根据质量守恒:12g + 18g = 28g + m (D) m(D) = 2g 总结:化学变化与化学方程式的关系 化学方程式是化学变化的 "密码",它不仅能简洁地表示化学反应,还能定量揭示反应物与生成物之间的关系。掌握化学方程式的书写和计算,是理解化学变化本质的关键。 学习要点回顾: 化学变化的本质是有新物质生成,微观上是原子的重新组合 化学方程式遵循质量守恒定律,体现了化学反应的质和量两方面意义 化学方程式书写的核心是配平,使两边原子种类和数目相等 四大基本反应类型反映了化学反应的基本规律,帮助我们理解和记忆各类反应 课后练习建议: 熟练书写常见反应的化学方程式并配平(如氧气、二氧化碳的制取) 练习根据化学方程式进行简单计算,特别是纯净物与含杂质物质的换算 观察生活中的化学变化,尝试用化学方程式表示(如铁生锈、天然气燃烧)
▶
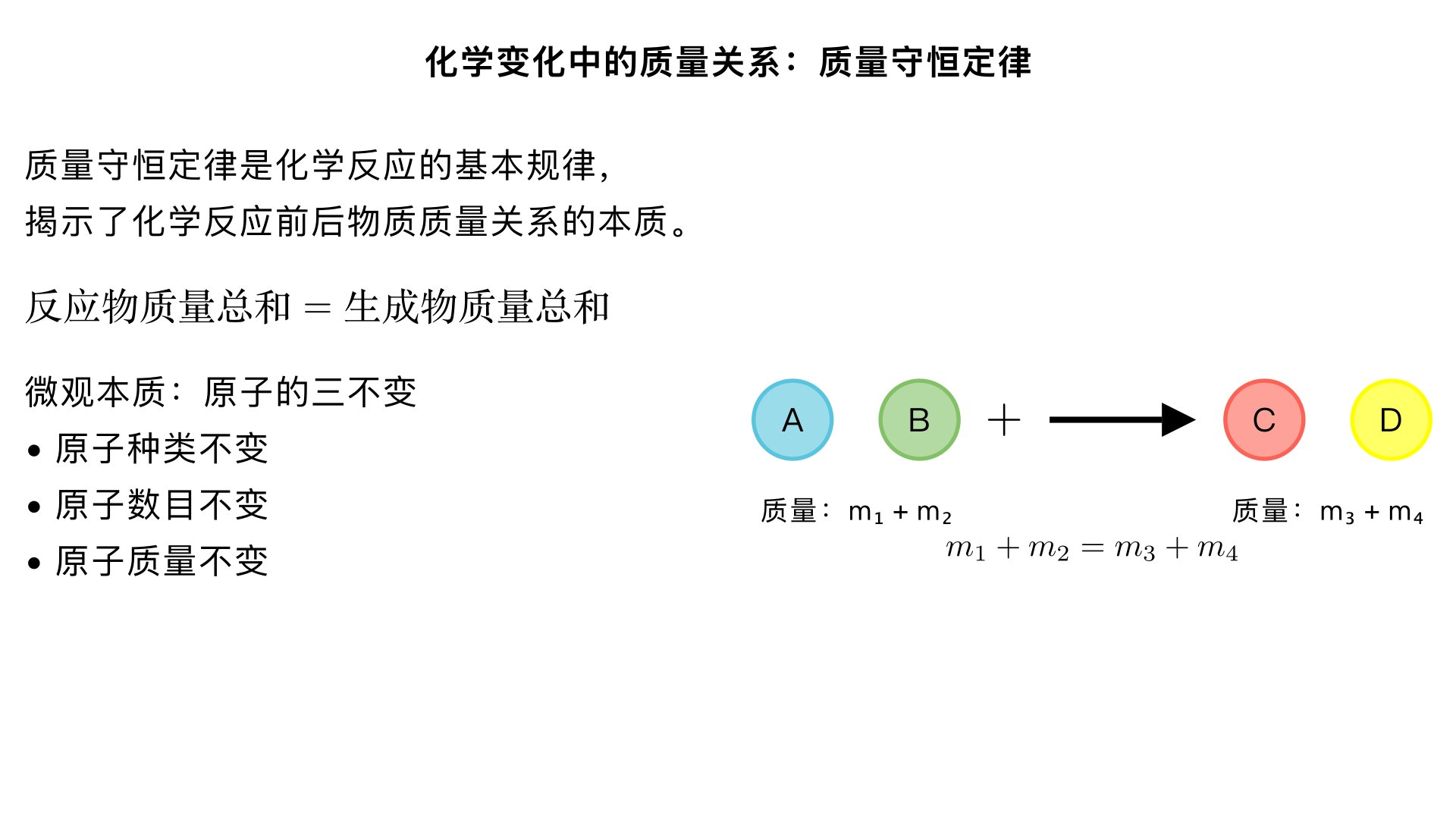
化学变化中的质量关系:质量守恒定律 一、质量守恒定律的内容 参加化学反应的各物质的质量总和等于反应后生成的各物质的质量总和。 关键词理解: "参加反应":只计算实际参与反应的物质,过量未反应的不计入 "质量总和":包括所有状态 (固、液、气) 的反应物和生成物质量 "等于":反应前后总质量严格相等,是质量守恒的核心 二、质量守恒定律的微观本质 化学反应前后,原子的 "三不变": 原子种类不变:反应前后元素种类不变 原子数目不变:反应前后各元素原子总数相等 原子质量不变:单个原子质量在反应中保持恒定 原因:化学反应本质是原子重新组合,原子是化学变化中最小微粒,既不产生也不消失,只是重新排列组合成新物质 三、化学反应前后的 "变" 与 "不变" 类别 一定不变 一定改变 可能改变 宏观 物质总质量 元素种类 元素质量 物质种类 分子总数 微观 原子种类 原子数目 原子质量 分子种类 元素化合价 四、质量守恒定律的实验验证 1. 红磷燃烧实验 实验装置:锥形瓶内放红磷,瓶塞上插玻璃管并套气球,放在天平上称量。 实验现象: 红磷燃烧,产生大量白烟 冷却后,天平仍保持平衡 结论:参加反应的红磷和氧气质量总和 = 生成的五氧化二磷质量 2. 铁钉与硫酸铜溶液反应 实验装置:烧杯中放硫酸铜溶液,加入铁钉,称量总质量。 实验现象: 铁钉表面覆盖一层红色物质 (铜) 溶液颜色由蓝色逐渐变浅 天平保持平衡 结论:参加反应的铁和硫酸铜质量总和 = 生成的铜和硫酸亚铁质量总和 3. 碳酸钠与盐酸反应 (密闭系统) 注意:若在开放容器中进行,生成的二氧化碳气体会逸出,导致反应后质量减小,看似不守恒。但在密闭容器中,反应前后质量相等,验证了质量守恒定律。 五、质量守恒定律的应用 1. 计算物质质量 例:A + B → C + D,已知 12g A 与 18g B 恰好完全反应,生成 28g C,求 D 的质量。 解:根据质量守恒定律,参加反应的 A 和 B 总质量 = 生成的 C 和 D 总质量12g + 18g = 28g + m (D)m (D) = 30g - 28g = 2g 2. 推断未知物质的化学式 例:某物质 R 燃烧:R + 3O₂ → 2CO₂ + 3H₂O,推断 R 的化学式。 解: 反应后 C 原子数:2,H 原子数:6,O 原子数:7 反应前 O₂提供 O 原子数:6 所以 R 中必含 C:2 个,H:6 个,O:1 个 R 化学式为 C₂H₆O (乙醇) 3. 混合物纯度计算 公式: 物质纯度 = 纯物质质量 / 混合物总质量 × 100% 纯物质质量 = 混合物总质量 × 纯度 混合物总质量 = 纯物质质量 ÷ 纯度 六、质量守恒定律的注意事项 仅适用于化学变化,不适用于物理变化 (如冰融化成水) 是质量守恒,不是体积守恒 (如 2 体积 H₂和 1 体积 O₂反应生成 2 体积 H₂O,体积不守恒) 计算时必须包括所有物质,特别是气体 (如燃烧反应中的氧气和生成的二氧化碳) 开放系统中,若有气体参与或生成,质量变化可能不明显,需在密闭系统中验证 七、总结 质量守恒定律是化学反应的基本规律,揭示了化学反应前后物质质量关系的本质。它不仅是化学方程式计算的理论基础,也为我们理解物质转化提供了定量视角。通过宏观质量测量和微观原子分析的结合,我们可以更深入地认识化学变化的本质 —— 原子的重新组合。 核心要点: 质量守恒定律内容:参加反应的各物质质量总和 = 生成的各物质质量总和 微观本质:反应前后原子的种类、数目、质量不变 应用:计算物质质量、推断化学式、纯度计算等
▶
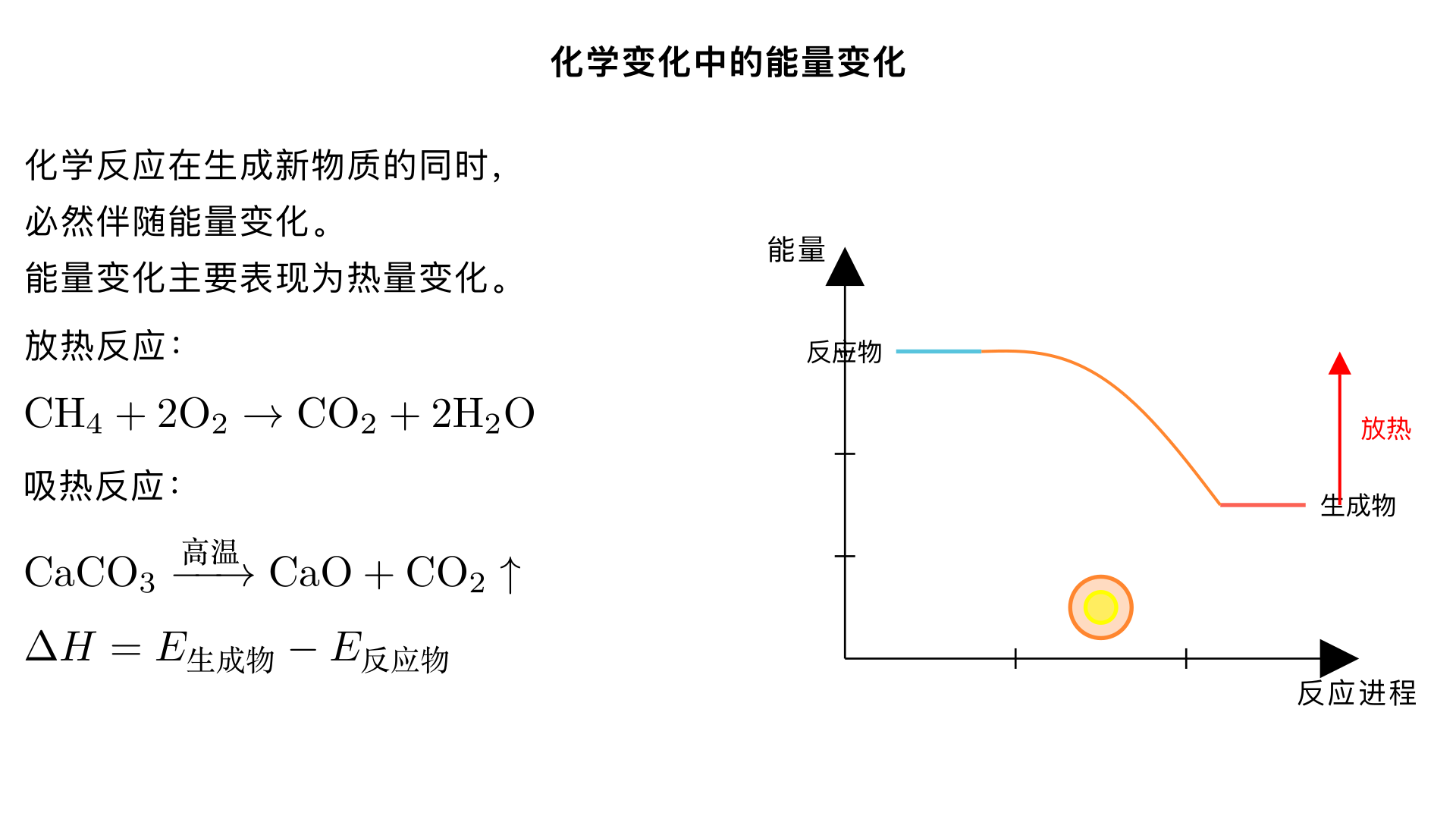
化学变化中的能量变化 一、化学反应中的能量变化概述 基本特征:任何化学反应在生成新物质的同时,都伴随着能量变化,通常表现为热量变化(吸热或放热),也可能有光能、电能等其他形式的能量变化。 能量守恒:在化学反应中,能量不能被创造或消灭,只能从一种形式转化为另一种形式。反应物总能量与生成物总能量的差值决定了反应是吸热还是放热。 二、放热反应与吸热反应 1. 放热反应 定义:化学反应过程中放出热量的反应,表现为体系温度升高。 微观本质:反应物总能量 > 生成物总能量,多余能量以热能形式释放。 常见类型: 所有燃烧反应(如甲烷燃烧:CH₄+2O₂→CO₂+2H₂O) 金属与酸反应(如锌与稀硫酸:Zn+H₂SO₄→ZnSO₄+H₂↑) 中和反应(酸与碱反应) 生石灰与水反应:CaO+H₂O→Ca (OH)₂(自热火锅发热原理) 大多数化合反应 2. 吸热反应 定义:化学反应过程中吸收热量的反应,表现为体系温度降低。 微观本质:反应物总能量 < 生成物总能量,需要从外界吸收能量。 常见类型: 需要持续加热或高温条件的反应(如碳与二氧化碳反应:C+CO₂高温→2CO) 大多数分解反应(如碳酸钙分解:CaCO₃高温→CaO+CO₂↑) 氢氧化钡晶体与氯化铵晶体反应(实验:混合物糊状,杯底玻璃片结冰) 部分溶解过程(如硝酸铵溶于水,溶液温度显著降低) 三、化学反应能量变化的微观本质 化学键的断裂与形成是化学反应中能量变化的主要原因。 过程 能量变化 实例 化学键断裂 吸收能量 反应物分子中的旧键断裂,需提供能量 化学键形成 释放能量 生成物分子中新键形成,释放能量 能量差决定反应类型: 若断键吸收的能量 < 成键释放的能量 → 放热反应(ΔH<0) 若断键吸收的能量 > 成键释放的能量 → 吸热反应(ΔH>0) 四、能量变化的应用 1. 化学能→热能 燃烧供热:家庭燃气、工业锅炉、火力发电(煤燃烧→水蒸汽→汽轮机→发电) 自热食品:发热包含生石灰 (CaO),与水反应放热 2. 化学能→电能 原电池:如干电池、蓄电池(化学能→电能) 例:铜锌原电池(Zn+2H⁺→Zn²⁺+H₂↑),电子通过导线产生电流 新型电池:锂电池(广泛用于手机、电脑)、氢氧燃料电池 3. 电能→化学能 电解水:2H₂O 通电→2H₂↑+O₂↑(电能→化学能) 工业冶炼:电解熔融氧化铝制铝、电解饱和食盐水制烧碱 五、判断放热 / 吸热反应的方法 观察温度变化:反应后温度升高→放热;温度降低→吸热 看反应条件: 需持续加热或高温→吸热反应 常温自发或点燃后持续进行→放热反应 能量关系判断: 反应物总能量 > 生成物总能量→放热反应 反应物总能量 < 生成物总能量→吸热反应 记忆常见类型: 放热:燃烧、金属与酸、中和、生石灰与水 吸热:高温分解、C+CO₂、Ba (OH)₂・8H₂O+NH₄Cl 六、总结与应用 核心要点: 化学反应必伴随能量变化,主要表现为热量变化 能量变化源于化学键的断裂与形成的能量差 放热反应(如燃烧)释放能量供人类利用;吸热反应(如工业高温合成)需外部能量支持 应用意义:理解化学反应中的能量变化,有助于我们合理利用能源(如选择高效清洁燃料)、控制反应条件(提高产率、保障安全)、开发新能源(如氢能源、新型电池),为解决能源危机和环境保护提供科学依据。
▶
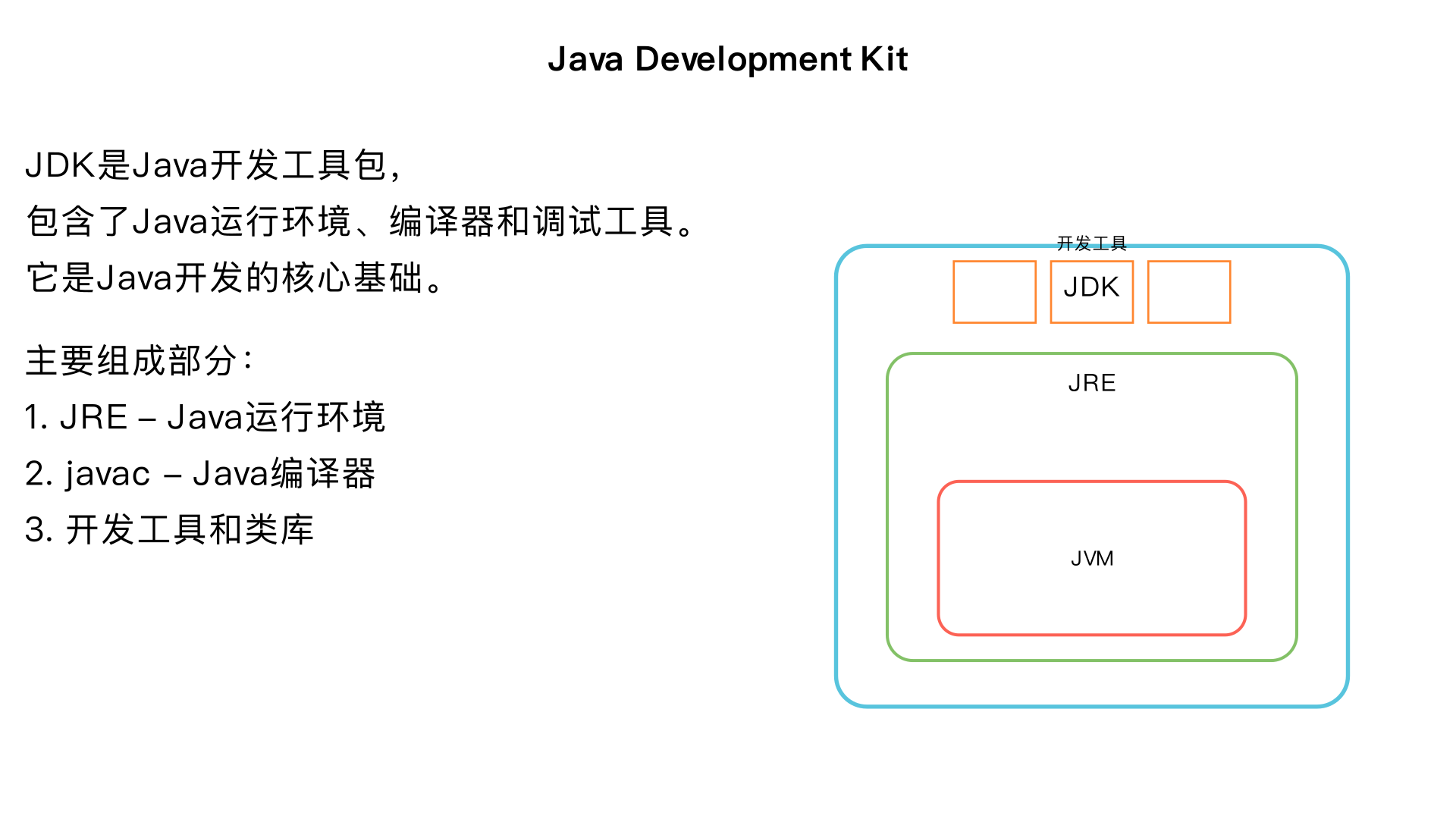
jdk
▶
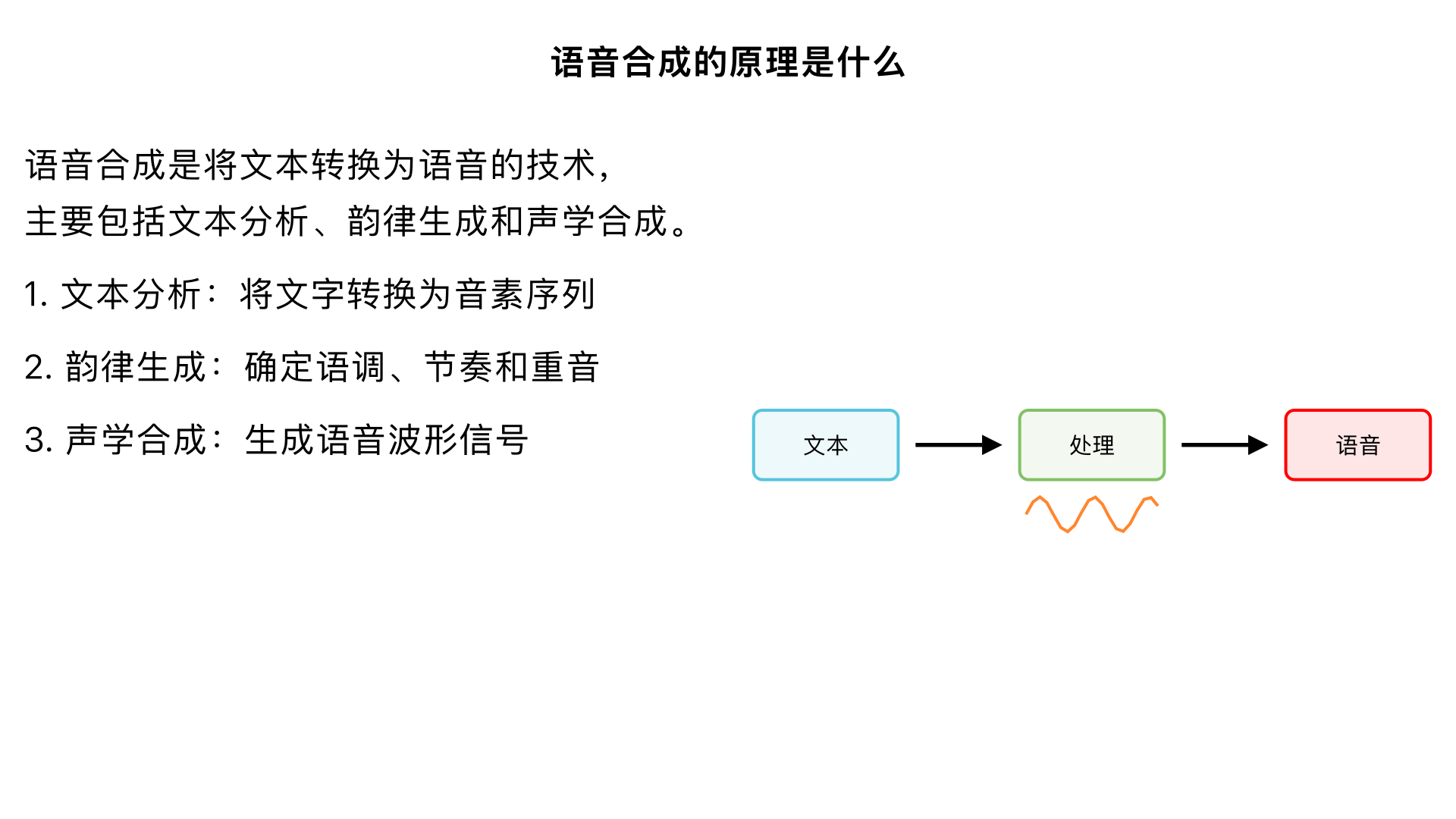
语言合成的原理是什么?
▶
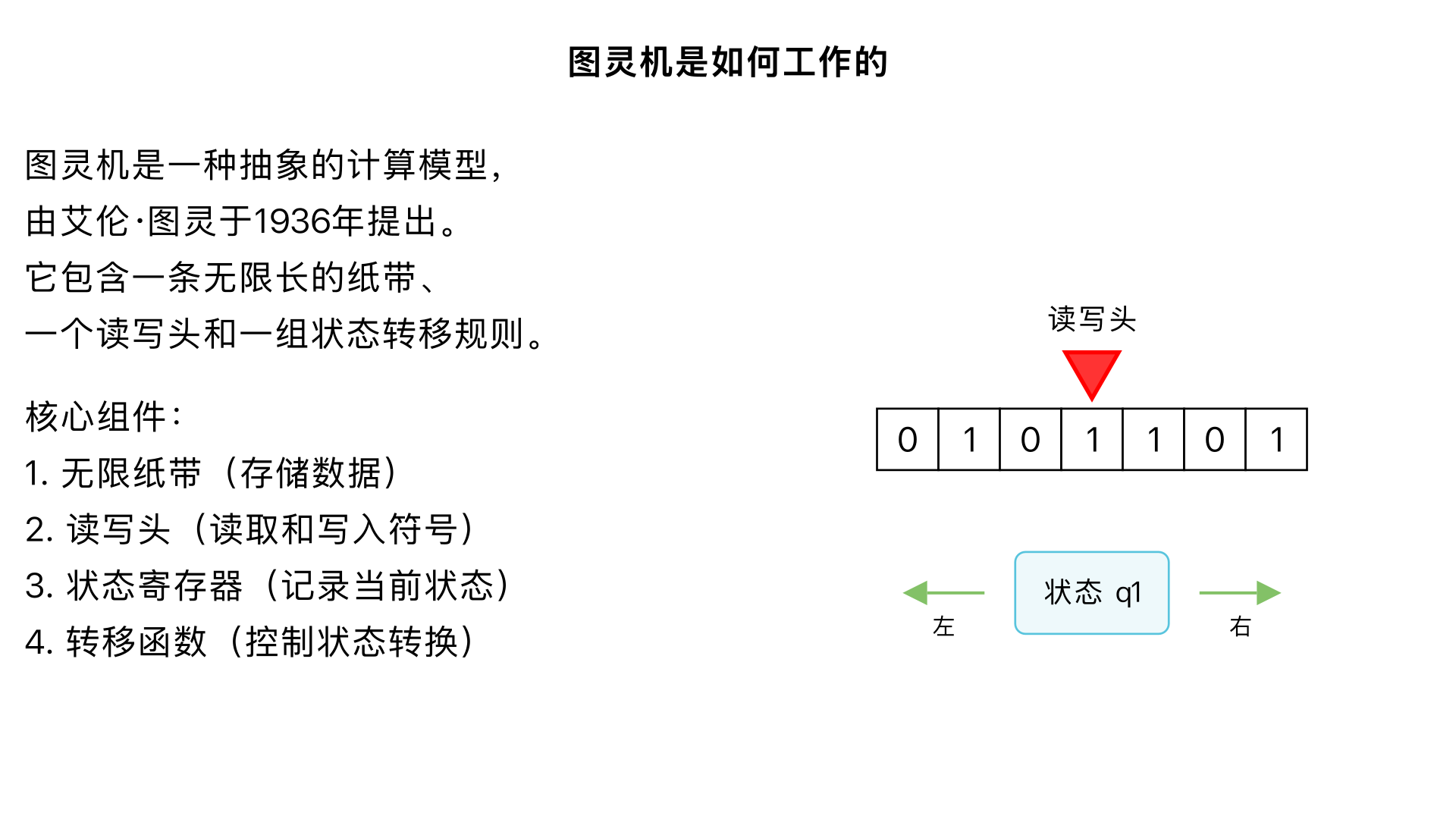
图灵机是如何工作的
▶
九年级化学 / 认识化学元素 / 化学式 一、化学式的定义 用元素符号和数字的组合来表示物质组成的式子,叫做化学式。 每种纯净物的组成是固定不变的,因此一种物质只有一个对应的化学式;混合物因组成不固定,没有专门的化学式。 例如:水的化学式为,氧气的化学式为,氯化钠的化学式为。 二、化学式表示的意义 化学式的意义分为宏观意义和微观意义,以为例: 宏观意义 表示一种物质:表示水这种物质。 表示物质的元素组成:表示水由氢元素和氧元素组成。 微观意义 表示物质的一个分子:表示一个水分子。 表示分子的构成:表示一个水分子由 2 个氢原子和 1 个氧原子构成。 注意:若化学式前加数字,只表示微观意义(粒子个数),如只表示2 个水分子,无宏观意义。 三、化学式的书写规则 1. 单质化学式的书写 金属单质、固态非金属单质(碘除外)、稀有气体:直接用元素符号表示。 例:铁、碳、氦气。 气态非金属单质(双原子分子):在元素符号右下角标注数字 “2”。 例:氧气、氢气、氮气、氯气。 2. 化合物化学式的书写 (1)原则 正价元素(或原子团)写在左边,负价元素(或原子团)写在右边。 化合物中各元素正负化合价的代数和为 0(化合价规则)。 (2)步骤(以书写氧化铝的化学式为例) 写出组成元素的符号:正价铝在左,负价氧在右; 标注元素化合价:、; 交叉化合价绝对值,标注原子个数:铝的化合价绝对值 “3” 写在氧右下角,氧的化合价绝对值 “2” 写在铝右下角,得到; 检验: (+3)×2+(−2)×3=0 ,符合化合价代数和为 0 的规则,化学式正确。 (3)含原子团的化合物 原子团作为整体参与书写,若原子团个数大于 1,需给原子团加括号,再标注数字。 例:氢氧化钙中,钙为 +2 价,氢氧根为 −1 价,化学式为;硫酸铝中,铝为 +3 价,硫酸根为 −2 价,化学式为。 四、化学式的读法 1. 单质 金属、固态非金属、稀有气体:直接读元素名称,如读铁,读氦气。 气态非金属单质:一般读 “某气”,如读氧气,读氢气。 2. 化合物 两种元素组成的化合物:一般读作 “某化某”,若元素有多种化合价,需读出原子个数。 例:读氯化钠,读一氧化碳,读二氧化碳,读氧化铁(或三氧化二铁),读氧化亚铁。 含原子团的化合物: 含氢氧根():读作 “氢氧化某”,如读氢氧化钠,读氢氧化钙。 含酸根(如、、):读作 “某酸某”,如读硫酸钠,读碳酸钙,读硝酸钾;含的化合物,读作 “某化铵” 或 “某酸铵”,如读氯化铵,读硫酸铵。 五、化学式相关计算(基础) 计算相对分子质量:化学式中各原子的相对原子质量的总和。 例:的相对分子质量 =1×2+16=18 。 计算元素质量比:化合物中各元素的相对原子质量 × 原子个数之比。 例:中氢、氧元素质量比 =(1×2):16=1:8 。 计算元素质量分数:某元素的质量分数 该 元 素 相 对 原 子 质 量 原 子 个 数 化 合 物 相 对 分 子 质 量 。 例:中氢元素质量分数 = 18 1×2 ×100%≈11.1% 。
▶
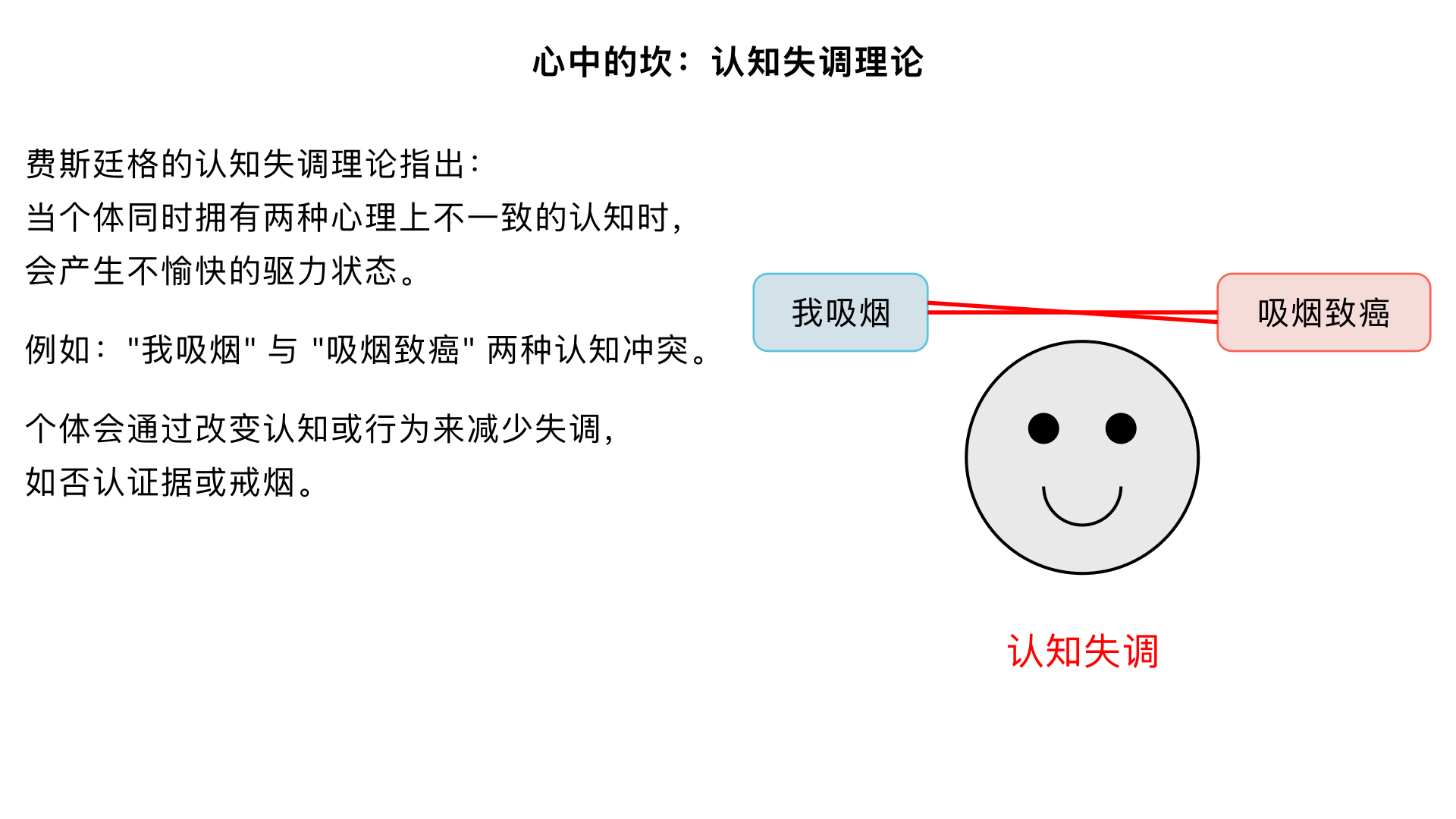
心中的坎 (费斯廷格的“认知失调”理论) 主要内容:提出当个体同时拥有两种在心理上不一致的认知(如“我吸烟”和“吸烟致癌”)时,会产生一种不愉快的驱力状态(认知失调),促使个体改变认知或行为来减少失调(如否认证据、戒烟)。
▶
七年级数学 / 实数 / 立方根 一、立方根的基本定义 如果一个数的立方等于 a ,那么这个数就叫做 a 的立方根,也叫做 a 的三次方根。 数学表达式:若 x 3 =a ,则 x 叫做 a 的立方根,记作 x= 3 a ,其中符号 “ 3 ” 称为三次根号, a 是被开方数,根指数 3 不能省略(平方根的根指数 2 可省略)。 示例:因为 2 3 =8 ,所以 8 的立方根是 2 ,即 3 8 =2 ;因为 (−2) 3 =−8 ,所以 −8 的立方根是 −2 ,即 3 −8 =−2 。 二、立方根的核心性质 唯一性:任何实数都有且只有一个立方根。 与平方根不同(负数没有平方根),正数、负数、 0 都能找到唯一的立方根。 符号性: 正数的立方根是正数,例如 3 27 =3 ; 负数的立方根是负数,例如 3 −64 =−4 ; 0 的立方根是 0 ,即 3 0 =0 。 特殊等式: 3 −a =− 3 a ,即负数的立方根可转化为其相反数的立方根的相反数,比如 3 −125 =− 3 125 =−5 。 三、立方根的计算方法 开立方与立方互为逆运算:求一个数的立方根,可通过找哪个数的立方等于被开方数来确定。 示例:求 3 64 ,因为 4 3 =64 ,所以 3 64 =4 ;求 3 − 8 1 ,因为 (− 2 1 ) 3 =− 8 1 ,所以 3 − 8 1 =− 2 1 。 常见立方根数值(需熟记): 被开方数 a 3 a 被开方数 a 3 a 0 0 −1 −1 1 1 −8 −2 8 2 −27 −3 27 3 −64 −4 64 4 −125 −5 四、立方根与平方根的区别 对比维度 平方根 立方根 存在范围 非负数才有平方根 全体实数都有立方根 个数 正数有两个互为相反数的平方根, 0 的平方根是 0 任何实数都只有一个立方根 符号 正数的平方根一正一负 正数立方根为正,负数立方根为负 根指数 根指数 2 可省略 根指数 3 不可省略 五、立方根的简单应用 利用立方根可解决与体积相关的实际问题,比如求正方体的棱长。 示例:一个正方体的体积为 216 立方厘米,求其棱长。设棱长为 x 厘米,则 x 3 =216 ,解得 x= 3 216 =6 ,即棱长为 6 厘米。
▶