T
Teach Me AnythingTMA
Video History
Page 32 / 44
▶
Set up a generating function and use it to find the number of ways in which nine identical blocks can be given to four children if each child gets at least one block.
![3. Solve the recurrence relation
\[
a_n = 2a_{n-1}
\]
using generating functions. Where \( a_0 = 1 \)
*Note:* *I won’t ask a harder one than this if specifically requesting generating functions to solve a recurrence.*
注意公式使用 mathtex](https://manimvideo.explanation.fun/video/cover/578398786136838145.png)
▶
3. Solve the recurrence relation \[ a_n = 2a_{n-1} \] using generating functions. Where \( a_0 = 1 \) *Note:* *I won’t ask a harder one than this if specifically requesting generating functions to solve a recurrence.* 注意公式使用 mathtex
▶
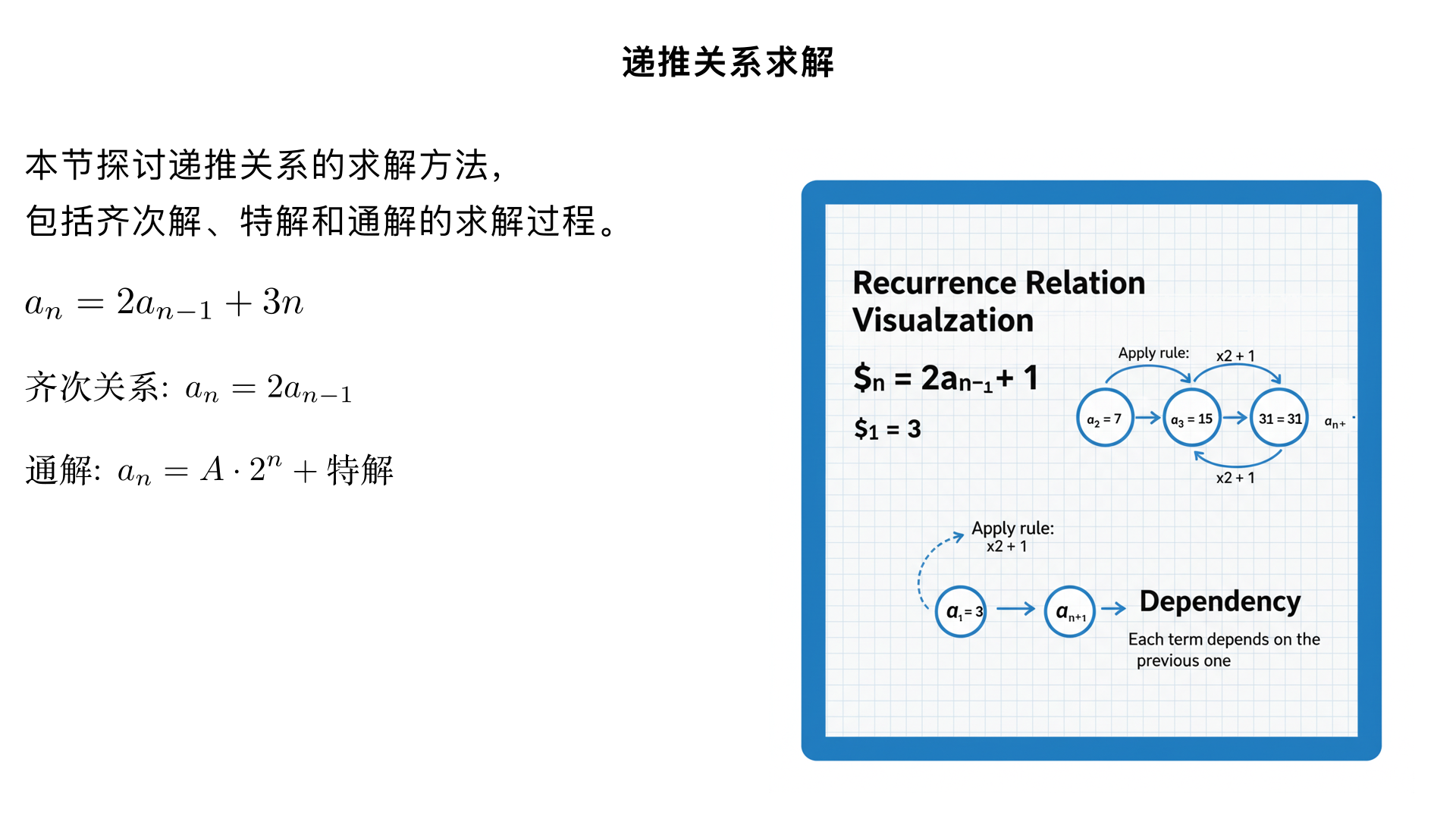
### 2. Consider the recurrence relation ( a_n = 2a_{n-1} + 3n ) **(a)** Write the associated homogeneous recurrence relation. --- **(b)** Find the general solution to the associated homogeneous recurrence relation. --- **(c)** Find the particular solution to the given recurrence relation. --- **(d)** Give the general solution to the given recurrence relation. --- **(e)** Find the solution to the given recurrence relation when ( a_0 = 1 )

▶
在一个式子中,什么是项
▶
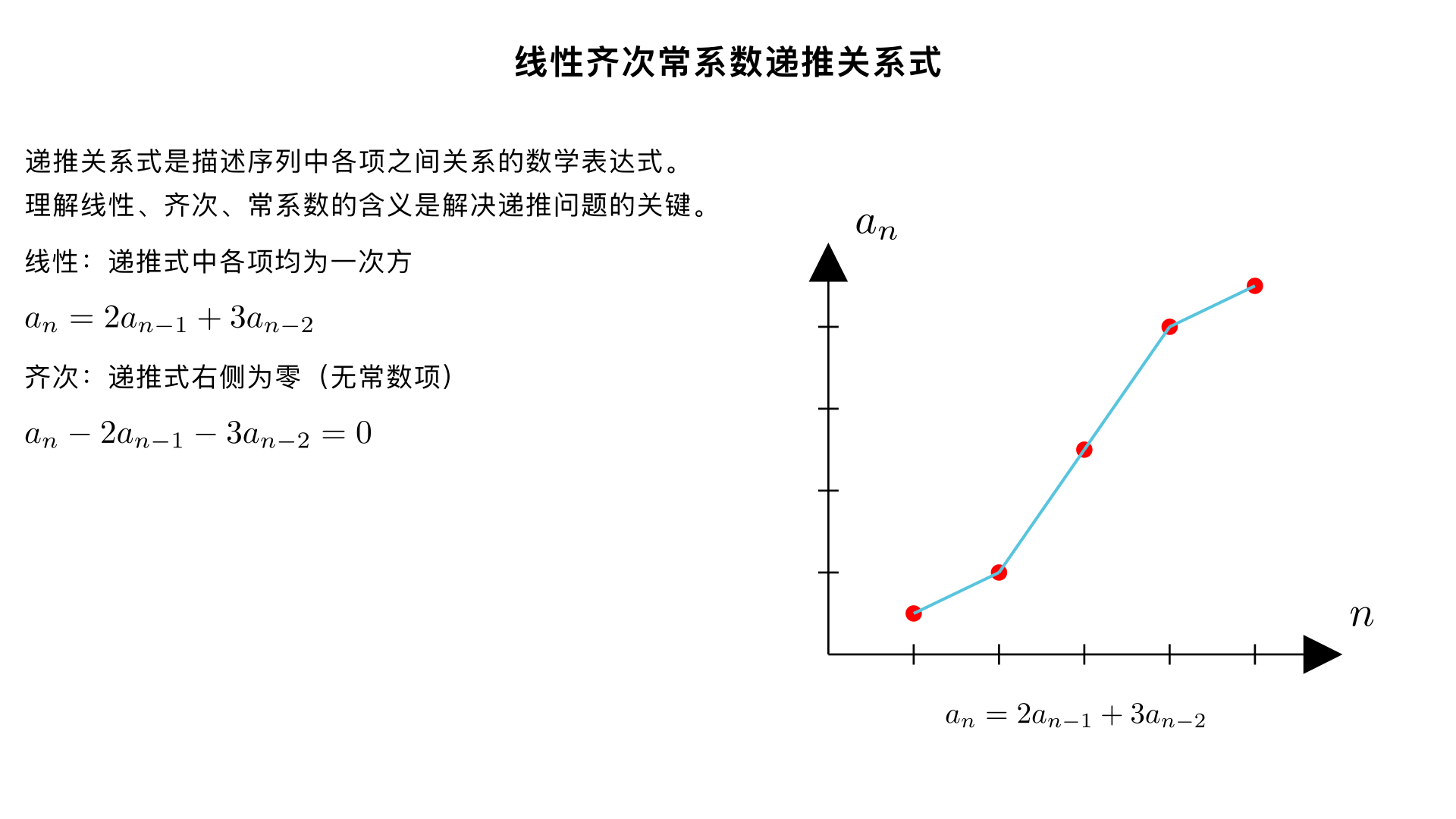
线性齐次常系数递推关系式 什么是线性,什么是齐次
▶
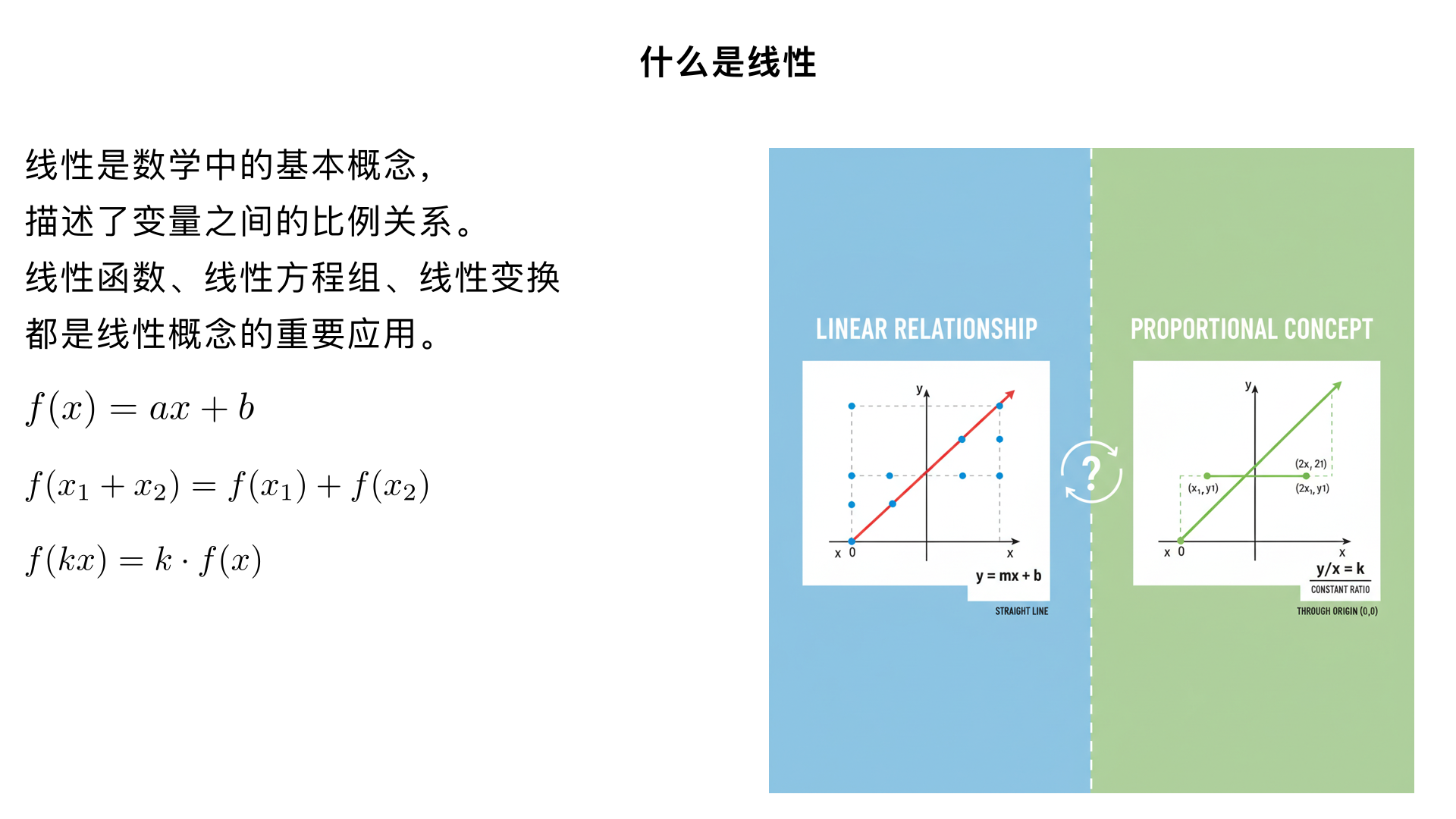
什么时线性
▶
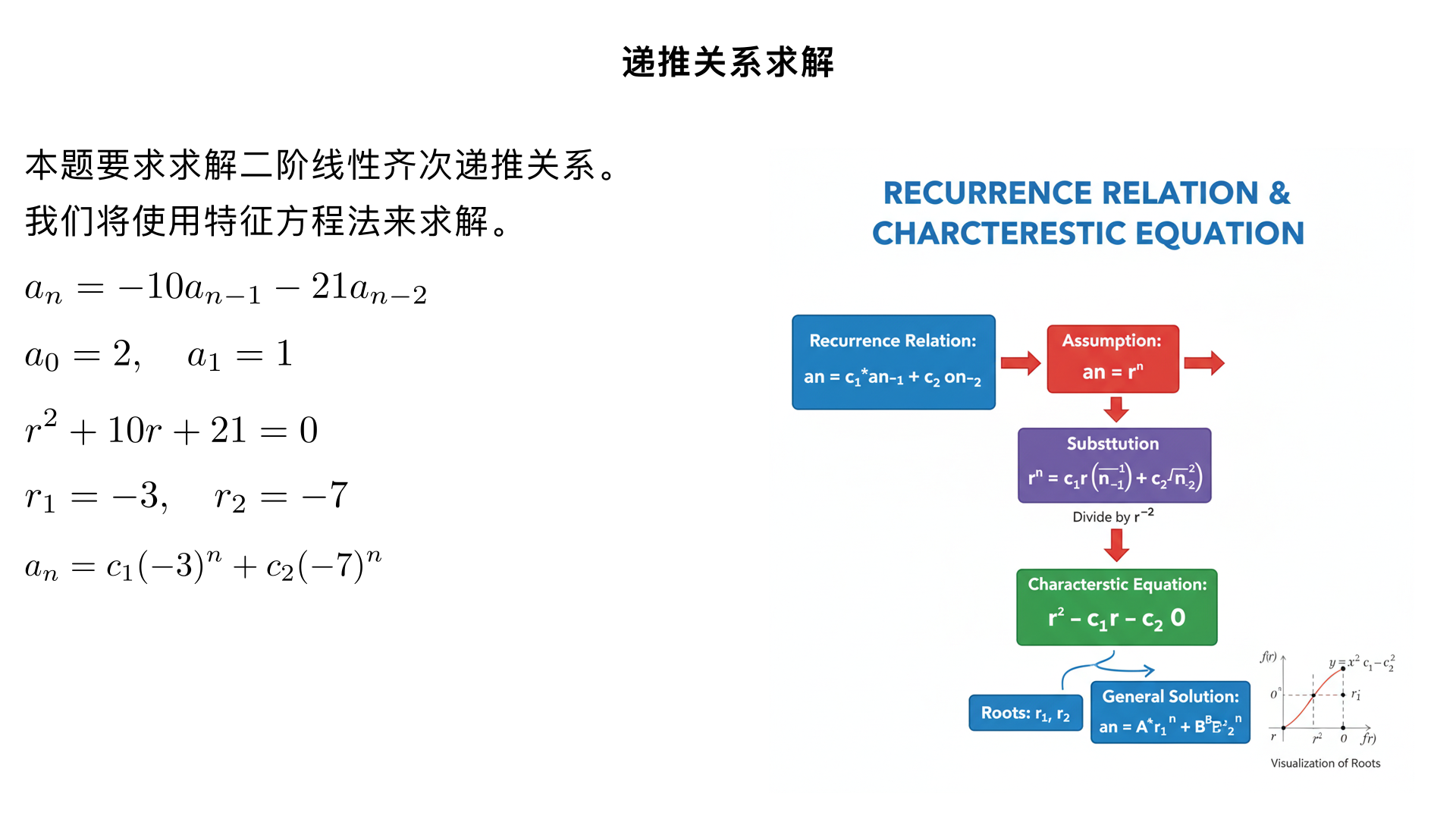
Solve this recurrence relation using any method learned in class: aₙ = -10aₙ₋₁ - 21aₙ₋₂ where: a₀ = 2, a₁ = 1.
▶
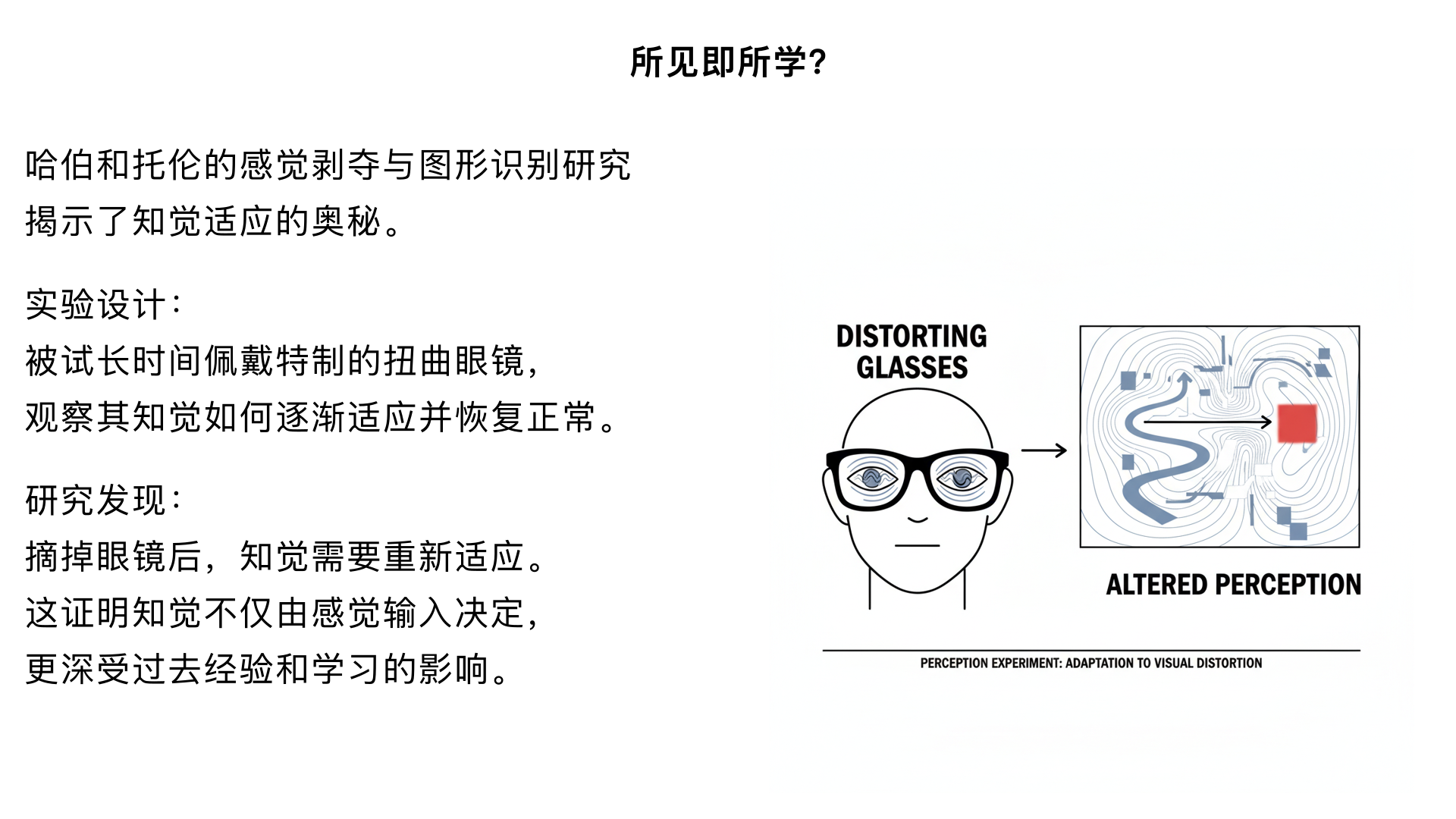
所见即所学? (哈伯和托伦的“感觉剥夺与图形识别”研究) 主要内容:让被试长时间佩戴特制的 distorting 眼镜,发现其知觉逐渐适应并恢复正常。但当摘掉眼镜后,其知觉又需要重新适应。这证明知觉不仅由感觉输入决定,更深受过去经验和学习的影响。
▶
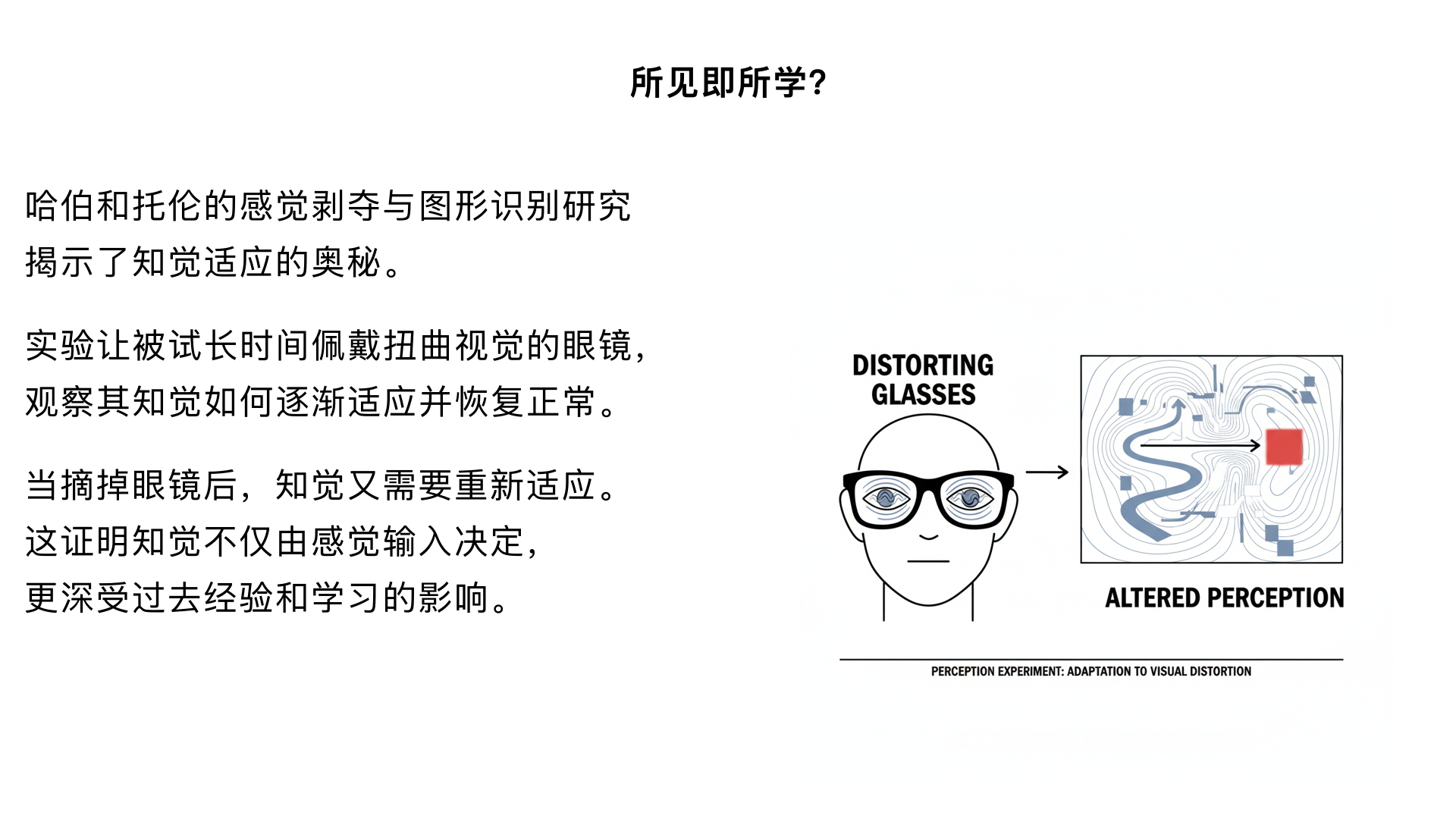
5、所见即所学? (哈伯和托伦的“感觉剥夺与图形识别”研究) 主要内容:让被试长时间佩戴特制的 distorting 眼镜,发现其知觉逐渐适应并恢复正常。但当摘掉眼镜后,其知觉又需要重新适应。这证明知觉不仅由感觉输入决定,更深受过去经验和学习的影响。

▶
第9课:《易经》的运用——占卜的原则与方法 主要内容: 占卜的哲学基础:“寂然不动,感而遂通”。 占卜的三原则:不诚不占、不义不占、不疑不占。 介绍傅佩荣老师推荐的“数字占卜法”(简单、易行、无需道具)。

▶
4、小心视崖! (吉布森和沃克的“视崖”研究) 主要内容:通过设计一个看似有“悬崖”的玻璃桌面(“视崖”),观察婴儿是否会拒绝爬过“深侧”。研究发现,大部分六个月以上的婴儿会表现出对深侧的恐惧,这表明深度知觉可能在人类开始爬行时就已具备,这为先天论提供了支持。

▶