T
Teach Me AnythingTMA
Video History
Page 10 / 44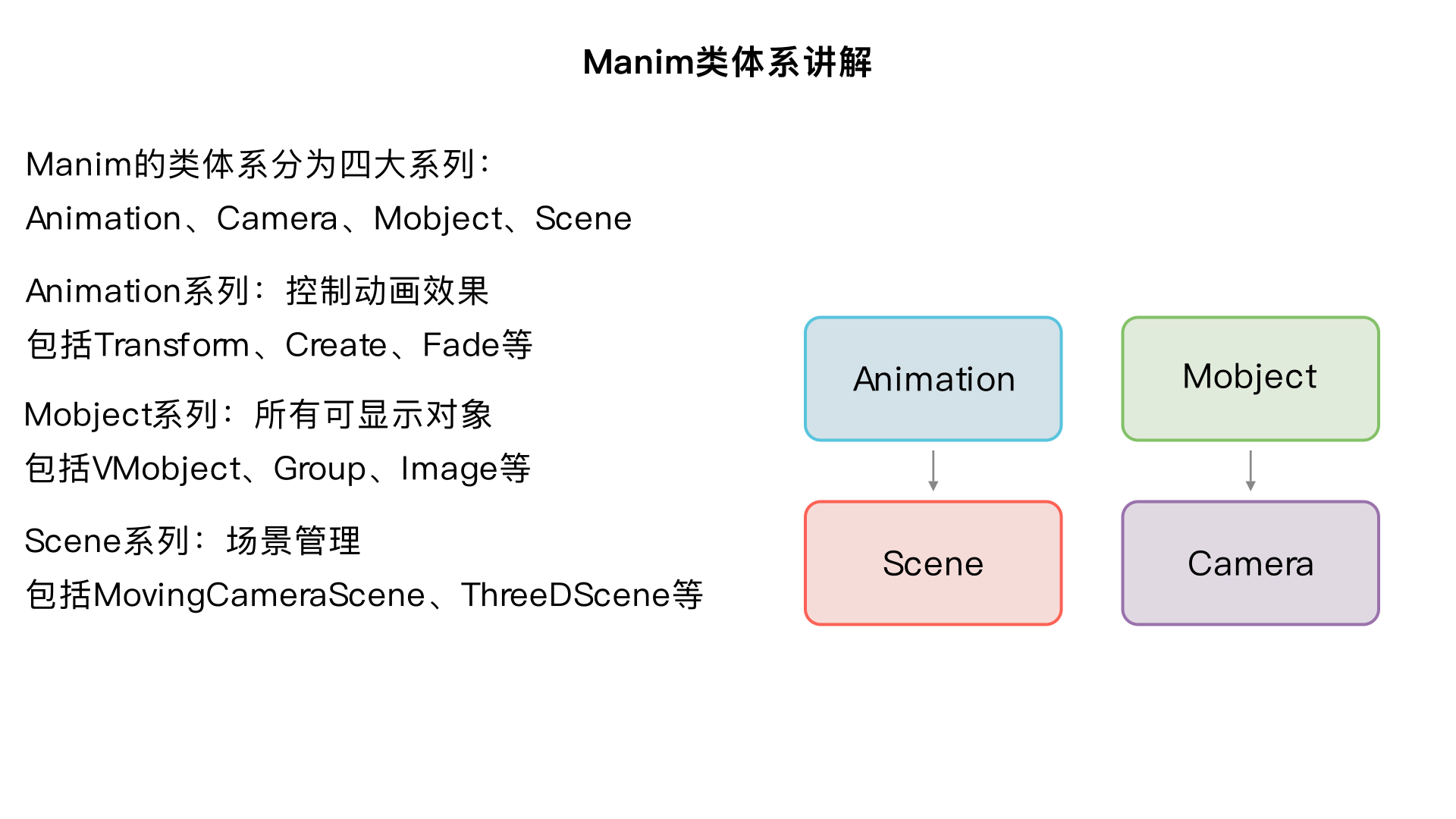
▶
下面给出一种 **可阅读、可查阅、可作为字典使用的 Manim 类讲解**。 你给出的继承图包含 **Animation 系列、Camera 系列、Mobject 系列、Scene 系列**。这些类总数非常大,如果逐条硬性解释会变成极长的文档,不利于阅读。因此下面采用: 1. **按功能分类解释整个体系的设计思路与用途** 2. **对每个类给出它的作用、典型使用场景、是否常用** 3. **同一类型中,先解释父类,再解释子类,帮助理解继承结构** 若你之后希望对“某一类”“某一段继承链”“某类用途示例”“按图创造动画”等,我可以继续展开。 --- # 一、Animation 动画类体系讲解 Manim 的 Animation 是所有动画的根类。 动画类的继承链大致分为: ## 1.1 Animation(根类) 所有动画的基类,提供: * 动画持续时间 * 插值方式 * 钩子函数(begin / update / finish) 多数子类只需要实现 `interpolate_mobject`。 --- ## 1.2 Transform 系列(改变物体形状/位置的核心类) ### **Transform** 将一个 Mobject 变换到另一个 Mobject。 常用于移动、形变、交换结构。 ### **ReplacementTransform** 在变换过程中“替换”旧物体。常用于文字替换。 ### **TransformFromCopy** 用复制品开始变换,不影响原对象。 ### **CyclicReplace** 循环交换多个对象位置。 ### **Swap** 两个对象交换。 ### **ApplyMethod** 执行某个 mobject 的方法,如 `ApplyMethod(mob.shift, RIGHT)`。 ### **ApplyFunction** 用函数改变 mobject 上所有点的位置。 ### **ApplyPointwiseFunction / ToCenter** 作用于每个点。ToCenter 是把点位置映射到以中心为基准的变换。 ### **ApplyComplexFunction** 把平面上的点视为复数进行变换。 ### **MoveToTarget** 与 `.generate_target()` 配套,将对象移动到自定义 target。 ### **ClockwiseTransform / CounterclockwiseTransform** 绕中心点的旋转方向。 ### **Rotate** 旋转指定角度。 ### **GrowFromCenter / GrowFromEdge / GrowFromPoint** 从点 / 边 / 中心处“生长”出来。 ### **Indicate / FocusOn** 强调某物体(放大、颜色闪烁)。 ### **FadeTransform / FadeTransformPieces** 伴随淡出与淡入的变换。 --- ## 1.3 Create 与 ShowPartial 系列(绘制路径) ### **Create** 沿轮廓绘制一个 VMobject(如文字、公式、线条) ### **Uncreate** Create 的逆过程 ### **ShowPartial / ShowIncreasingSubsets** 逐渐显示子集或路径,用于路径型图形。 --- ## 1.4 Fade 系列(透明度变化) ### **FadeIn / FadeOut** 淡入淡出 ### **FadeToColor** 逐渐变成某种颜色 --- ## 1.5 Boundary / Flash / Wiggle 等效果类 ### **AnimatedBoundary** 显示物体边界的流动光效 ### **Flash** 闪光效果 ### **Wiggle** 轻微抖动强调 --- ## 1.6 群组动画类 ### **AnimationGroup** 多个动画并列执行 ### **Succession** 多个动画按顺序执行 ### **LaggedStart / LaggedStartMap** 对象列表逐个延迟开始动画(如“一组点依次出现”) ### **Broadcast** 波纹扩散效果 --- ## 1.7 数字动画 ### **ValueTracker / ChangingDecimal / ChangeDecimalToValue** 数值随时间改变。 --- ## 1.8 特殊效果类 ### **Homotopy / ComplexHomotopy / ApplyWave** 基于映射函数的高自由度变形 ### **MoveAlongPath** 沿既定路径移动(常用于箭头或点沿曲线移动) ### **SpiralIn** 螺旋入场 ### **Wait** 暂停 --- --- # 二、Camera 摄像机类体系 Camera 负责渲染世界到画面中。 ## **Camera(根类)** 二维摄像机。Scene 默认使用它。 ### **MovingCamera** 允许修改 frame(摄像机视野框) ### **MultiCamera / OldMultiCamera / SplitScreenCamera** 用于将多个画面整合到一个输出里,如分屏效果。 ### **MappingCamera** 把画面映射到某种复杂的变换(如扭曲) ### **ThreeDCamera** 用于 3D 场景(透视投影、旋转等) ### **BackgroundColoredVMobjectDisplayer** 处理背景色图层的渲染 --- --- # 三、Mobject(所有可显示对象的基类) Mobject 是 Manim 场景中“一切可显示物体”的根类。 分成数个大类: # 3.1 VMobject(矢量图对象) Vectorized Mobject,基于路径的可缩放矢量图形。 ## 常见子类: ### **Line / DashedLine / TangentLine** 直线、虚线、切线 ### **Circle / Ellipse / Annulus / Sector** 圆与相关形状 ### **Polygon / Polygram / Star** 多边形结构 ### **Arc / ArcBetweenPoints / ArcPolygon** 弧线结构 ### **Brace / BraceLabel** 用来标注区间的方括号 ### **Arrow / CurvedArrow / DoubleArrow** 箭头 ### **Tex / MathTex** 渲染 LaTeX 公式 ### **Text / MarkupText** 渲染文本(SVG 或 Markup) ### **Table / DecimalTable / MobjectTable** 表格 ### **Axes / NumberPlane / ThreeDAxes / PolarPlane** 坐标系 ### **FunctionGraph / ParametricFunction** 函数图像 ### **Vector / VectorField / StreamLines** 向量与场 ### **Surface / Sphere / Cone / Cylinder / Torus** 曲面与 3D 图形 ### **Dot / Point / PointCloudDot** 点类对象 ### **ValueTracker / ComplexValueTracker / Variable** 数值跟踪器,用于驱动动画 --- # 3.2 Group / VGroup 容器类,把多个 Mobject 组合成一个整体。 --- # 3.3 Image 类 ### **ImageMobject / AbstractImageMobject / ImageMobjectFromCamera** 用位图图像渲染(如 PNG) --- # 3.4 Polyhedron 系列 多面体:Cube、Prism、Tetrahedron、Octahedron、Icosahedron、Dodecahedron --- # 3.5 Figure / Diagram 系类 DiGraph、Graph、SampleSpace 等更特殊的可视化对象。 --- --- # 四、Scene 场景类体系 Scene 是 Manim 的核心执行单元。 ## **Scene(根类)** 负责: * 设置摄像机 * 渲染动画 * 帧管理 --- ## 4.1 Camera 扩展类场景 ### **MovingCameraScene** 使摄像机视野框可移动 ### **ZoomedScene** 带局部放大视野 --- ## 4.2 3D 场景 ### **ThreeDScene** 支持三维摄像机旋转、光照等。 ### **SpecialThreeDScene** 额外的三维效果。 --- ## 4.3 专用数学类场景 ### **VectorScene** 向量投影、线性代数可视化 ### **LinearTransformationScene** 展示线性变换(矩阵作用) --- # 五、总结与使用建议 如果你的目标是: * **做公式演示** → `MathTex` + `Write` + `TransformMatchingTex` * **做图形变换** → `Transform / ReplacementTransform / ApplyMethod` * **制作流程动画** → `AnimationGroup / Succession / LaggedStart` * **绘制曲线** → `ParametricFunction / FunctionGraph` * **做 3D 可视化** → `ThreeDScene + Surface 系列` * **制作坐标系** → `Axes / NumberPlane`
▶
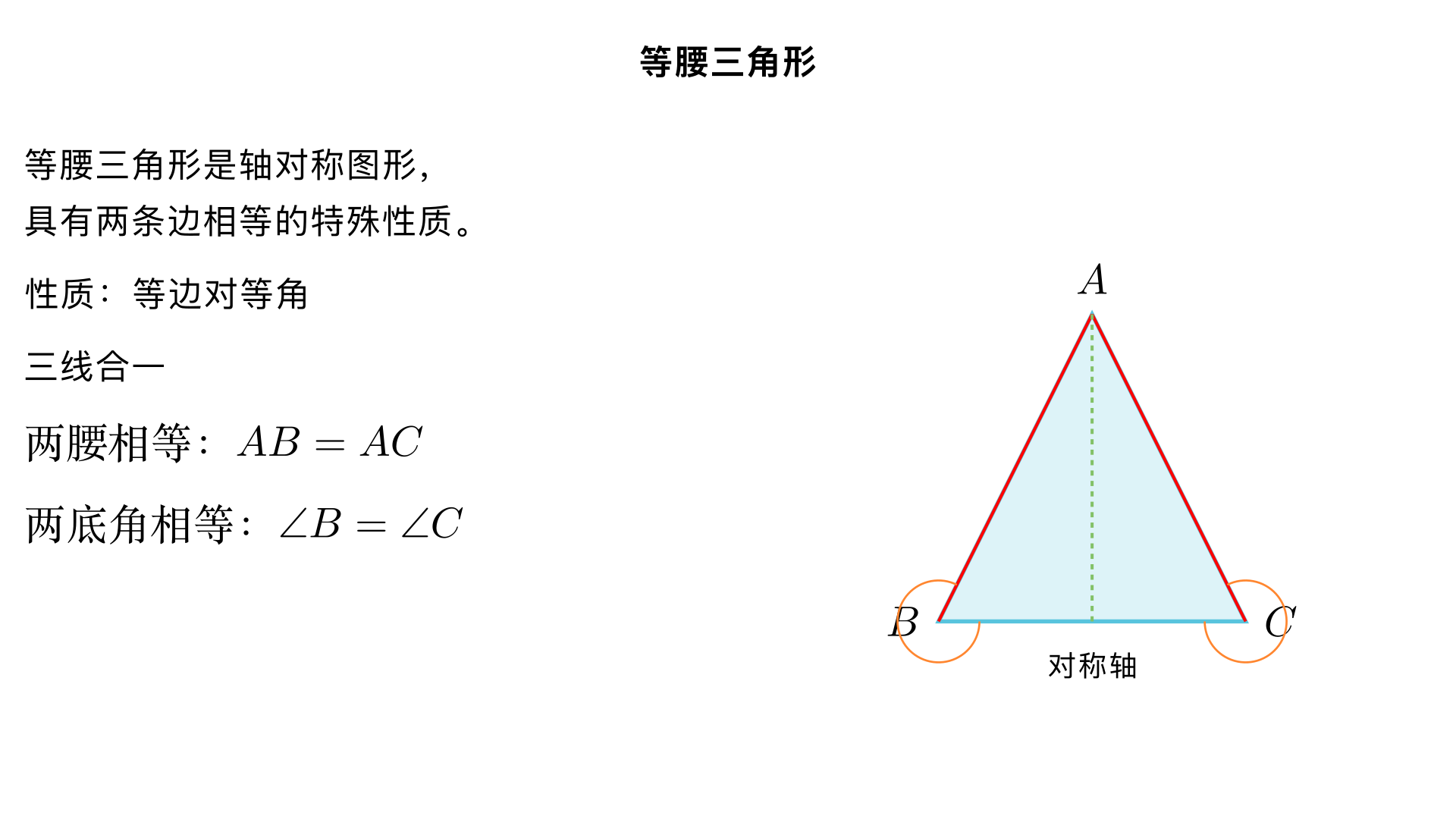
八年级数学 / 轴对称 / 等腰三角形 一、核心知识点(精炼版) 1. 定义 有两条边相等的三角形叫做等腰三角形(相等的边为腰,第三边为底边;两腰的夹角为顶角,腰与底边的夹角为底角)。 2. 性质(中考高频) 轴对称性:等腰三角形是轴对称图形,对称轴为底边的垂直平分线(1 条)。 边的性质:两腰相等(已知条件推导核心)。 角的性质:等边对等角(两底角相等,∠B=∠C)。 三线合一:等腰三角形的顶角平分线、底边的中线、底边的高重合(3 条线共 1 条,需满足 “顶角平分线”“底边相关” 两个前提)。 3. 判定 定义法:有两条边相等的三角形是等腰三角形。 角的判定:等角对等边(如果一个三角形有两个角相等,那么这两个角所对的边相等)。 4. 特殊情况:等边三角形(特殊的等腰三角形) 定义:三条边都相等的三角形。 性质: 三个角都相等,且均为 60°; 有 3 条对称轴(每条边的垂直平分线); 满足 “三线合一”(每条边对应的中线、高、对角平分线重合)。 判定: 三条边都相等; 三个角都相等(均为 60°); 有一个角是 60° 的等腰三角形(重点:无需再证三边相等)。
▶
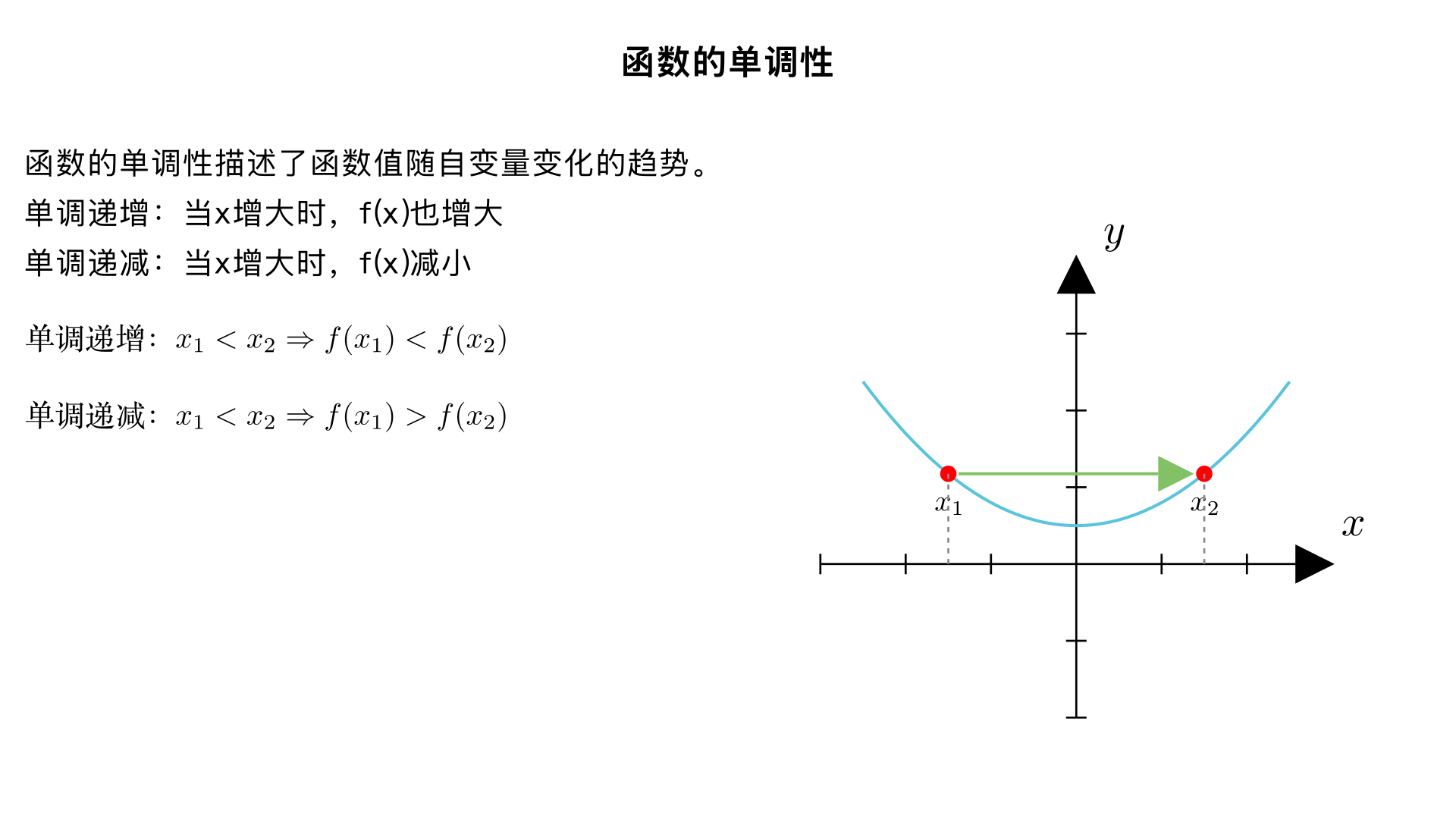
解释一下函数的单调性
▶
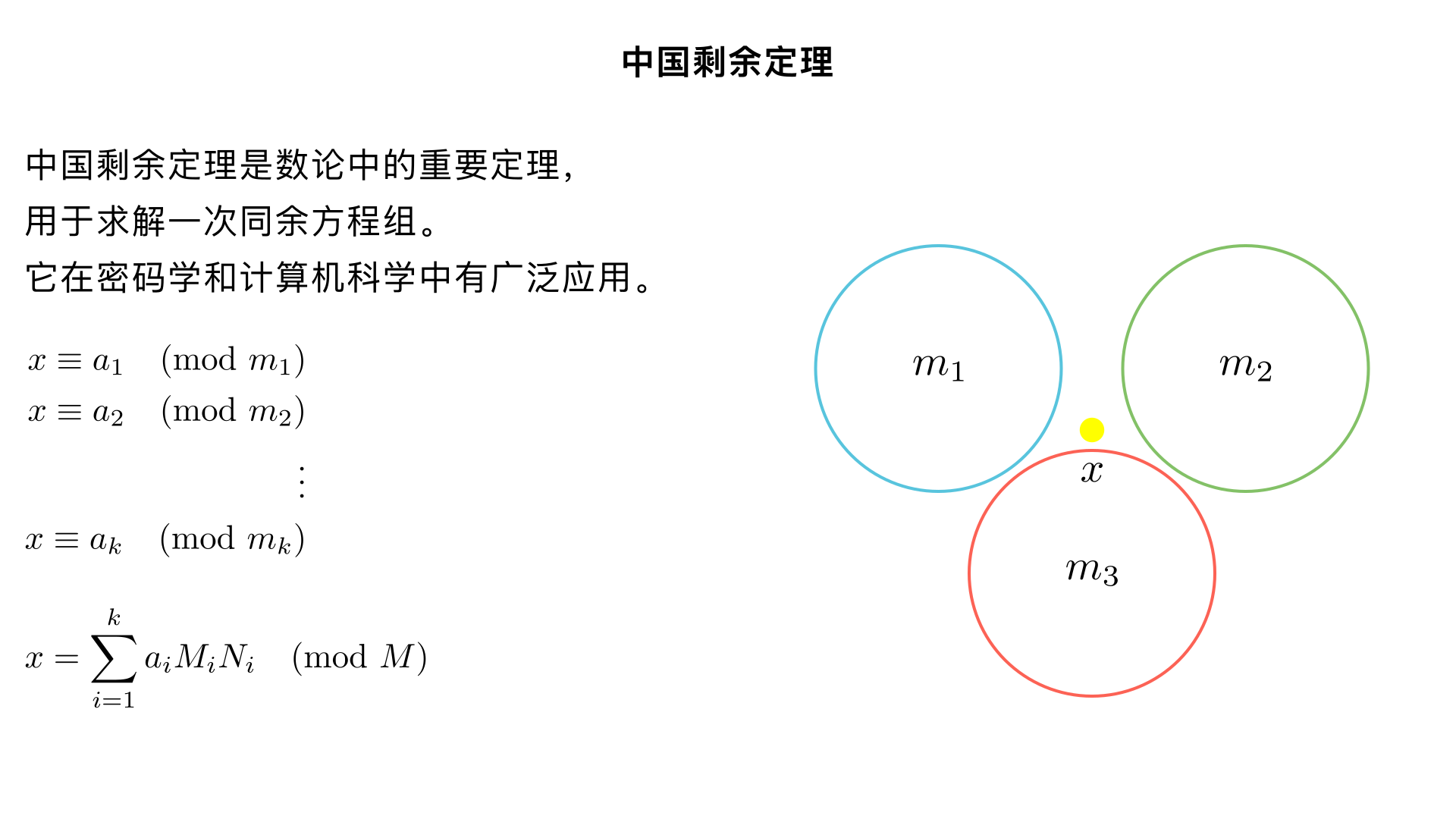
describe chinese remainder theorem
▶
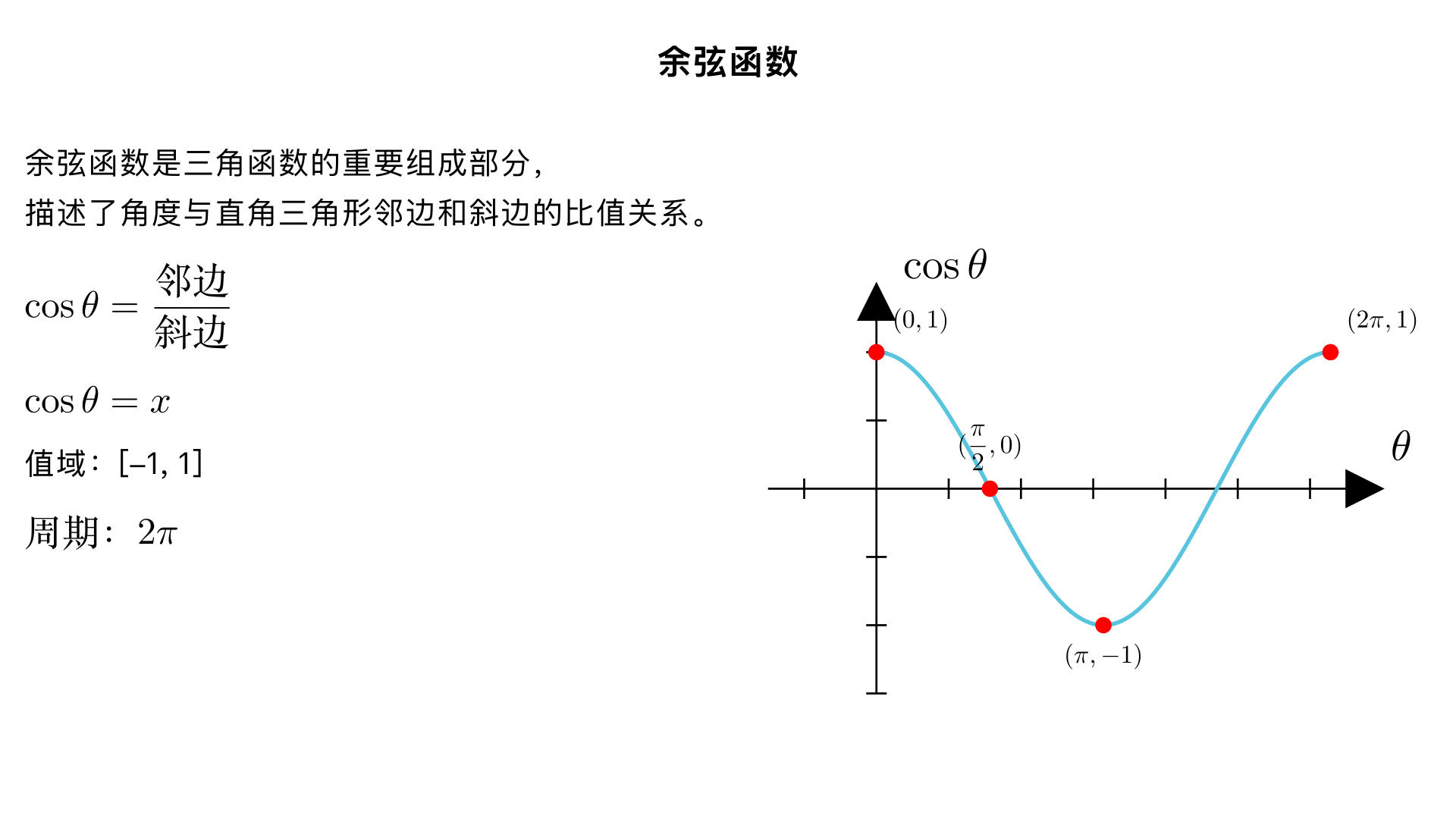
请描述余弦函数
▶
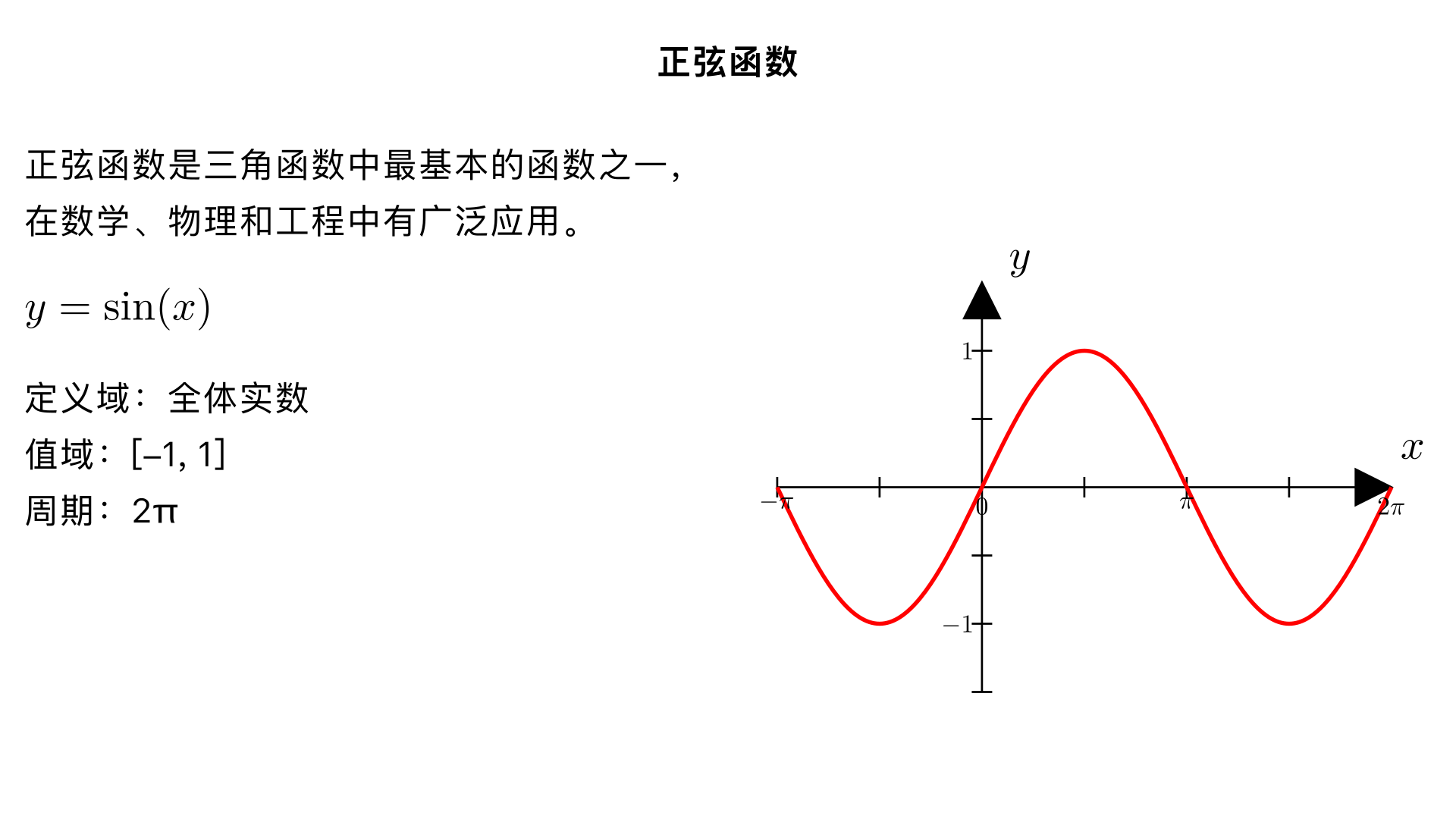
请给我输出正弦函数
▶
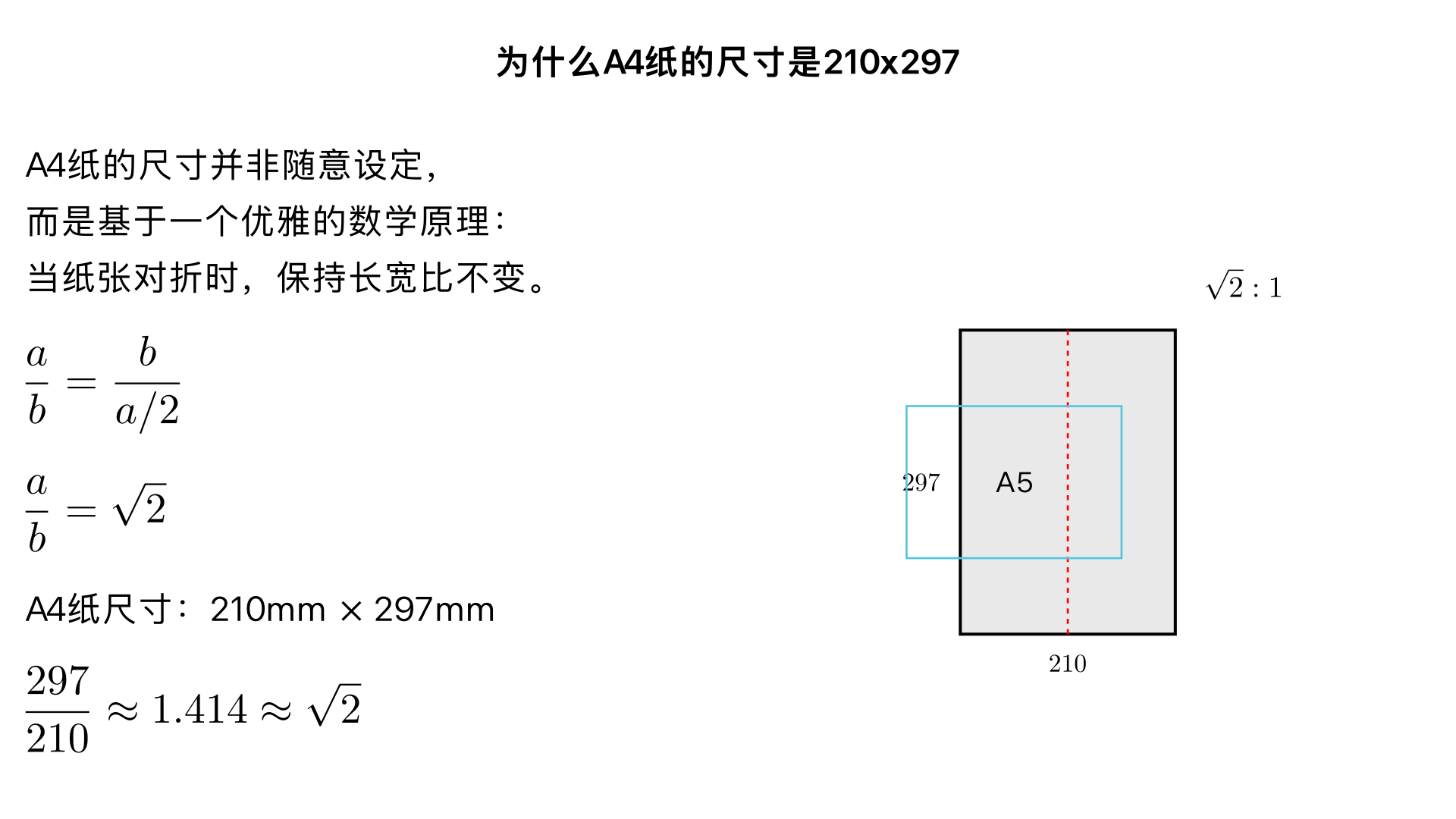
为什么A4纸的尺寸是210x297
▶
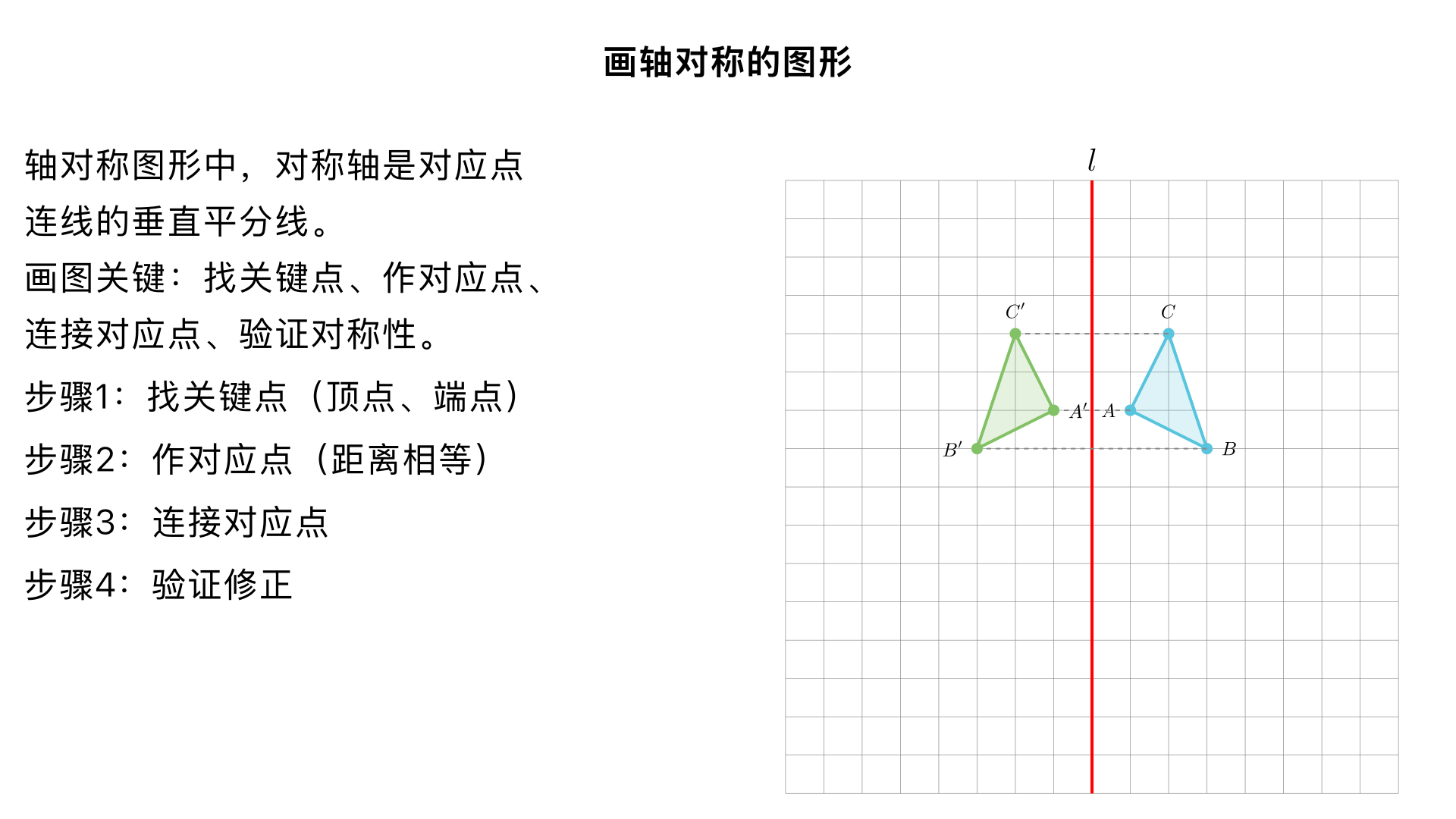
八年级数学 / 轴对称 / 画轴对称的图形 一、核心知识点(5 分钟掌握) 画图依据:轴对称图形中,对称轴是对应点连线的垂直平分线(对应点到对称轴的距离相等,连线与对称轴垂直)。 关键概念: 关键点:图形的顶点、端点、交点(如三角形的 3 个顶点、线段的端点)。 对应点:原图形上的点关于对称轴的对称点。 二、规范画法步骤(以平面图形为例,8 分钟实操) 1. 准备工具 直尺(画直线、量距离)、圆规(画垂直平分线、量等距)、铅笔、纸。 2. 四步画法 步骤 操作细节 ① 找关键点 在原图形上标出所有关键点(如四边形标 4 个顶点,记为 A、B、C、D)。 ② 作对应点 以每个关键点为对象,作关于对称轴 l 的对称点: 1. 过点 A 作直线 l 的垂线(用圆规画弧,交 l 于两点,再作垂直平分线); 2. 在垂线上量取与 A 到 l 相等的距离,得到对称点 A'(确保 A 到 l 的距离 = A' 到 l 的距离); 3. 重复上述操作,得到 B'、C'、D'。 ③ 连对应点 用直尺依次连接 A'、B'、C'、D'(按原图形的顶点顺序连接,避免错乱)。 ④ 验证修正 检查:对应点连线是否垂直于对称轴,对应边长度是否相等,确保图形对称。 3. 网格图简化画法(无圆规时,3 分钟快速画) 若图形在方格纸中,关键点坐标可直接推导: 对称轴为竖直方向(如 x=2):对应点横坐标 = 2×2 - 原横坐标,纵坐标不变(例:A (1,3)→A'(3,3)); 对称轴为水平方向(如 y=1):对应点纵坐标 = 2×1 - 原纵坐标,横坐标不变(例:B (4,2)→B'(4,0))。 三、易错点警示(3 分钟规避) 漏找关键点:忽略线段端点或图形交点,导致对称图形残缺; 距离不等:作对应点时,未量准与对称轴的距离,导致图形不对称; 连线错乱:连接对应点时顺序与原图形不一致,形成 “扭曲图形”; 垂线不垂直:未用圆规规范作垂线,仅凭目测画,导致对应点偏差。 四、典型例题(5 分钟练习 + 解析) 例题:在方格纸中,画出△ABC 关于直线 l 的对称图形(如图,A (1,2)、B (3,1)、C (2,4),对称轴 l 为直线 x=4)。 解析步骤: 确定关键点:A、B、C 三点; 求对应点坐标: A'(2×4 -1, 2)=(7,2); B'(2×4 -3, 1)=(5,1); C'(2×4 -2, 4)=(6,4); 连接 A'、B'、C',得到对称△A'B'C'。 五、即时练习(10 分钟巩固) 基础题:画出边长为 3cm 的正方形关于其竖直中线的对称图形(用圆规 + 直尺规范画); 提升题:在方格纸中,画出梯形 ABCD(A (0,0)、B (4,0)、C (3,2)、D (1,2))关于直线 y=3 的对称图形,写出对应点坐标。
▶
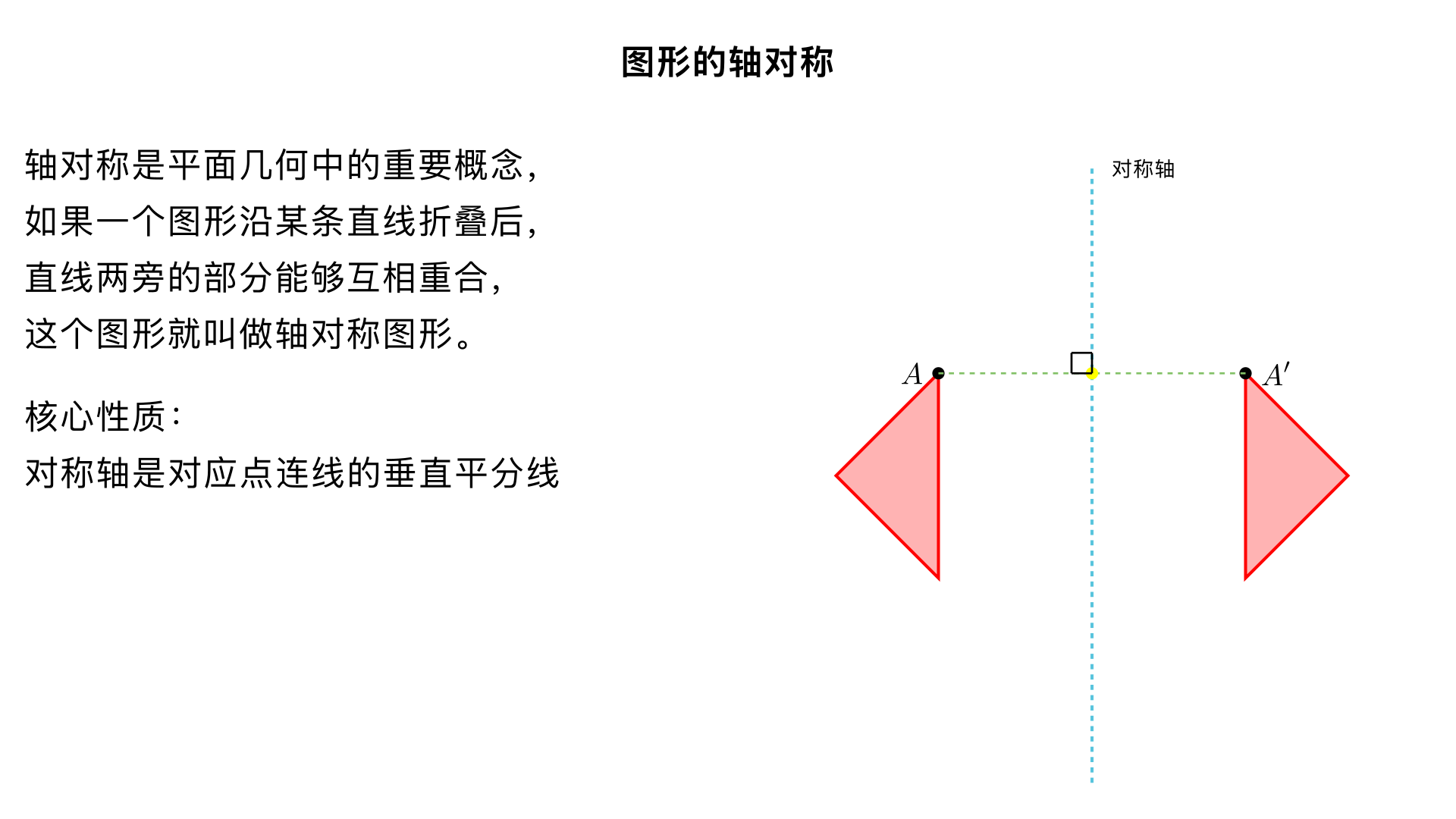
八年级数学 / 轴对称 / 图形的轴对称 一、核心概念(关键定义) 1. 轴对称图形 定义:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是一个图形的自身对称关系 对称轴是直线,不是线段或射线 一个轴对称图形的对称轴可能有一条或多条 2. 两个图形成轴对称 定义:把一个平面图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是两个图形之间的对称关系 这两个图形是全等图形 对应点所连线段被对称轴垂直平分 3. 两者区别与联系 项目 轴对称图形 两个图形成轴对称 图形个数 1 个 2 个 对称关系 自身对称 两个图形之间对称 对称轴 1 条或多条 1 条 联系 都沿直线折叠后重合;对称轴都是对应点连线的垂直平分线;把成轴对称的两个图形看成一个整体,就是轴对称图形 二、轴对称的性质(核心定理) 全等性:成轴对称的两个图形是全等图形,对应边相等,对应角相等。 垂直平分线性质:对称轴是任何一对对应点所连线段的垂直平分线(核心性质)。 对应关系: 对应线段相等,对应线段所在直线的交点在对称轴上(或平行于对称轴) 对应角相等,对应角的两边关于对称轴对称 对称性:轴对称变换不改变图形的形状和大小,只改变图形的位置。 三、常见轴对称图形及对称轴数量 图形 对称轴数量 对称轴描述 线段 2 条 线段的垂直平分线;线段所在的直线 角 1 条 角平分线所在的直线 等腰三角形 1 条 顶角平分线(底边上的高、底边上的中线)所在直线 等边三角形 3 条 每条边上的高(中线、所对角的平分线)所在直线 矩形 2 条 对边中点连线所在直线 菱形 2 条 对角线所在直线 正方形 4 条 对边中点连线 + 两条对角线所在直线 圆 无数条 过圆心的任意直线 正 n 边形 n 条 每条边的垂直平分线(或每个内角的平分线)所在直线 四、对称轴的画法(操作步骤) 找对称点:在图形上选取若干个关键点(顶点、端点等) 作垂线:过每个关键点作对称轴的垂线 量距离:在垂线上截取与该点到对称轴距离相等的线段 连对称点:依次连接所有对称点,得到对称图形 五、轴对称的判定(识别方法) 定义法:沿某条直线折叠后,直线两旁部分完全重合 性质法: 若两个图形的对应点连线都被同一条直线垂直平分,则这两个图形成轴对称 若一个图形的所有点关于某条直线的对称点都在该图形上,则该图形是轴对称图形 六、典型例题与应用 例题 1:基础识别 下列图形中,是轴对称图形的有( )① 等腰三角形 ② 平行四边形 ③ 矩形 ④ 梯形 ⑤ 圆答案:①③⑤(解析:平行四边形无对称轴,一般梯形无对称轴) 例题 2:性质应用 已知△ABC 与△A'B'C' 关于直线 l 对称,AB=5cm,∠A=60°,则 A'B'=,∠A'=答案:5cm,60°(解析:成轴对称的图形对应边相等,对应角相等) 例题 3:作图题 已知线段 AB 和直线 l,画出线段 AB 关于直线 l 的对称线段 A'B'步骤: 过 A 作 l 的垂线,垂足为 O,延长 AO 到 A',使 OA'=OA 过 B 作 l 的垂线,垂足为 P,延长 BP 到 B',使 PB'=PB 连接 A'B',即为所求对称线段 七、易错点与注意事项 对称轴类型:对称轴是直线,不是线段或射线(如角的对称轴是角平分线所在直线,不是角平分线本身) 线段对称轴:线段有两条对称轴,不要漏掉线段所在直线 等腰三角形:对称轴是顶角平分线所在直线,也是底边上的高和中线所在直线(三线合一) 区分概念:不要混淆 “轴对称图形” 和 “两个图形成轴对称” 的概念 八、知识拓展 轴对称变换:由一个图形得到它的轴对称图形的过程叫做轴对称变换,属于全等变换 最短路径问题:利用轴对称性质解决(如 “将军饮马” 问题) 对称美:轴对称图形在建筑、艺术、设计等领域有广泛应用(如故宫、天坛等建筑) 核心口诀:轴对称,很重要,折叠重合是关键。一个图形叫对称,两个图形成轴对称。对称轴是垂直平分线,对应边等角不变。
▶
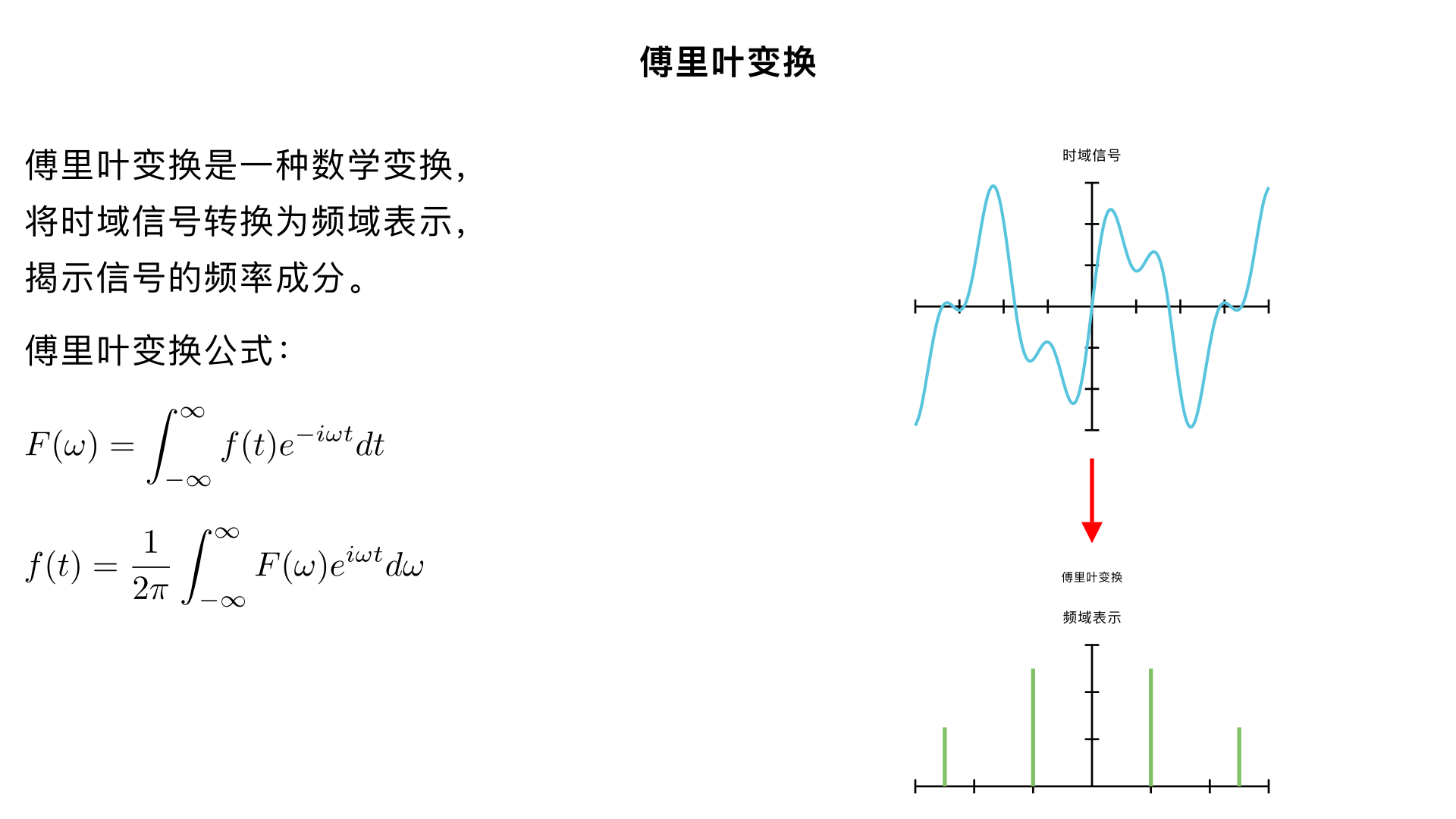
请描述傅里叶变换
▶
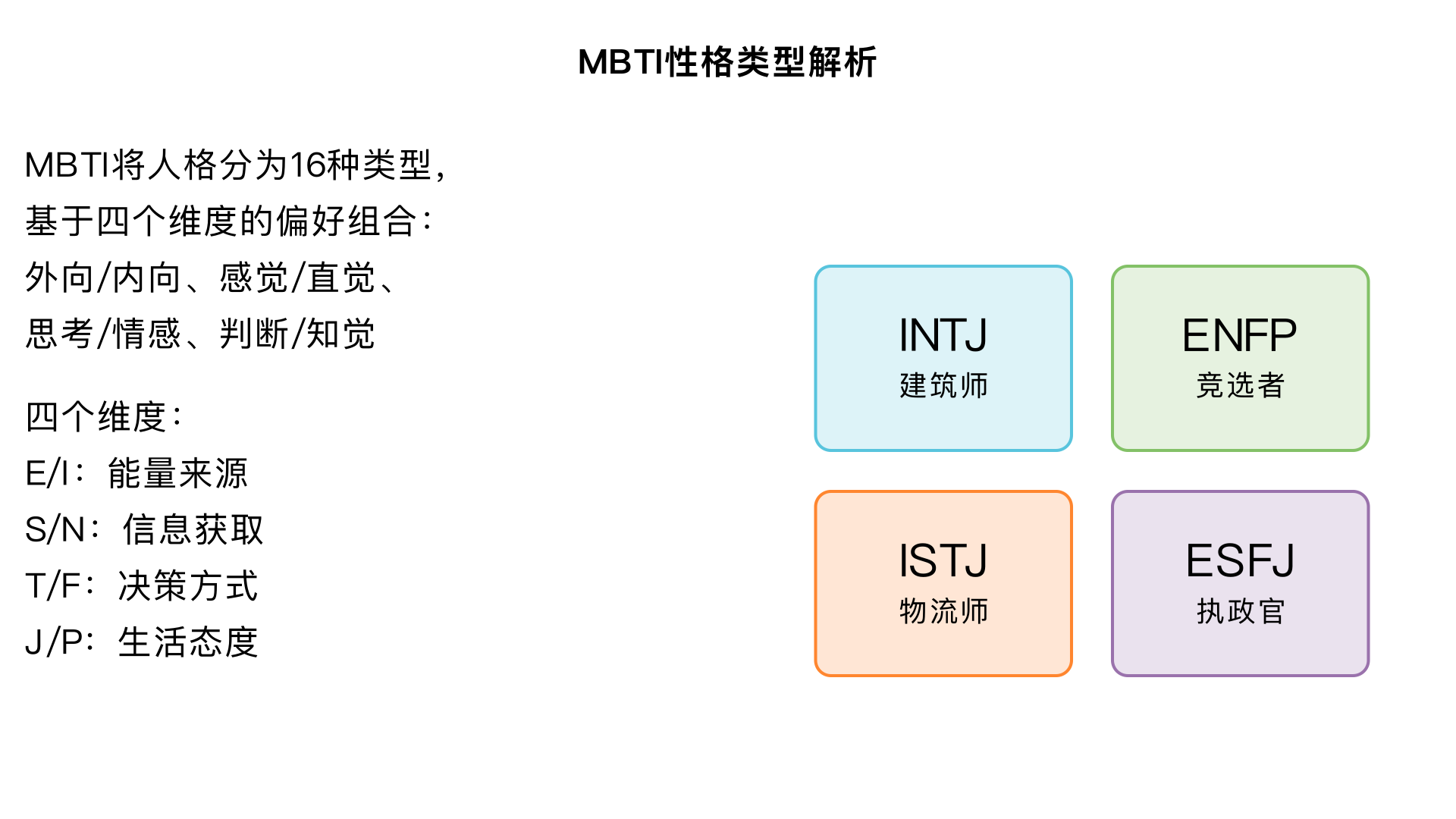
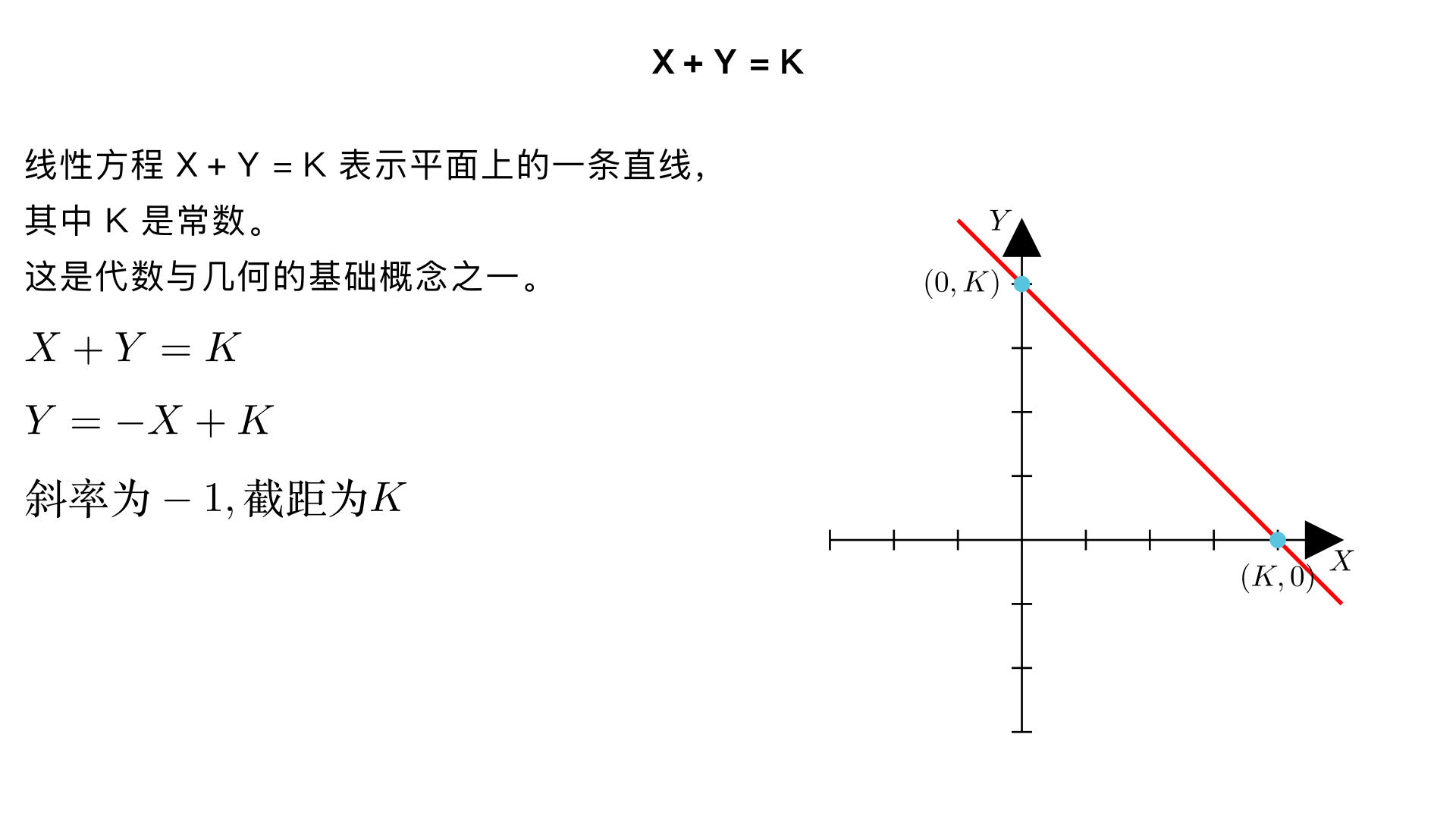
mbti各种性格解释
▶