T
Teach Me AnythingTMA
Video History
Page 11 / 44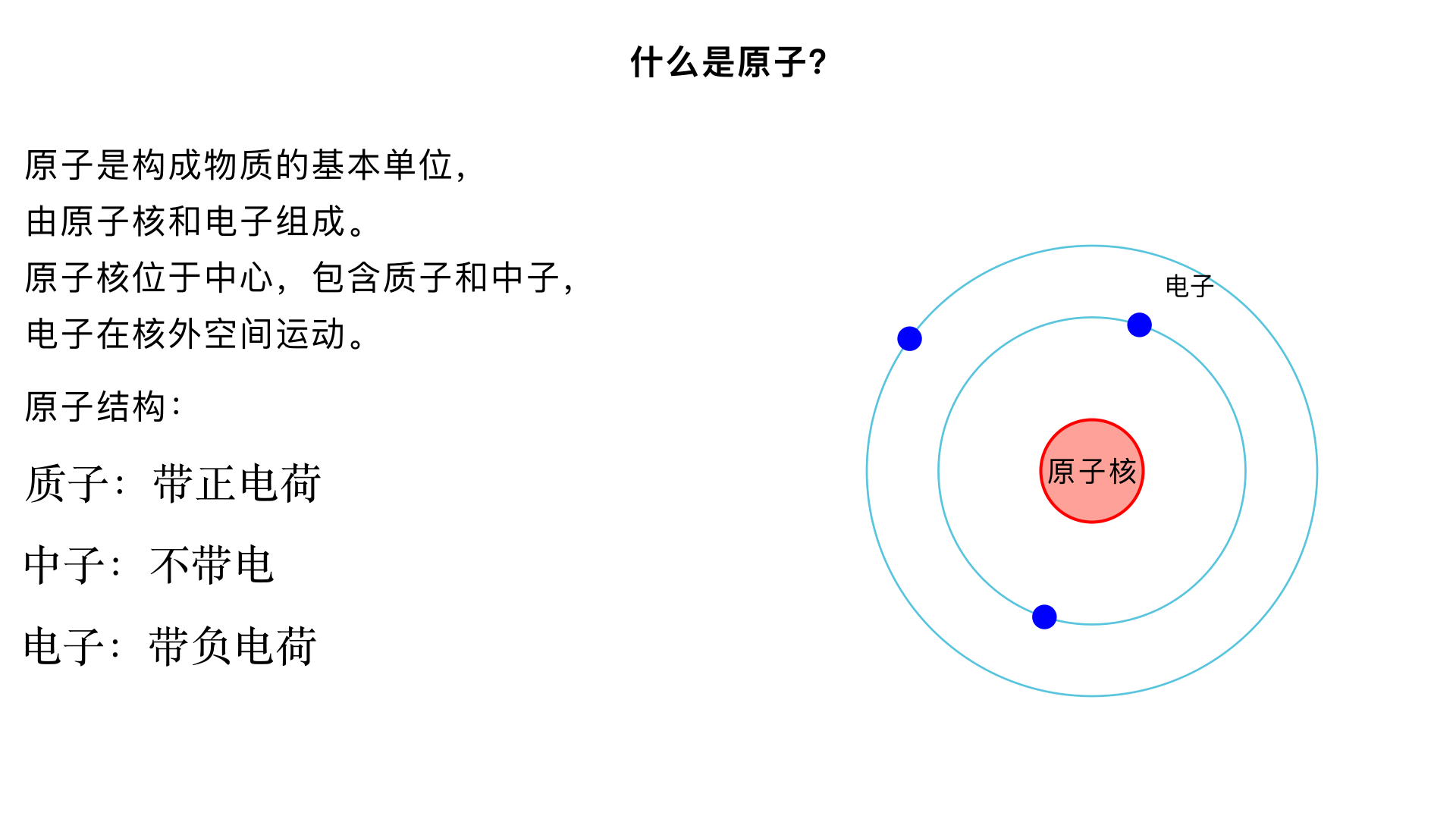
▶
什么是原子?
▶
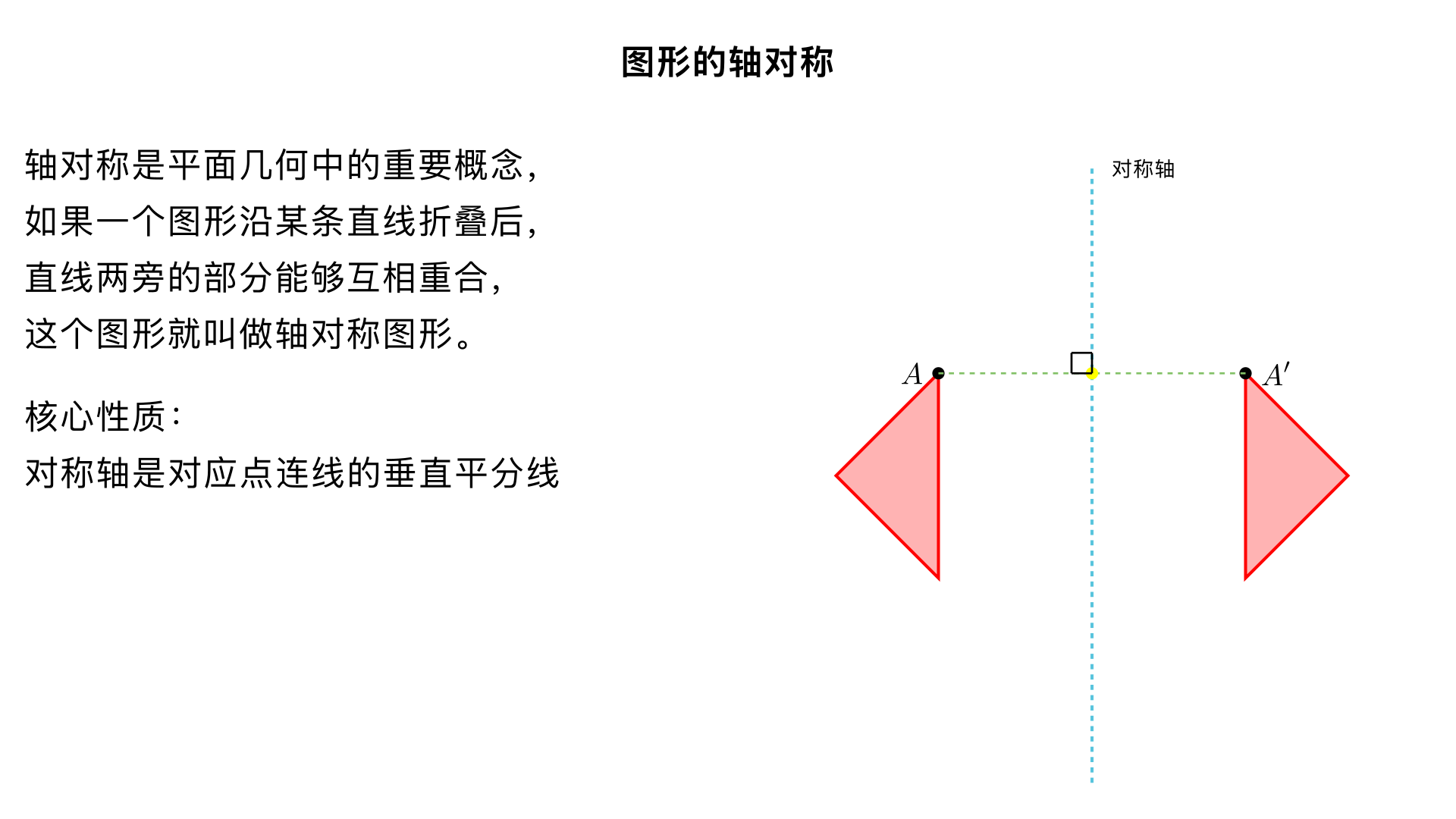
八年级数学 / 轴对称 / 图形的轴对称 一、核心概念(关键定义) 1. 轴对称图形 定义:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是一个图形的自身对称关系 对称轴是直线,不是线段或射线 一个轴对称图形的对称轴可能有一条或多条 2. 两个图形成轴对称 定义:把一个平面图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点是对称点(对应点)。 要点: 研究对象是两个图形之间的对称关系 这两个图形是全等图形 对应点所连线段被对称轴垂直平分 3. 两者区别与联系 项目 轴对称图形 两个图形成轴对称 图形个数 1 个 2 个 对称关系 自身对称 两个图形之间对称 对称轴 1 条或多条 1 条 联系 都沿直线折叠后重合;对称轴都是对应点连线的垂直平分线;把成轴对称的两个图形看成一个整体,就是轴对称图形 二、轴对称的性质(核心定理) 全等性:成轴对称的两个图形是全等图形,对应边相等,对应角相等。 垂直平分线性质:对称轴是任何一对对应点所连线段的垂直平分线(核心性质)。 对应关系: 对应线段相等,对应线段所在直线的交点在对称轴上(或平行于对称轴) 对应角相等,对应角的两边关于对称轴对称 对称性:轴对称变换不改变图形的形状和大小,只改变图形的位置。 三、常见轴对称图形及对称轴数量 图形 对称轴数量 对称轴描述 线段 2 条 线段的垂直平分线;线段所在的直线 角 1 条 角平分线所在的直线 等腰三角形 1 条 顶角平分线(底边上的高、底边上的中线)所在直线 等边三角形 3 条 每条边上的高(中线、所对角的平分线)所在直线 矩形 2 条 对边中点连线所在直线 菱形 2 条 对角线所在直线 正方形 4 条 对边中点连线 + 两条对角线所在直线 圆 无数条 过圆心的任意直线 正 n 边形 n 条 每条边的垂直平分线(或每个内角的平分线)所在直线 四、对称轴的画法(操作步骤) 找对称点:在图形上选取若干个关键点(顶点、端点等) 作垂线:过每个关键点作对称轴的垂线 量距离:在垂线上截取与该点到对称轴距离相等的线段 连对称点:依次连接所有对称点,得到对称图形 五、轴对称的判定(识别方法) 定义法:沿某条直线折叠后,直线两旁部分完全重合 性质法: 若两个图形的对应点连线都被同一条直线垂直平分,则这两个图形成轴对称 若一个图形的所有点关于某条直线的对称点都在该图形上,则该图形是轴对称图形 六、典型例题与应用 例题 1:基础识别 下列图形中,是轴对称图形的有( )① 等腰三角形 ② 平行四边形 ③ 矩形 ④ 梯形 ⑤ 圆答案:①③⑤(解析:平行四边形无对称轴,一般梯形无对称轴) 例题 2:性质应用 已知△ABC 与△A'B'C' 关于直线 l 对称,AB=5cm,∠A=60°,则 A'B'=,∠A'=答案:5cm,60°(解析:成轴对称的图形对应边相等,对应角相等) 例题 3:作图题 已知线段 AB 和直线 l,画出线段 AB 关于直线 l 的对称线段 A'B'步骤: 过 A 作 l 的垂线,垂足为 O,延长 AO 到 A',使 OA'=OA 过 B 作 l 的垂线,垂足为 P,延长 BP 到 B',使 PB'=PB 连接 A'B',即为所求对称线段 七、易错点与注意事项 对称轴类型:对称轴是直线,不是线段或射线(如角的对称轴是角平分线所在直线,不是角平分线本身) 线段对称轴:线段有两条对称轴,不要漏掉线段所在直线 等腰三角形:对称轴是顶角平分线所在直线,也是底边上的高和中线所在直线(三线合一) 区分概念:不要混淆 “轴对称图形” 和 “两个图形成轴对称” 的概念 八、知识拓展 轴对称变换:由一个图形得到它的轴对称图形的过程叫做轴对称变换,属于全等变换 最短路径问题:利用轴对称性质解决(如 “将军饮马” 问题) 对称美:轴对称图形在建筑、艺术、设计等领域有广泛应用(如故宫、天坛等建筑) 核心口诀:轴对称,很重要,折叠重合是关键。一个图形叫对称,两个图形成轴对称。对称轴是垂直平分线,对应边等角不变。
▶
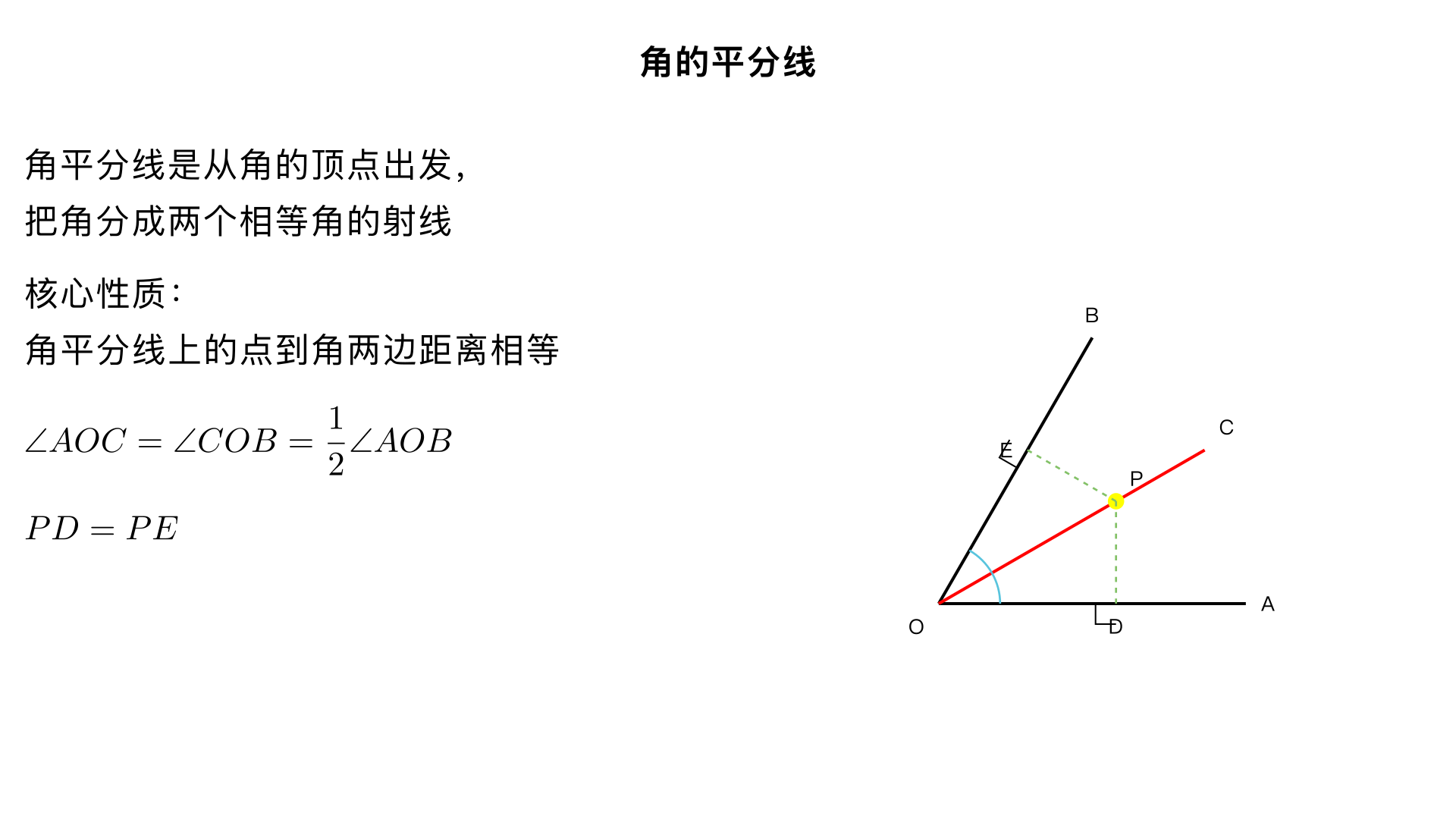
八年级数学 / 全等三角形 / 角的平分线 一、角平分线的定义与尺规作图 1. 定义 从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。 几何表示:若 OC 是∠AOB 的平分线,则∠AOC = ∠COB = ½∠AOB 2. 尺规作图(核心技能) 已知:∠AOB求作:∠AOB 的平分线作法: 以点 O 为圆心,适当长为半径画弧,交 OA 于 M,交 OB 于 N 分别以 M、N 为圆心,大于 ½MN的长为半径画弧,两弧在∠AOB 内部交于点 P 画射线 OP,OP 即为∠AOB 的平分线 原理:SSS 全等判定(△OMP ≌ △ONP),对应角相等,故 OP 平分∠AOB 二、角平分线的核心定理(性质 + 判定) 1. 性质定理(重点) 角平分线上的点到角两边的距离相等 条件 结论 几何表示 ① 点 P 在∠AOB 的平分线上 ② PD⊥OA,PE⊥OB PD = PE ∵ OP 平分∠AOB PD⊥OA,PE⊥OB ∴ PD = PE 证明:用 AAS 判定△OPD ≌ △OPE,对应边 PD = PE 2. 判定定理(性质的逆定理) 角的内部到角两边距离相等的点,在这个角的平分线上 条件 结论 几何表示 ① 点 P 在∠AOB 内部 ② PD⊥OA,PE⊥OB ③ PD = PE 点 P 在∠AOB 的平分线上 ∵ PD⊥OA,PE⊥OB,PD = PE ∴ 点 P 在∠AOB 的平分线上 证明:用 HL 判定 Rt△OPD ≌ Rt△OPE,对应角∠AOP = ∠BOP 3. 重要推论 角的平分线是到角两边距离相等的所有点的集合 三、三角形的角平分线 1. 定义 三角形一个内角的平分线与对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线 2. 核心性质(必记) 三角形的三条角平分线相交于一点,这一点叫做三角形的内心 内心到三角形三边的距离相等(内心性质) 内心一定在三角形内部 证明:利用角平分线判定定理,证明三条角平分线交于同一点,该点到三边距离相等 四、角平分线常用辅助线(解题关键) 辅助线类型 作法 适用场景 原理 向两边作垂线 过角平分线上一点作两边的垂线段 证明线段相等、角相等 角平分线性质,构造全等直角三角形(AAS/HL) 截取构全等 在角两边截取相等线段,连接角平分线上点 证明线段和差、角相等 SAS 全等判定,构造对称全等三角形 作角平分线的垂线 延长垂线与角另一边相交 证明线段相等、构造等腰三角形 等腰三角形三线合一,构造对称图形 角平分线 + 平行线 过角一边上点作角平分线的平行线 构造等腰三角形 等角对等边,平行线性质 口诀:图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看 五、典型例题与解法(全等三角形应用) 例 1:性质定理应用 已知:在△ABC 中,∠C = 90°,AD 平分∠BAC,DE⊥AB 于 E,AC = 6,BC = 8求:CD 的长 解法: ∵ AD 平分∠BAC,DC⊥AC,DE⊥AB ∴ CD = DE(角平分线性质) 设 CD = x,则 DE = x,DB = 8 - x 易证 Rt△ACD ≌ Rt△AED(HL),故 AE = AC = 6 AB = √(AC² + BC²) = 10,BE = AB - AE = 4 在 Rt△BDE 中,x² + 4² = (8 - x)²,解得 x = 3 答案:CD = 3 例 2:判定定理应用 已知:在四边形 ABCD 中,∠B = ∠D = 90°,点 E 在 BC 上,且 AE 平分∠BAD,CE = DE求证:BE = DE 证明: 过 E 作 EF⊥AD 于 F ∵ AE 平分∠BAD,∠B = 90°,EF⊥AD ∴ BE = EF(角平分线性质) ∵ ∠D = 90°,CE = DE,且 CE⊥CD,DE⊥CD ∴ 点 E 在∠ADC 的平分线上(角平分线判定) 又 EF⊥AD,DE⊥CD,故 EF = DE ∴ BE = DE(等量代换) 例 3:辅助线构造(截取法) 已知:AD 平分∠BAC,AB > AC,求证:AB - AC = BD - DC 证明: 在 AB 上截取 AE = AC(构造全等) ∵ AD 平分∠BAC,故∠EAD = ∠CAD 在△AED 和△ACD 中: AE = AC,∠EAD = ∠CAD,AD = AD ∴ △AED ≌ △ACD(SAS),故 DE = DC AB - AC = AB - AE = BE BD - DC = BD - DE 在△BDE 中,BE = BD - DE(线段和差) ∴ AB - AC = BD - DC 六、易错点与注意事项 性质定理的两个必要条件: 点在角平分线上 到角两边的距离(必须是垂线段) 易错:忽略垂直关系,直接说 "角平分线上的点到角两边的线段相等" 判定定理的前提: 点必须在角的内部(外部点不适用) 三角形角平分线与角平分线区别: 前者是线段,后者是射线 内心与外心区别: 内心:三条角平分线交点,到三边距离相等 外心:三边垂直平分线交点,到三个顶点距离相等 七、思维导图(核心知识框架) plaintext 角的平分线 ├── 定义:分角为两等份的射线 ├── 尺规作图:三步骤+SSS原理 ├── 两大定理 │ ├── 性质:角平分线上点→到两边距离相等 │ └── 判定:到两边距离相等点→在角平分线上 ├── 三角形角平分线 │ ├── 定义:内角平分线与对边交点的线段 │ └── 性质:三线共点(内心),到三边等距 └── 辅助线技巧 ├── 向两边作垂线 ├── 截取构全等 ├── 作角平分线垂线 └── 角平分线+平行线 八、巩固练习(基础 + 提升) 基础题 如图,OP 平分∠AOB,PC⊥OA 于 C,PD⊥OB 于 D,PC = 3,则 PD = ____(答案:3) 三角形的三条角平分线相交于一点,这个点叫做三角形的____(答案:内心) 提升题 已知:在△ABC 中,∠B = 60°,∠C = 40°,AD 平分∠BAC,求∠ADC 的度数(答案:100°) 如图,∠B = ∠C = 90°,M 是 BC 中点,DM 平分∠ADC,求证:AM 平分∠DAB(提示:作 MN⊥AD 于 N)
▶
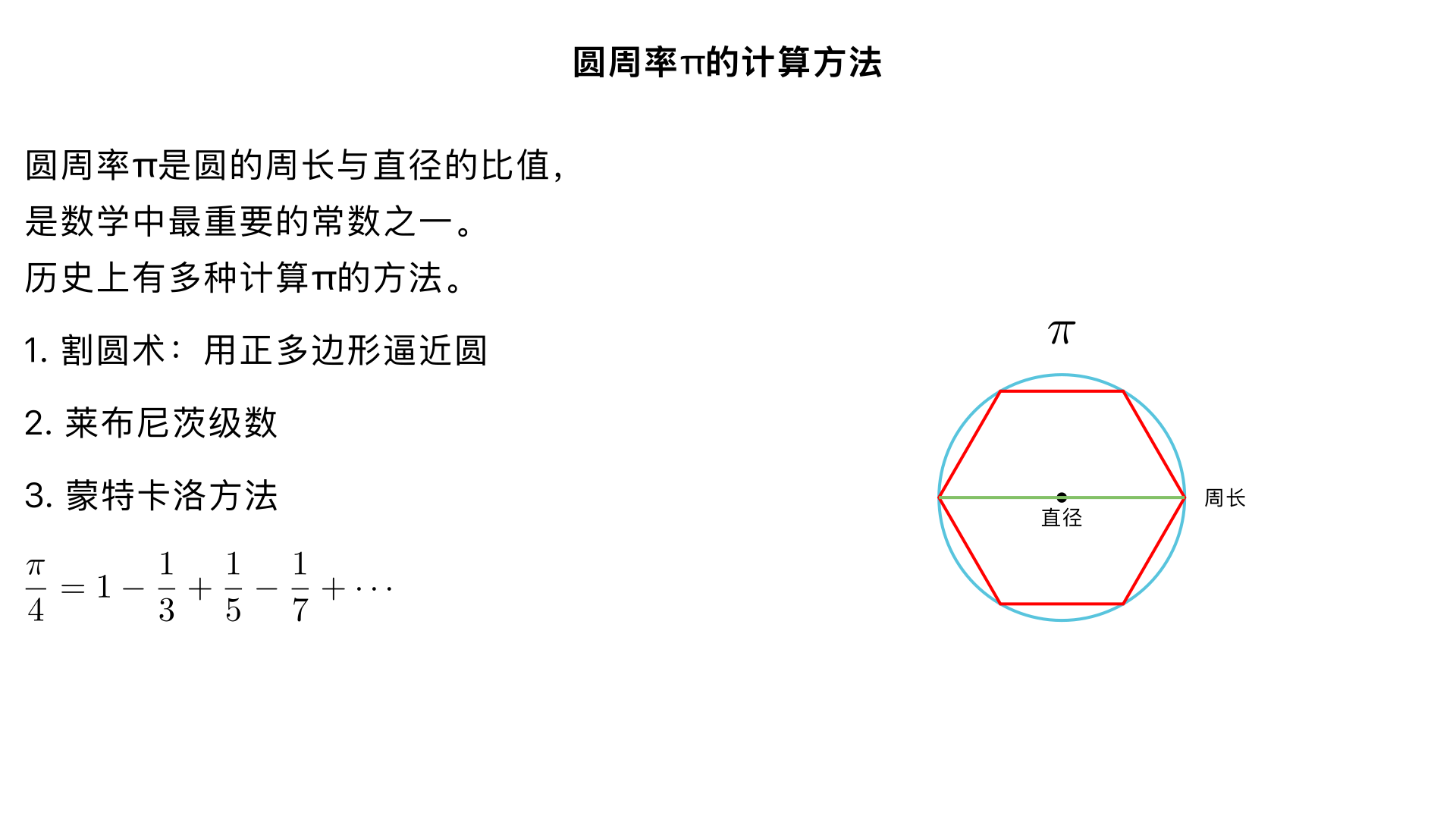
描述一下π是怎么计算出来的
▶
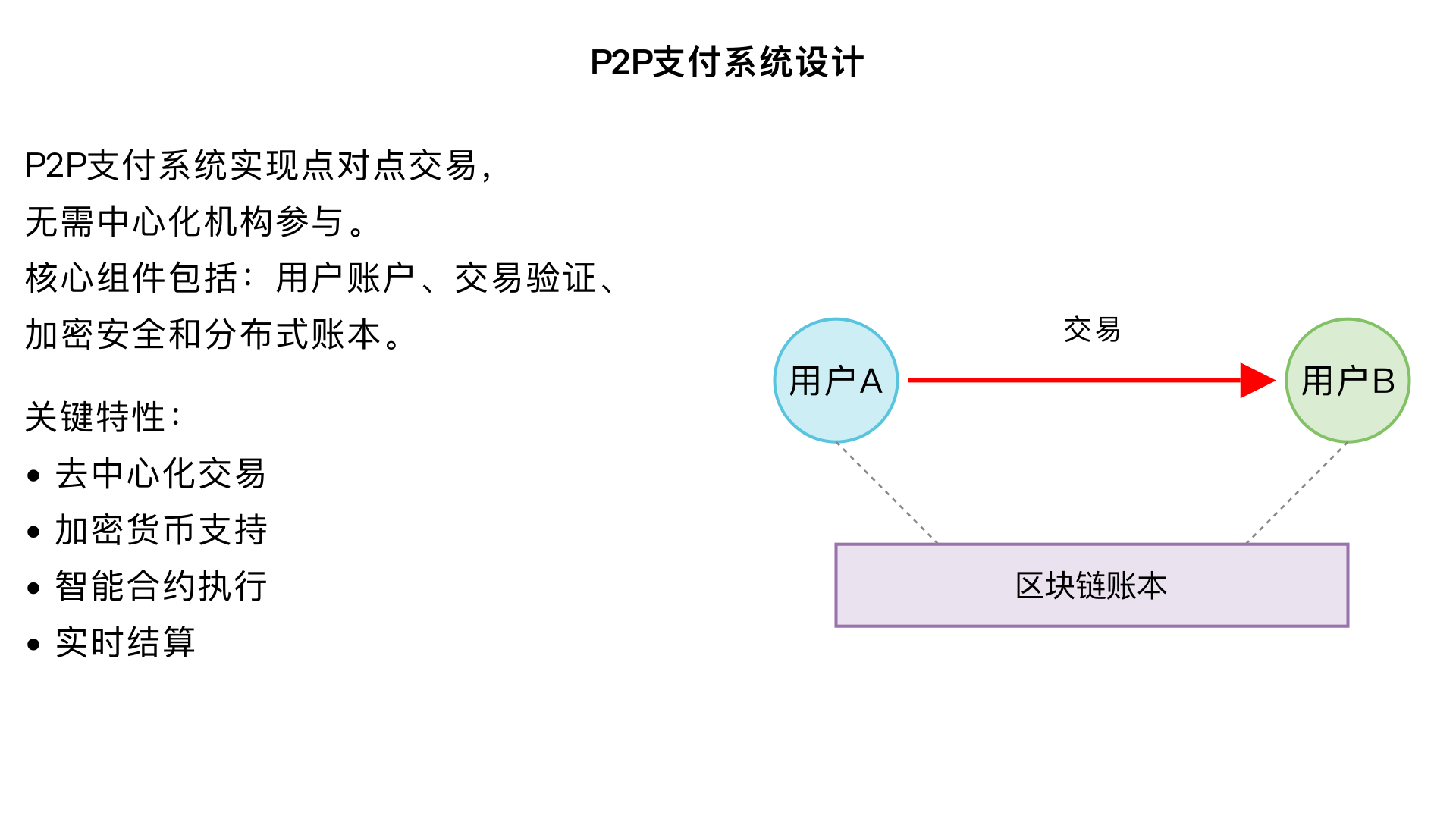
怎么生成一个payment系统,p2p transaction相关的

▶
八年级数学 / 全等三角形 / 角的平分线 一、角平分线的定义与尺规作图 1. 定义 从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。 几何表示:若 OC 是∠AOB 的平分线,则∠AOC = ∠COB = ½∠AOB 2. 尺规作图(核心技能) 已知:∠AOB求作:∠AOB 的平分线作法: 以点 O 为圆心,适当长为半径画弧,交 OA 于 M,交 OB 于 N 分别以 M、N 为圆心,大于 ½MN的长为半径画弧,两弧在∠AOB 内部交于点 P 画射线 OP,OP 即为∠AOB 的平分线 原理:SSS 全等判定(△OMP ≌ △ONP),对应角相等,故 OP 平分∠AOB 二、角平分线的核心定理(性质 + 判定) 1. 性质定理(重点) 角平分线上的点到角两边的距离相等 条件 结论 几何表示 ① 点 P 在∠AOB 的平分线上 ② PD⊥OA,PE⊥OB PD = PE ∵ OP 平分∠AOB PD⊥OA,PE⊥OB ∴ PD = PE 证明:用 AAS 判定△OPD ≌ △OPE,对应边 PD = PE 2. 判定定理(性质的逆定理) 角的内部到角两边距离相等的点,在这个角的平分线上 条件 结论 几何表示 ① 点 P 在∠AOB 内部 ② PD⊥OA,PE⊥OB ③ PD = PE 点 P 在∠AOB 的平分线上 ∵ PD⊥OA,PE⊥OB,PD = PE ∴ 点 P 在∠AOB 的平分线上 证明:用 HL 判定 Rt△OPD ≌ Rt△OPE,对应角∠AOP = ∠BOP 3. 重要推论 角的平分线是到角两边距离相等的所有点的集合 三、三角形的角平分线 1. 定义 三角形一个内角的平分线与对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线 2. 核心性质(必记) 三角形的三条角平分线相交于一点,这一点叫做三角形的内心 内心到三角形三边的距离相等(内心性质) 内心一定在三角形内部 证明:利用角平分线判定定理,证明三条角平分线交于同一点,该点到三边距离相等 四、角平分线常用辅助线(解题关键) 辅助线类型 作法 适用场景 原理 向两边作垂线 过角平分线上一点作两边的垂线段 证明线段相等、角相等 角平分线性质,构造全等直角三角形(AAS/HL) 截取构全等 在角两边截取相等线段,连接角平分线上点 证明线段和差、角相等 SAS 全等判定,构造对称全等三角形 作角平分线的垂线 延长垂线与角另一边相交 证明线段相等、构造等腰三角形 等腰三角形三线合一,构造对称图形 角平分线 + 平行线 过角一边上点作角平分线的平行线 构造等腰三角形 等角对等边,平行线性质 口诀:图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看 五、典型例题与解法(全等三角形应用) 例 1:性质定理应用 已知:在△ABC 中,∠C = 90°,AD 平分∠BAC,DE⊥AB 于 E,AC = 6,BC = 8求:CD 的长 解法: ∵ AD 平分∠BAC,DC⊥AC,DE⊥AB ∴ CD = DE(角平分线性质) 设 CD = x,则 DE = x,DB = 8 - x 易证 Rt△ACD ≌ Rt△AED(HL),故 AE = AC = 6 AB = √(AC² + BC²) = 10,BE = AB - AE = 4 在 Rt△BDE 中,x² + 4² = (8 - x)²,解得 x = 3 答案:CD = 3 例 2:判定定理应用 已知:在四边形 ABCD 中,∠B = ∠D = 90°,点 E 在 BC 上,且 AE 平分∠BAD,CE = DE求证:BE = DE 证明: 过 E 作 EF⊥AD 于 F ∵ AE 平分∠BAD,∠B = 90°,EF⊥AD ∴ BE = EF(角平分线性质) ∵ ∠D = 90°,CE = DE,且 CE⊥CD,DE⊥CD ∴ 点 E 在∠ADC 的平分线上(角平分线判定) 又 EF⊥AD,DE⊥CD,故 EF = DE ∴ BE = DE(等量代换) 例 3:辅助线构造(截取法) 已知:AD 平分∠BAC,AB > AC,求证:AB - AC = BD - DC 证明: 在 AB 上截取 AE = AC(构造全等) ∵ AD 平分∠BAC,故∠EAD = ∠CAD 在△AED 和△ACD 中: AE = AC,∠EAD = ∠CAD,AD = AD ∴ △AED ≌ △ACD(SAS),故 DE = DC AB - AC = AB - AE = BE BD - DC = BD - DE 在△BDE 中,BE = BD - DE(线段和差) ∴ AB - AC = BD - DC 六、易错点与注意事项 性质定理的两个必要条件: 点在角平分线上 到角两边的距离(必须是垂线段) 易错:忽略垂直关系,直接说 "角平分线上的点到角两边的线段相等" 判定定理的前提: 点必须在角的内部(外部点不适用) 三角形角平分线与角平分线区别: 前者是线段,后者是射线 内心与外心区别: 内心:三条角平分线交点,到三边距离相等 外心:三边垂直平分线交点,到三个顶点距离相等 七、思维导图(核心知识框架) plaintext 角的平分线 ├── 定义:分角为两等份的射线 ├── 尺规作图:三步骤+SSS原理 ├── 两大定理 │ ├── 性质:角平分线上点→到两边距离相等 │ └── 判定:到两边距离相等点→在角平分线上 ├── 三角形角平分线 │ ├── 定义:内角平分线与对边交点的线段 │ └── 性质:三线共点(内心),到三边等距 └── 辅助线技巧 ├── 向两边作垂线 ├── 截取构全等 ├── 作角平分线垂线 └── 角平分线+平行线 八、巩固练习(基础 + 提升) 基础题 如图,OP 平分∠AOB,PC⊥OA 于 C,PD⊥OB 于 D,PC = 3,则 PD = ____(答案:3) 三角形的三条角平分线相交于一点,这个点叫做三角形的____(答案:内心) 提升题 已知:在△ABC 中,∠B = 60°,∠C = 40°,AD 平分∠BAC,求∠ADC 的度数(答案:100°) 如图,∠B = ∠C = 90°,M 是 BC 中点,DM 平分∠ADC,求证:AM 平分∠DAB(提示:作 MN⊥AD 于 N)

▶
八年级数学 / 全等三角形 / 角的平分线 一、角平分线的定义与尺规作图 1. 定义 从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。 几何表示:若 OC 是∠AOB 的平分线,则∠AOC = ∠COB = ½∠AOB 2. 尺规作图(核心技能) 已知:∠AOB求作:∠AOB 的平分线作法: 以点 O 为圆心,适当长为半径画弧,交 OA 于 M,交 OB 于 N 分别以 M、N 为圆心,大于 ½MN的长为半径画弧,两弧在∠AOB 内部交于点 P 画射线 OP,OP 即为∠AOB 的平分线 原理:SSS 全等判定(△OMP ≌ △ONP),对应角相等,故 OP 平分∠AOB 二、角平分线的核心定理(性质 + 判定) 1. 性质定理(重点) 角平分线上的点到角两边的距离相等 条件 结论 几何表示 ① 点 P 在∠AOB 的平分线上 ② PD⊥OA,PE⊥OB PD = PE ∵ OP 平分∠AOB PD⊥OA,PE⊥OB ∴ PD = PE 证明:用 AAS 判定△OPD ≌ △OPE,对应边 PD = PE 2. 判定定理(性质的逆定理) 角的内部到角两边距离相等的点,在这个角的平分线上 条件 结论 几何表示 ① 点 P 在∠AOB 内部 ② PD⊥OA,PE⊥OB ③ PD = PE 点 P 在∠AOB 的平分线上 ∵ PD⊥OA,PE⊥OB,PD = PE ∴ 点 P 在∠AOB 的平分线上 证明:用 HL 判定 Rt△OPD ≌ Rt△OPE,对应角∠AOP = ∠BOP 3. 重要推论 角的平分线是到角两边距离相等的所有点的集合 三、三角形的角平分线 1. 定义 三角形一个内角的平分线与对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线 2. 核心性质(必记) 三角形的三条角平分线相交于一点,这一点叫做三角形的内心 内心到三角形三边的距离相等(内心性质) 内心一定在三角形内部 证明:利用角平分线判定定理,证明三条角平分线交于同一点,该点到三边距离相等 四、角平分线常用辅助线(解题关键) 辅助线类型 作法 适用场景 原理 向两边作垂线 过角平分线上一点作两边的垂线段 证明线段相等、角相等 角平分线性质,构造全等直角三角形(AAS/HL) 截取构全等 在角两边截取相等线段,连接角平分线上点 证明线段和差、角相等 SAS 全等判定,构造对称全等三角形 作角平分线的垂线 延长垂线与角另一边相交 证明线段相等、构造等腰三角形 等腰三角形三线合一,构造对称图形 角平分线 + 平行线 过角一边上点作角平分线的平行线 构造等腰三角形 等角对等边,平行线性质 口诀:图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看 五、典型例题与解法(全等三角形应用) 例 1:性质定理应用 已知:在△ABC 中,∠C = 90°,AD 平分∠BAC,DE⊥AB 于 E,AC = 6,BC = 8求:CD 的长 解法: ∵ AD 平分∠BAC,DC⊥AC,DE⊥AB ∴ CD = DE(角平分线性质) 设 CD = x,则 DE = x,DB = 8 - x 易证 Rt△ACD ≌ Rt△AED(HL),故 AE = AC = 6 AB = √(AC² + BC²) = 10,BE = AB - AE = 4 在 Rt△BDE 中,x² + 4² = (8 - x)²,解得 x = 3 答案:CD = 3 例 2:判定定理应用 已知:在四边形 ABCD 中,∠B = ∠D = 90°,点 E 在 BC 上,且 AE 平分∠BAD,CE = DE求证:BE = DE 证明: 过 E 作 EF⊥AD 于 F ∵ AE 平分∠BAD,∠B = 90°,EF⊥AD ∴ BE = EF(角平分线性质) ∵ ∠D = 90°,CE = DE,且 CE⊥CD,DE⊥CD ∴ 点 E 在∠ADC 的平分线上(角平分线判定) 又 EF⊥AD,DE⊥CD,故 EF = DE ∴ BE = DE(等量代换) 例 3:辅助线构造(截取法) 已知:AD 平分∠BAC,AB > AC,求证:AB - AC = BD - DC 证明: 在 AB 上截取 AE = AC(构造全等) ∵ AD 平分∠BAC,故∠EAD = ∠CAD 在△AED 和△ACD 中: AE = AC,∠EAD = ∠CAD,AD = AD ∴ △AED ≌ △ACD(SAS),故 DE = DC AB - AC = AB - AE = BE BD - DC = BD - DE 在△BDE 中,BE = BD - DE(线段和差) ∴ AB - AC = BD - DC 六、易错点与注意事项 性质定理的两个必要条件: 点在角平分线上 到角两边的距离(必须是垂线段) 易错:忽略垂直关系,直接说 "角平分线上的点到角两边的线段相等" 判定定理的前提: 点必须在角的内部(外部点不适用) 三角形角平分线与角平分线区别: 前者是线段,后者是射线 内心与外心区别: 内心:三条角平分线交点,到三边距离相等 外心:三边垂直平分线交点,到三个顶点距离相等 七、思维导图(核心知识框架) plaintext 角的平分线 ├── 定义:分角为两等份的射线 ├── 尺规作图:三步骤+SSS原理 ├── 两大定理 │ ├── 性质:角平分线上点→到两边距离相等 │ └── 判定:到两边距离相等点→在角平分线上 ├── 三角形角平分线 │ ├── 定义:内角平分线与对边交点的线段 │ └── 性质:三线共点(内心),到三边等距 └── 辅助线技巧 ├── 向两边作垂线 ├── 截取构全等 ├── 作角平分线垂线 └── 角平分线+平行线 八、巩固练习(基础 + 提升) 基础题 如图,OP 平分∠AOB,PC⊥OA 于 C,PD⊥OB 于 D,PC = 3,则 PD = ____(答案:3) 三角形的三条角平分线相交于一点,这个点叫做三角形的____(答案:内心) 提升题 已知:在△ABC 中,∠B = 60°,∠C = 40°,AD 平分∠BAC,求∠ADC 的度数(答案:100°) 如图,∠B = ∠C = 90°,M 是 BC 中点,DM 平分∠ADC,求证:AM 平分∠DAB(提示:作 MN⊥AD 于 N)
▶
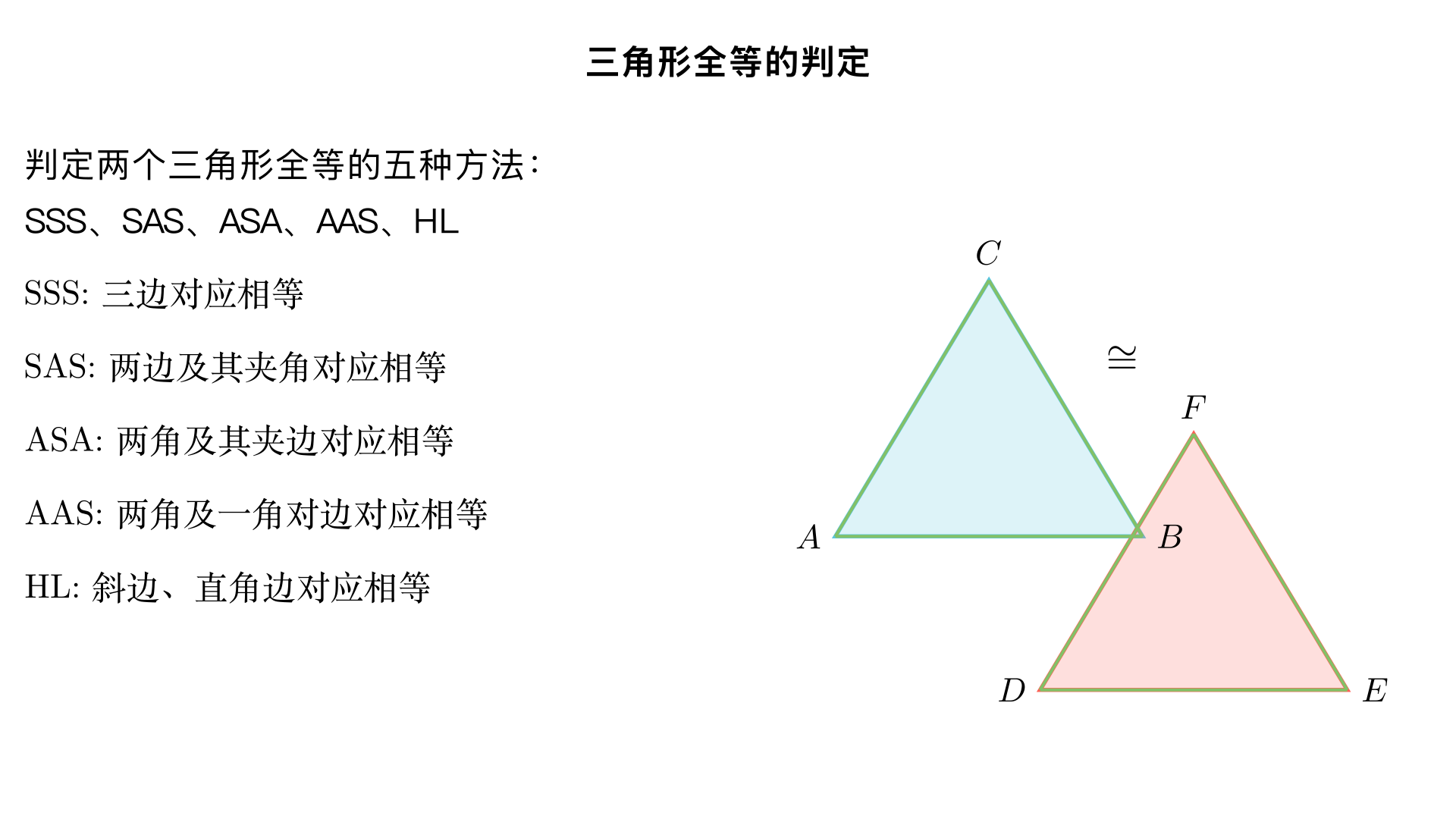
八年级数学 / 全等三角形 / 三角形全等的判定 总览:判定两个三角形全等,无需验证全部 6 组对应元素(三边三角),满足以下5 种标准组合之一即可判定,核心判定方法包括SSS、SAS、ASA、AAS、HL(HL 仅适用于直角三角形)。 一、全等判定核心定理(5 种) 1. 边边边(SSS)— 三边对应相等判定全等 文字表述:如果两个三角形的三条边分别对应相等,那么这两个三角形全等(简记 “边边边” 或 “SSS”)。 符号语言:在△ABC 和△DEF 中, ∵ AB=DE,BC=EF,AC=DF ∴ △ABC ≌ △DEF(SSS) 图形示意:三边固定,三角形形状、大小唯一确定(三角形稳定性)。 适用场景:已知三边长度,或可证三边对应相等(如公共边)。 易错提醒:书写时顶点顺序必须对应,如△ABC≌△DEF,不可写成△ABC≌△DFE。 2. 边角边(SAS)— 两边及其夹角判定全等 文字表述:如果两个三角形的两边及其夹角分别对应相等,那么这两个三角形全等(简记 “边角边” 或 “SAS”)。 符号语言:在△ABC 和△DEF 中, ∵ AB=DE,∠ABC=∠DEF,BC=EF ∴ △ABC ≌ △DEF(SAS) 图形示意:两边夹一角固定,三角形唯一确定。 关键注意:必须是两边的夹角,而非一边的对角(SSA 不可判定全等)。 适用场景:已知两边及夹角,或可证两边及夹角对应相等(如对顶角、公共角)。 3. 角边角(ASA)— 两角及其夹边判定全等 文字表述:如果两个三角形的两角及其夹边分别对应相等,那么这两个三角形全等(简记 “角边角” 或 “ASA”)。 符号语言:在△ABC 和△DEF 中, ∵ ∠ABC=∠DEF,BC=EF,∠ACB=∠DFE ∴ △ABC ≌ △DEF(ASA) 图形示意:两角夹一边固定,三角形唯一确定。 适用场景:已知两角及夹边,或可证两角及夹边对应相等(如平行线、角平分线)。 4. 角角边(AAS)— 两角及一角对边判定全等 文字表述:如果两个三角形的两角及其中一角的对边分别对应相等,那么这两个三角形全等(简记 “角角边” 或 “AAS”)。 符号语言:在△ABC 和△DEF 中, ∵ ∠ABC=∠DEF,∠ACB=∠DFE,AC=DF ∴ △ABC ≌ △DEF(AAS) 逻辑关系:由三角形内角和为 180°,AAS 可由 ASA 推导得出(两角确定则第三角必相等)。 适用场景:已知两角及任意一边,或可证两角及一角对边对应相等。 5. 斜边、直角边(HL)— 直角三角形专属判定 文字表述:斜边和一条直角边分别相等的两个直角三角形全等(简记 “斜边、直角边” 或 “HL”)。 符号语言:在 Rt△ABC 和 Rt△DEF 中(∠C=∠F=90°), ∵ AB=DE(斜边),BC=EF(直角边) ∴ Rt△ABC ≌ Rt△DEF(HL) 适用场景:仅适用于直角三角形,已知斜边和一条直角边,或可证两者对应相等。 二、判定方法对比表(速记) 判定方法 条件组合 适用范围 核心要点 SSS 三边对应相等 所有三角形 三边固定,形状唯一 SAS 两边 + 夹角对应相等 所有三角形 必须是夹角,非对角 ASA 两角 + 夹边对应相等 所有三角形 两角夹边固定,形状唯一 AAS 两角 + 一角对边对应相等 所有三角形 由 ASA 推导,适用更广 HL 斜边 + 直角边对应相等 仅直角三角形 直角三角形专属判定 三、常见误区与关键提醒 SSA 不能判定全等两边及其中一边的对角对应相等,不能保证三角形全等(存在两种不同三角形)。仅当该角为直角(即 HL)或钝角时,才可能判定全等(需额外证明)。 AAA 不能判定全等三角对应相等只能保证相似,不能保证全等(如大小不同的等边三角形)。 书写规范全等符号 “≌” 的顶点顺序必须对应,如△ABC≌△DEF,表示 A↔D、B↔E、C↔F,后续找对应边、对应角需严格按此顺序。 公共元素应用证明时优先寻找公共边、公共角、对顶角等隐含相等条件,简化证明步骤。 四、全等证明基本步骤(四步法) 明确目标:确定要证明全等的两个三角形。 寻找条件:从已知出发,结合图形性质(如角平分线、平行线、垂直等),找对应边、对应角相等的条件。 选择判定:根据找到的条件,匹配 SSS、SAS、ASA、AAS、HL 中的一种。 规范书写: 写清在两个三角形中; 列全三个条件(注明来源,如已知、公共边、已证等); 写出判定依据,得出全等结论; 如需,进一步推导对应边或对应角相等(全等三角形性质)。 五、基础练习(即时巩固) 练习 1(SSS) 如图,AB=AD,BC=DC,求证:△ABC≌△ADC。证明:在△ABC 和△ADC 中,AB=AD(已知),BC=DC(已知),AC=AC(公共边),∴ △ABC≌△ADC(SSS)。 练习 2(SAS) 如图,AB=AC,AD=AE,∠1=∠2,求证:△ABD≌△ACE。证明:∵ ∠1=∠2,∴ ∠1+∠BAC=∠2+∠BAC,即∠BAD=∠CAE。在△ABD 和△ACE 中,AB=AC(已知),∠BAD=∠CAE(已证),AD=AE(已知),∴ △ABD≌△ACE(SAS)。 练习 3(HL) 如图,在 Rt△ABC 和 Rt△DEF 中,∠C=∠F=90°,AB=DE,BC=EF,求证:△ABC≌△DEF。证明:在 Rt△ABC 和 Rt△DEF 中,AB=DE(已知,斜边),BC=EF(已知,直角边),∴ Rt△ABC≌Rt△DEF(HL)。
▶
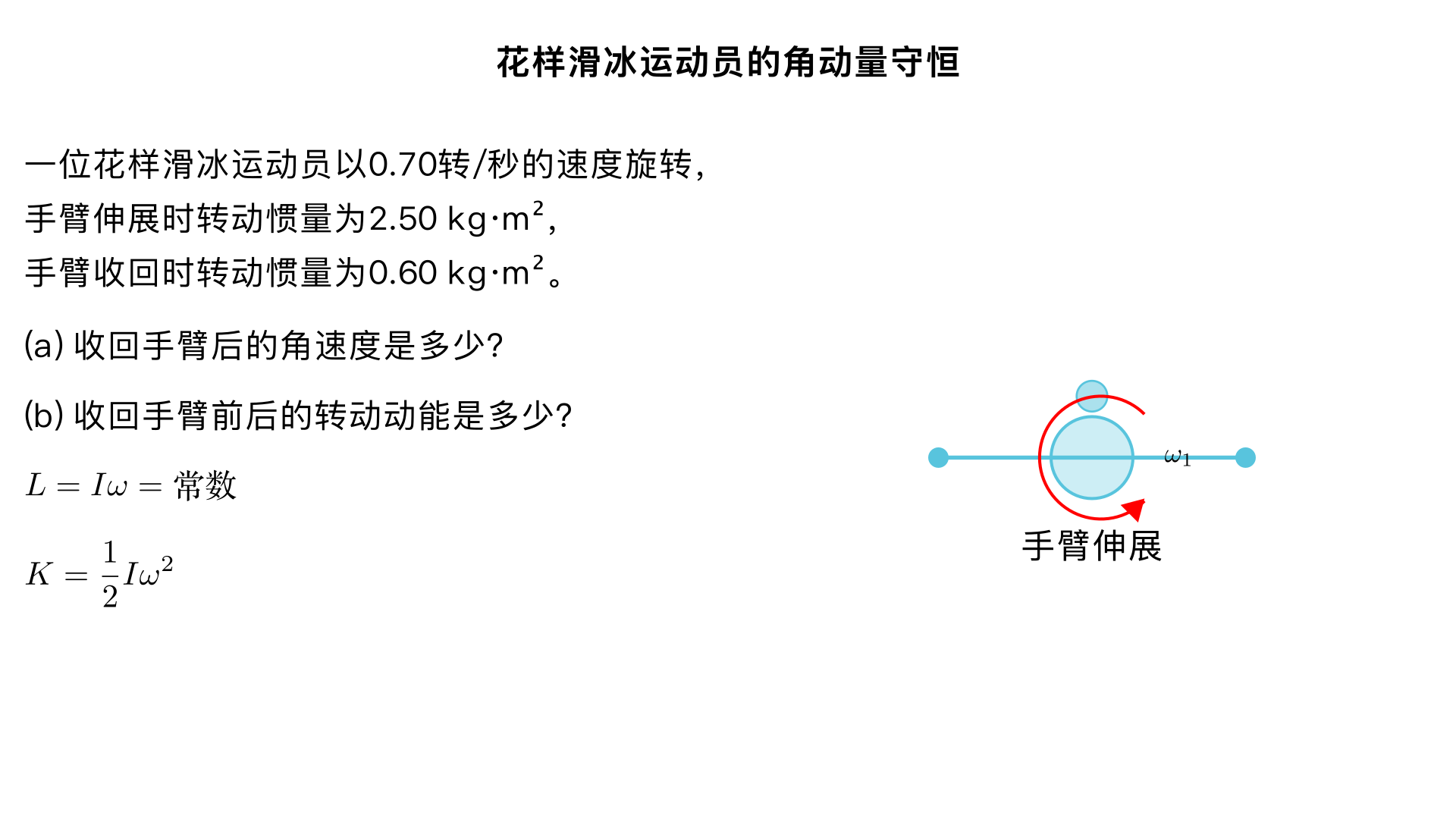
An ice skater is spinning at 0.70 rev/s with her arms extended. She has a moment of inertia of 2.50 kg·m2 with her arms extended and of 0.60 kg·m2 with her arms close to her body. (a) What is her angular velocity in revolutions per second after she pulls in her arms? (b) What is her rotational kinetic energy before and after she does this
▶
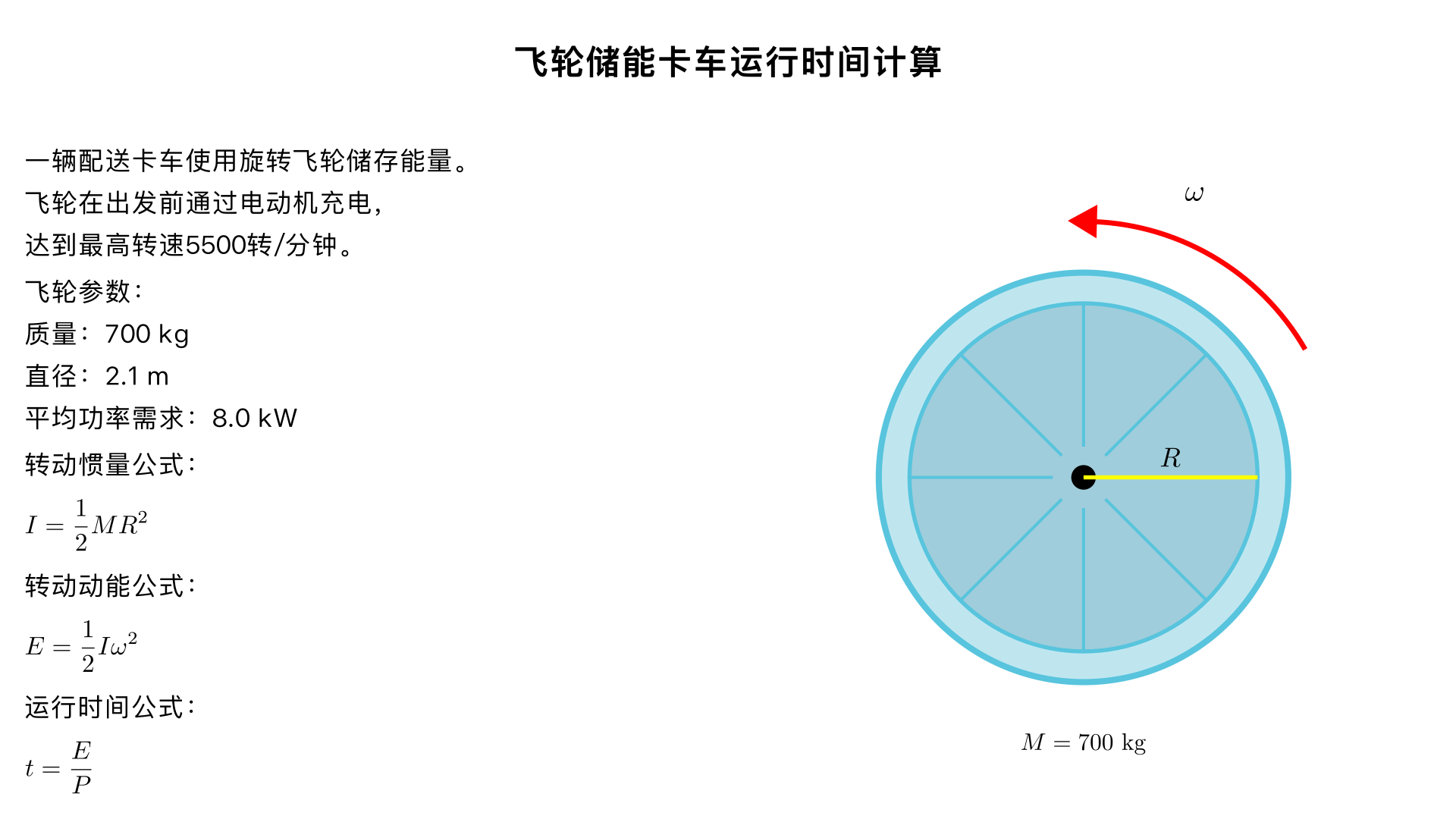
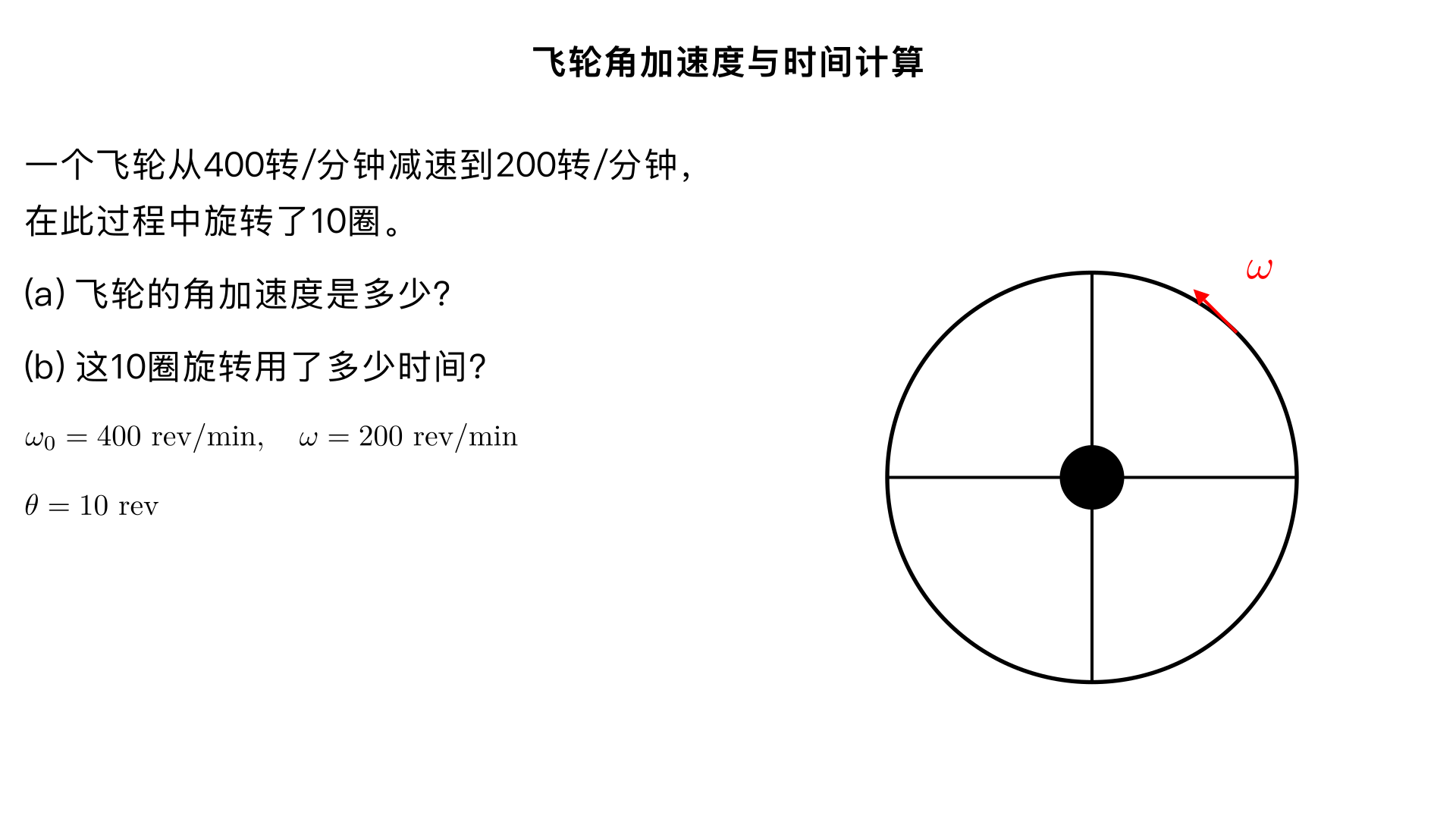
A fleet of delivery trucks operates by making use of the energy stored in a rotating flywheel. The trucks are “charged up” before leaving by using an electric motor to get the flywheel up to its top speed of 5500 revolutions per minute. If one such flywheel is a solid cylinder of mass 700 kg and a diameter of 2.1 m, how long can the truck operate before returning to base for recharging if its average power requirement is 8.0 kilowatts?
▶
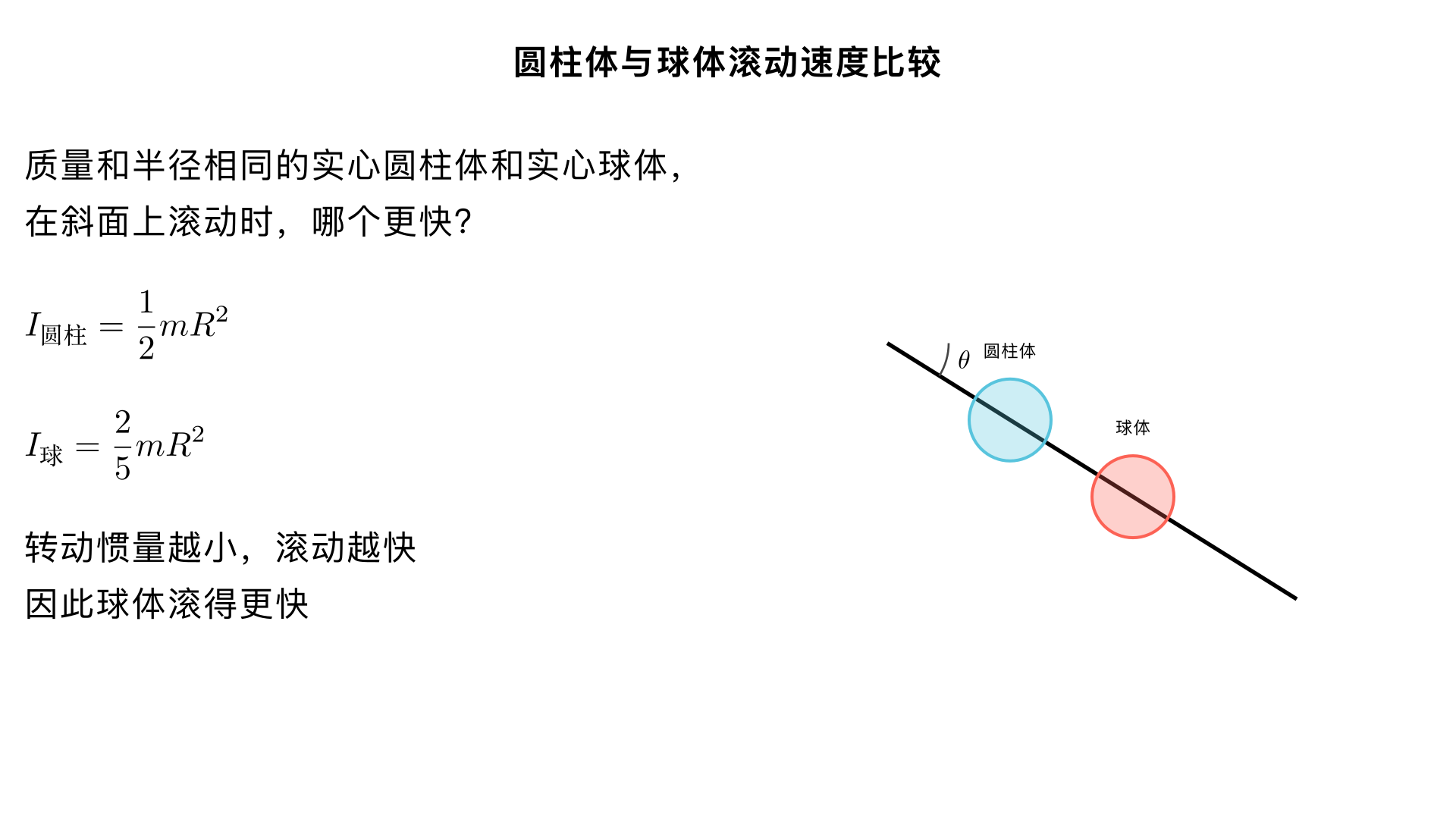
A solid cylinder and a solid sphere have the same mass and radius. Which object will roll down an inclined plane faster and why?
▶