T
Teach Me AnythingTMA
Video History
Page 14 / 44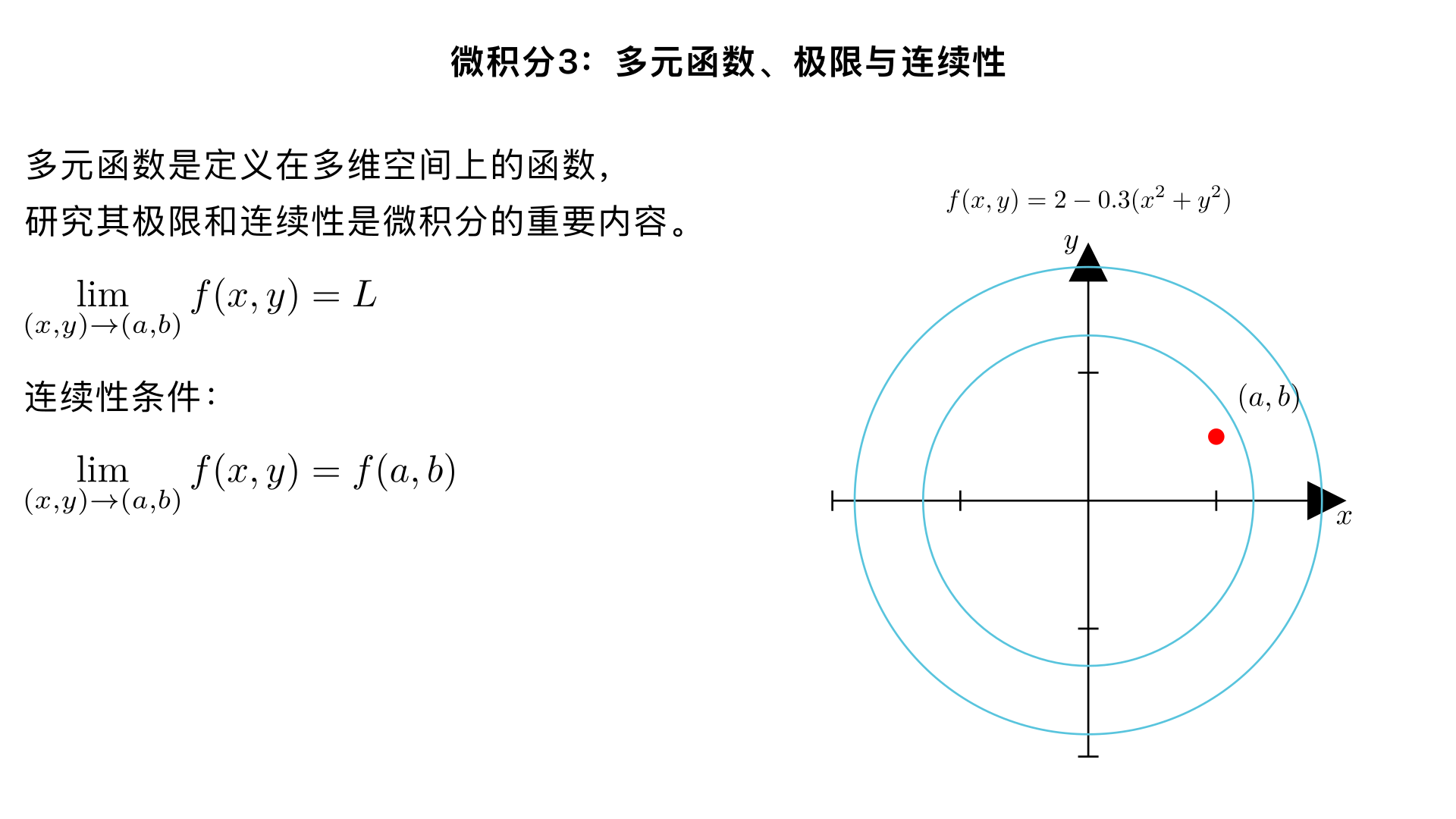
▶
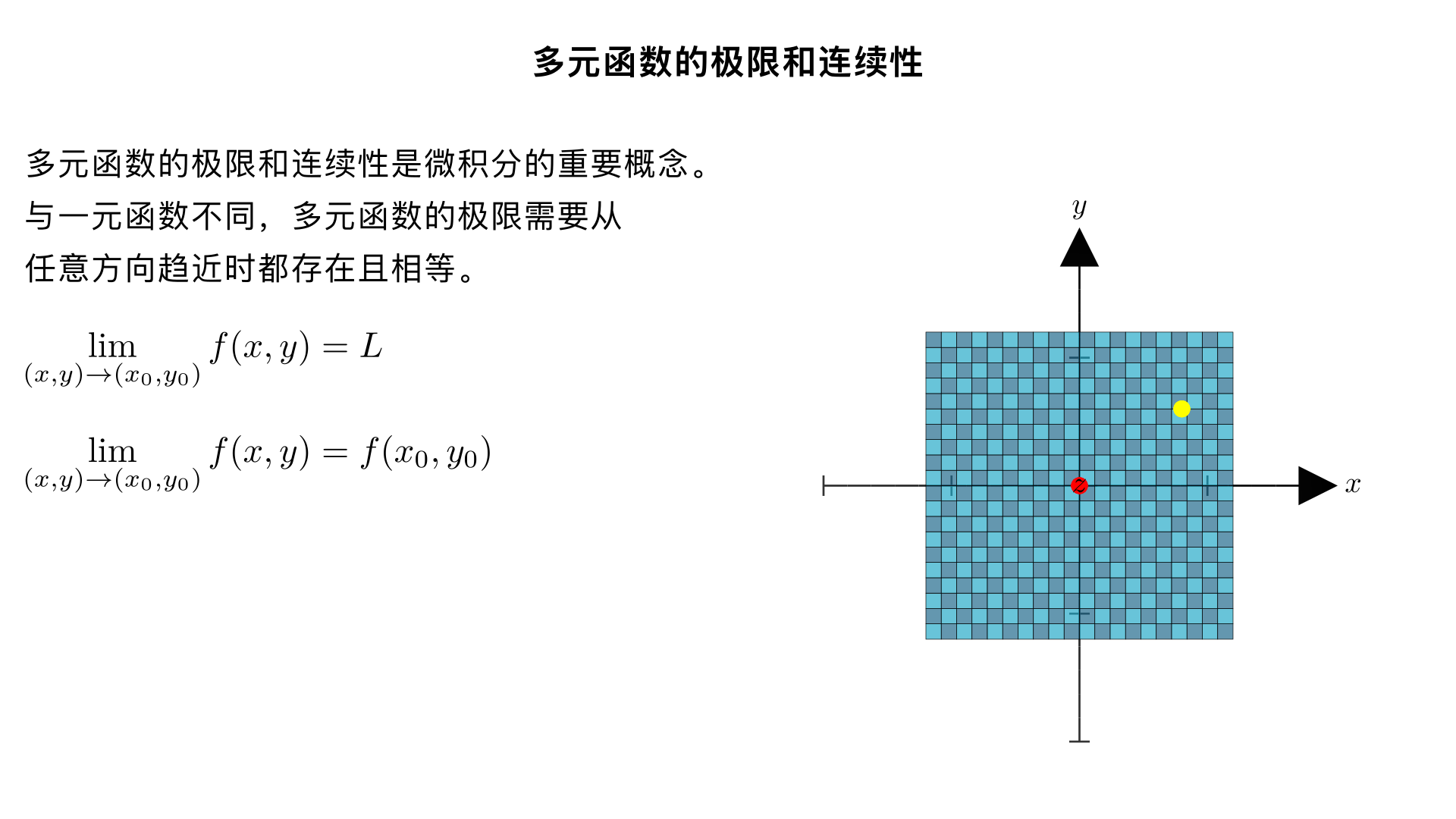
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity

▶
Calculus 3: Multivariable Functions, Limits, and Continuity
▶
微积分 3 多元函数 极限和连续性

▶
### Problem 7 Suppose \( R \) is the relation on \( \mathbb{Z} \times \mathbb{Z} \) where \( aRb \) means that \( a \) has the same lowest order (right-most) digit as \( b \). **Example:** \((a, b) \in R\) when \( a = 1234 \) and \( b = 64 \) because both numbers end in 4. Determine whether \( R \) is an equivalence relation. Show your reasoning. --- ### Solution Yes, \( R \) is an equivalence relation. - **Reflexive:** \( a \) ends with the same digit as itself, so \((a, a) \in R\). - **Symmetric:** If \( a \) ends with the same digit as \( b \), then \( b \) ends with the same digit as \( a \). Thus, if \((a, b) \in R\), then \((b, a) \in R\). - **Transitive:** If \( a \) ends with the same digit as \( b \), and \( b \) ends with the same digit as \( c \), then \( a \) ends with the same digit as \( c \). Hence, \((a, c) \in R\). If asked this on the final, you must show proof of all three required properties.
![### 6. Consider the Turing machine
\[
T = (Q, \Lambda, q_0, \delta)
\]
where:
\[
\begin{aligned}
\delta(q_0, 0) &= (1, R, q_1) \\
\delta(q_0, 1) &= (1, R, q_1) \\
\delta(q_1, 0) &= (1, L, q_0) \\
\delta(q_1, 1) &= (0, R, q_0) \\
\delta(q_0, \#) &= (1, R, q_1) \\
\delta(q_1, \#) &= (\#, R, h)
\end{aligned}
\]
For the following tape, determine the final tape when \(T\) halts, assuming that \(T\) begins in state \(q_0\) at the position indicated by the arrow. Show all steps.
... # # 1 1 0 # # ...
起始箭头在第一个 1 上
使用中文解题](https://manimvideo.explanation.fun/video/cover/590382674076979201.png)
▶
### 6. Consider the Turing machine \[ T = (Q, \Lambda, q_0, \delta) \] where: \[ \begin{aligned} \delta(q_0, 0) &= (1, R, q_1) \\ \delta(q_0, 1) &= (1, R, q_1) \\ \delta(q_1, 0) &= (1, L, q_0) \\ \delta(q_1, 1) &= (0, R, q_0) \\ \delta(q_0, \#) &= (1, R, q_1) \\ \delta(q_1, \#) &= (\#, R, h) \end{aligned} \] For the following tape, determine the final tape when \(T\) halts, assuming that \(T\) begins in state \(q_0\) at the position indicated by the arrow. Show all steps. ... # # 1 1 0 # # ... 起始箭头在第一个 1 上 使用中文解题
![### 5. Consider the following program segment:
```text
i := 1
total := 1
while i < n do
i := i + 1
total := total + i
````
Let
( p ) be the proposition:
[
p:\quad ( \text{total} = \frac{i(i+1)}{2} \ \text{and}\ i \le n )
]
Use mathematical induction to prove ( p ) is a loop invariant.
---
## Solution
### Basis Step
Before the loop is entered, ( p ) is true since
[
\text{total} = 1 = \frac{1(1+1)}{2}
]
and
[
i \le n
]
---
### Inductive Step
Suppose ( p ) is true and ( i = k < n ) after the ( k - 1 )-th execution of the loop.
Since ( p ) is true:
[
\text{total} = \frac{k(k+1)}{2}
]
Suppose that the while loop is executed again. Then ( i ) is incremented to
[
i = k + 1
]
Total becomes:
[
\begin{aligned}
\text{total}
&= \text{total}_{\text{prev}} + i \
&= \frac{k(k+1)}{2} + (k+1) \quad \text{(by inductive hypothesis)} \
&= \frac{k(k+1) + 2(k+1)}{2} \
&= \frac{(k+1)(k+2)}{2}
\end{aligned}
]
---
After the loop, ( i \le n ) and `total` is still of the required form.
Therefore, ( p ) is a loop invariant. ∎
使用中文解答](https://manimvideo.explanation.fun/video/cover/590376661555646465.png)
▶