T
Teach Me AnythingTMA
Video History
Page 15 / 44![### 5. Consider the following program segment:
```text
i := 1
total := 1
while i < n do
i := i + 1
total := total + i
````
Let
( p ) be the proposition:
[
p:\quad ( \text{total} = \frac{i(i+1)}{2} \ \text{and}\ i \le n )
]
Use mathematical induction to prove ( p ) is a loop invariant.
---
## Solution
### Basis Step
Before the loop is entered, ( p ) is true since
[
\text{total} = 1 = \frac{1(1+1)}{2}
]
and
[
i \le n
]
---
### Inductive Step
Suppose ( p ) is true and ( i = k < n ) after the ( k - 1 )-th execution of the loop.
Since ( p ) is true:
[
\text{total} = \frac{k(k+1)}{2}
]
Suppose that the while loop is executed again. Then ( i ) is incremented to
[
i = k + 1
]
Total becomes:
[
\begin{aligned}
\text{total}
&= \text{total}_{\text{prev}} + i \
&= \frac{k(k+1)}{2} + (k+1) \quad \text{(by inductive hypothesis)} \
&= \frac{k(k+1) + 2(k+1)}{2} \
&= \frac{(k+1)(k+2)}{2}
\end{aligned}
]
---
After the loop, ( i \le n ) and `total` is still of the required form.
Therefore, ( p ) is a loop invariant. ∎](https://manimvideo.explanation.fun/video/cover/590376357276651521.png)
▶
### 5. Consider the following program segment: ```text i := 1 total := 1 while i < n do i := i + 1 total := total + i ```` Let ( p ) be the proposition: [ p:\quad ( \text{total} = \frac{i(i+1)}{2} \ \text{and}\ i \le n ) ] Use mathematical induction to prove ( p ) is a loop invariant. --- ## Solution ### Basis Step Before the loop is entered, ( p ) is true since [ \text{total} = 1 = \frac{1(1+1)}{2} ] and [ i \le n ] --- ### Inductive Step Suppose ( p ) is true and ( i = k < n ) after the ( k - 1 )-th execution of the loop. Since ( p ) is true: [ \text{total} = \frac{k(k+1)}{2} ] Suppose that the while loop is executed again. Then ( i ) is incremented to [ i = k + 1 ] Total becomes: [ \begin{aligned} \text{total} &= \text{total}_{\text{prev}} + i \ &= \frac{k(k+1)}{2} + (k+1) \quad \text{(by inductive hypothesis)} \ &= \frac{k(k+1) + 2(k+1)}{2} \ &= \frac{(k+1)(k+2)}{2} \end{aligned} ] --- After the loop, ( i \le n ) and `total` is still of the required form. Therefore, ( p ) is a loop invariant. ∎
![### 4. Given recurrence relation
\[
a_n = -a_{n-1} + n
\]
with initial condition
\[
a_0 = 2
\]
---
### (a) Associated homogeneous recurrence relation
**Solution:**
\[
a_n = -a_{n-1}
\]
---
### (b) General solution to the homogeneous recurrence \((a_n^{(h)})\)
**Solution:**
The characteristic equation has a single root \(-1\), so the general solution is
\[
a_n^{(h)} = \alpha(-1)^n
\]
---
### (c) Particular solution \((a_n^{(p)})\)
**Solution:**
Since the non-homogeneous part is \(n\), assume a particular solution of the form
\[
a_n^{(p)} = cn + d
\]
Substitute into the recurrence relation:
\[
cn + d = -\big(c(n-1) + d\big) + n
\]
\[
= -cn + c - d + n
\]
Rearranging:
\[
2cn - c + 2d - n = 0
\]
\[
n(2c - 1) + (2d - c) = 0
\]
Set each coefficient equal to zero:
\[
2c - 1 = 0 \Rightarrow c = \frac{1}{2}
\]
\[
2d - \frac{1}{2} = 0 \Rightarrow d = \frac{1}{4}
\]
Therefore, the particular solution is
\[
a_n^{(p)} = \frac{1}{2}n + \frac{1}{4}
\]](https://manimvideo.explanation.fun/video/cover/590368266418933761.png)
▶
### 4. Given recurrence relation \[ a_n = -a_{n-1} + n \] with initial condition \[ a_0 = 2 \] --- ### (a) Associated homogeneous recurrence relation **Solution:** \[ a_n = -a_{n-1} \] --- ### (b) General solution to the homogeneous recurrence \((a_n^{(h)})\) **Solution:** The characteristic equation has a single root \(-1\), so the general solution is \[ a_n^{(h)} = \alpha(-1)^n \] --- ### (c) Particular solution \((a_n^{(p)})\) **Solution:** Since the non-homogeneous part is \(n\), assume a particular solution of the form \[ a_n^{(p)} = cn + d \] Substitute into the recurrence relation: \[ cn + d = -\big(c(n-1) + d\big) + n \] \[ = -cn + c - d + n \] Rearranging: \[ 2cn - c + 2d - n = 0 \] \[ n(2c - 1) + (2d - c) = 0 \] Set each coefficient equal to zero: \[ 2c - 1 = 0 \Rightarrow c = \frac{1}{2} \] \[ 2d - \frac{1}{2} = 0 \Rightarrow d = \frac{1}{4} \] Therefore, the particular solution is \[ a_n^{(p)} = \frac{1}{2}n + \frac{1}{4} \]
![**3. Solve this recurrence relation**
\[
a_n = -3a_{n-1} + 18a_{n-2}
\]
with initial conditions
\[
a_0 = 2,\quad a_1 = 9.
\]](https://manimvideo.explanation.fun/video/cover/590354867993411585.png)
▶
**3. Solve this recurrence relation** \[ a_n = -3a_{n-1} + 18a_{n-2} \] with initial conditions \[ a_0 = 2,\quad a_1 = 9. \]
▶
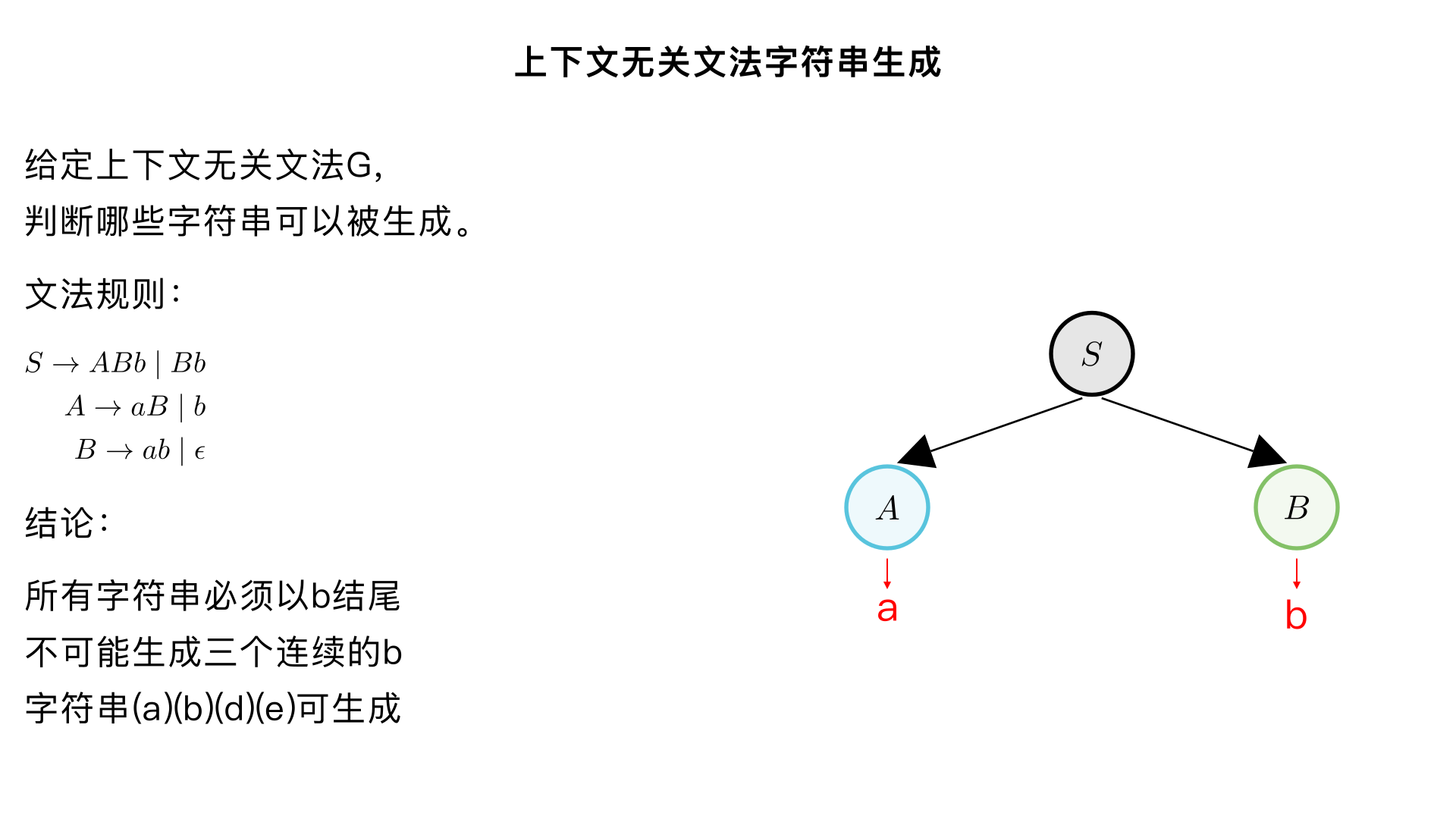
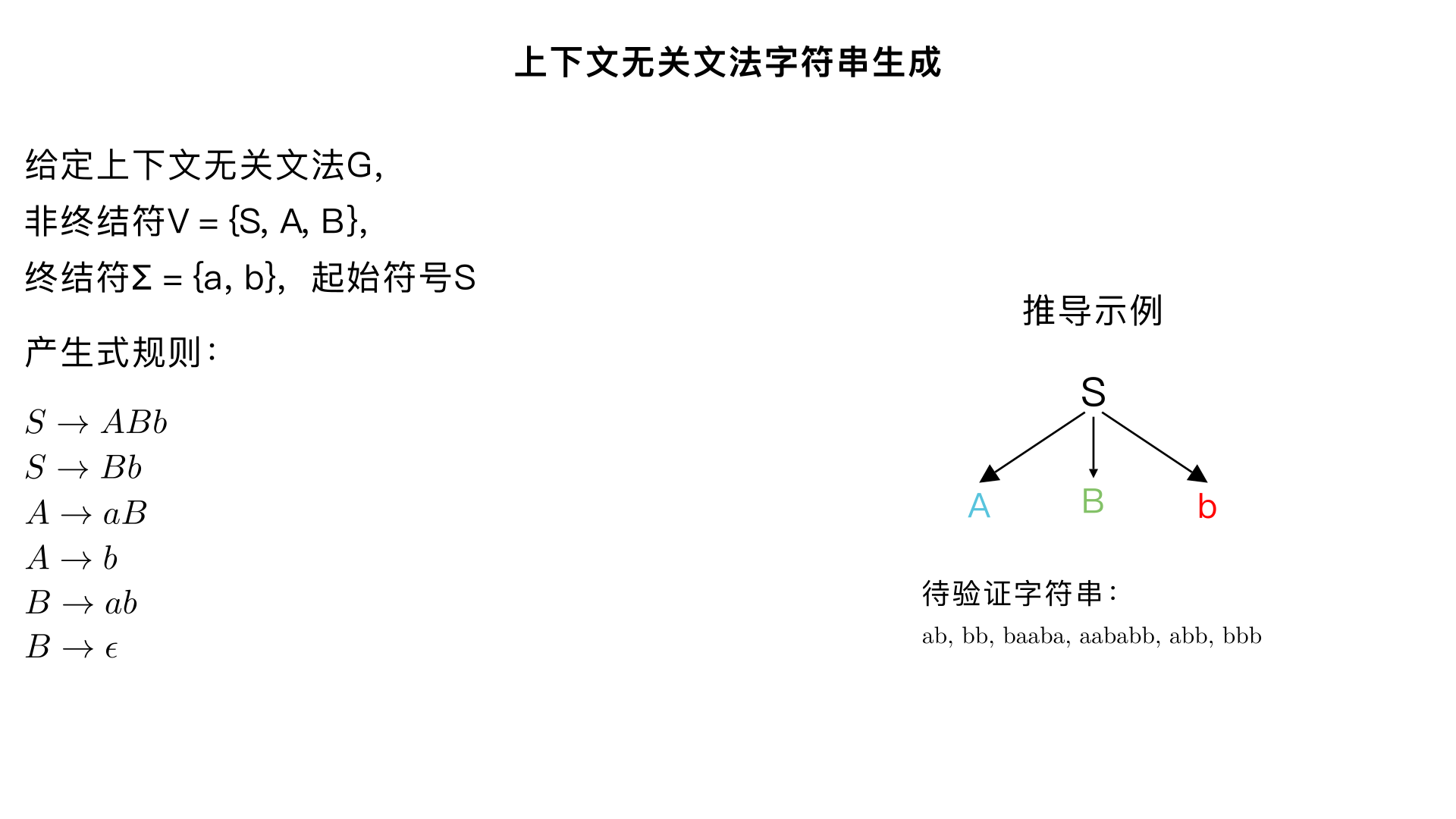
## 2. Let \( G \) be the context-free grammar with non-terminal symbols \( V = \{S, A, B\} \), terminal symbols \( \Sigma = \{a, b\} \), start symbol \( S \), and productions \( P \): - \( S \to ABb \) - \( S \to Bb \) - \( A \to aB \) - \( A \to b \) - \( B \to ab \) - \( B \to \epsilon \) ### Which of these strings can be generated by \( G \)? (a) ab (b) bb (c) baaba (d) aababb (e) abb (f) bbb --- ### Solution All strings must end in **b**, that eliminates **(c)**. It isn’t possible to make three consecutive **b**’s, so **(f)** is eliminated. **(a), (b), (d), and (e)** are all generated by \( G \).
▶
Let G be the context-free grammar with non-terminal symbols V = {S, A, B}, terminal symbols Σ = {a, b}, start symbol S, and productions P: • S → ABb • S → Bb • A → aB • A → b • B → ab • B → ϵ Which of these strings can be generated by G? (a) ab (b) bb (c) baaba (d) aababb (e) abb (f) bbb
▶
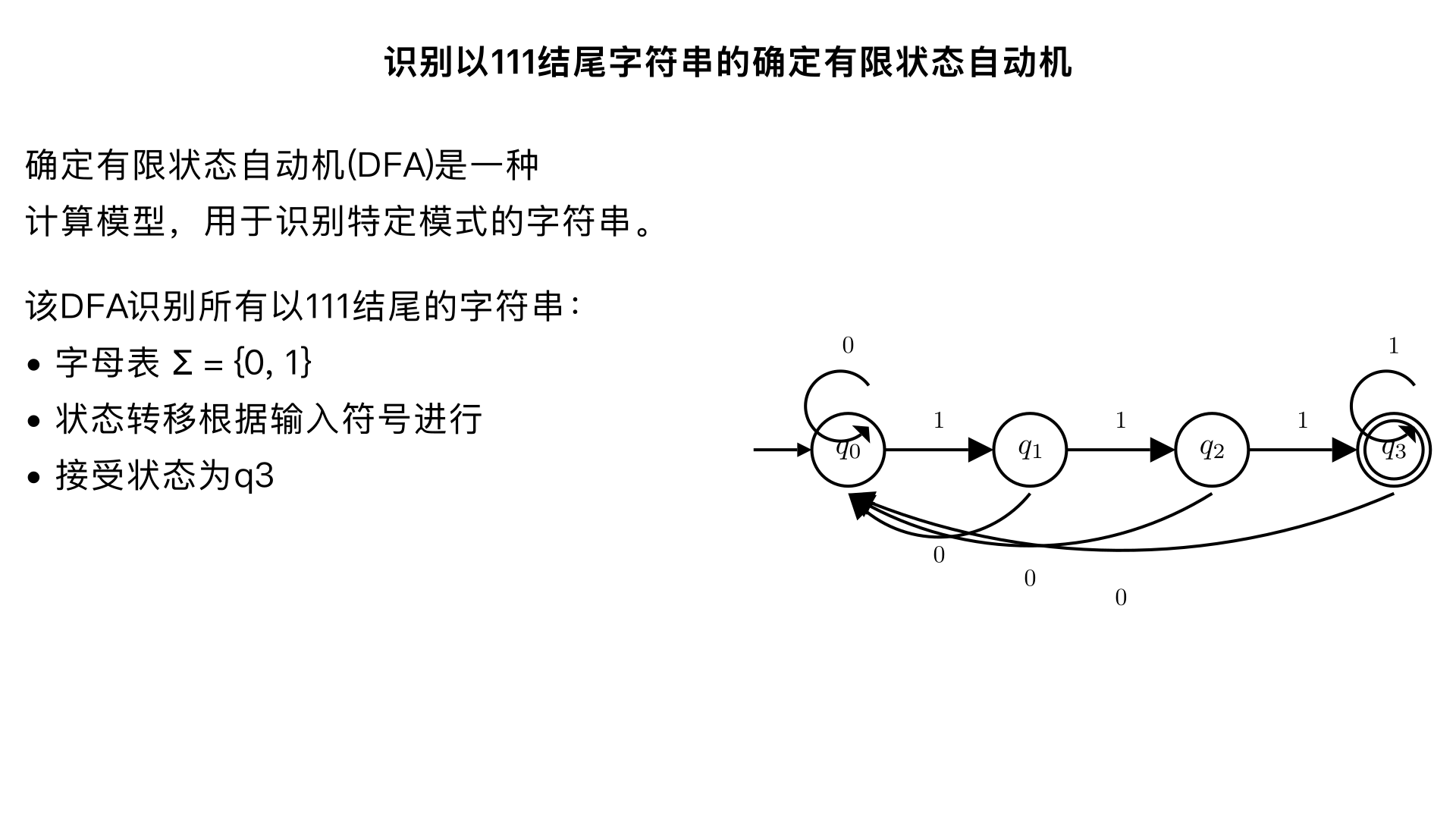
Draw a transition diagram for a deterministic finite-state automaton over Σ = {0, 1} that recognizes any string ending with 111

▶
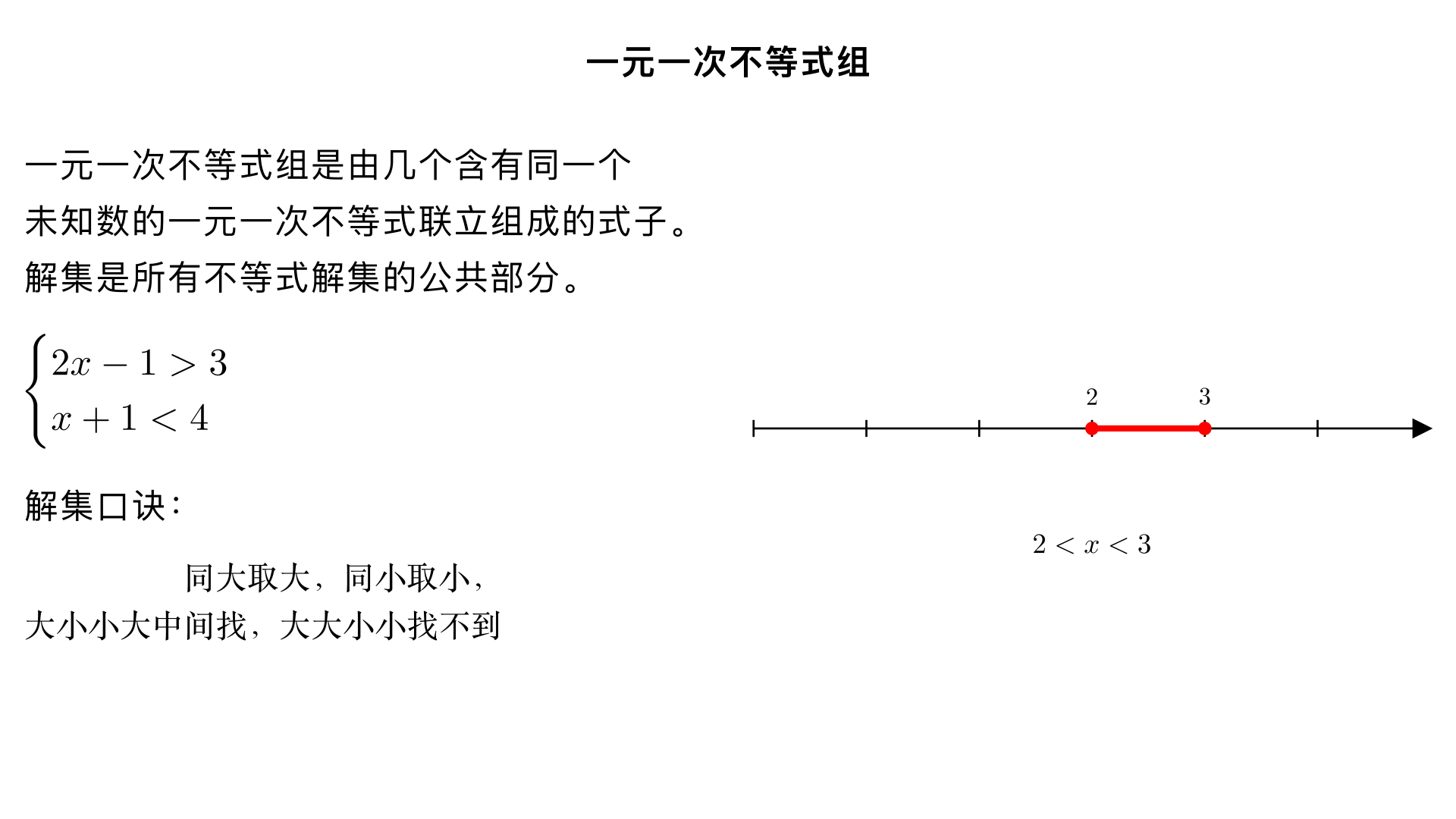
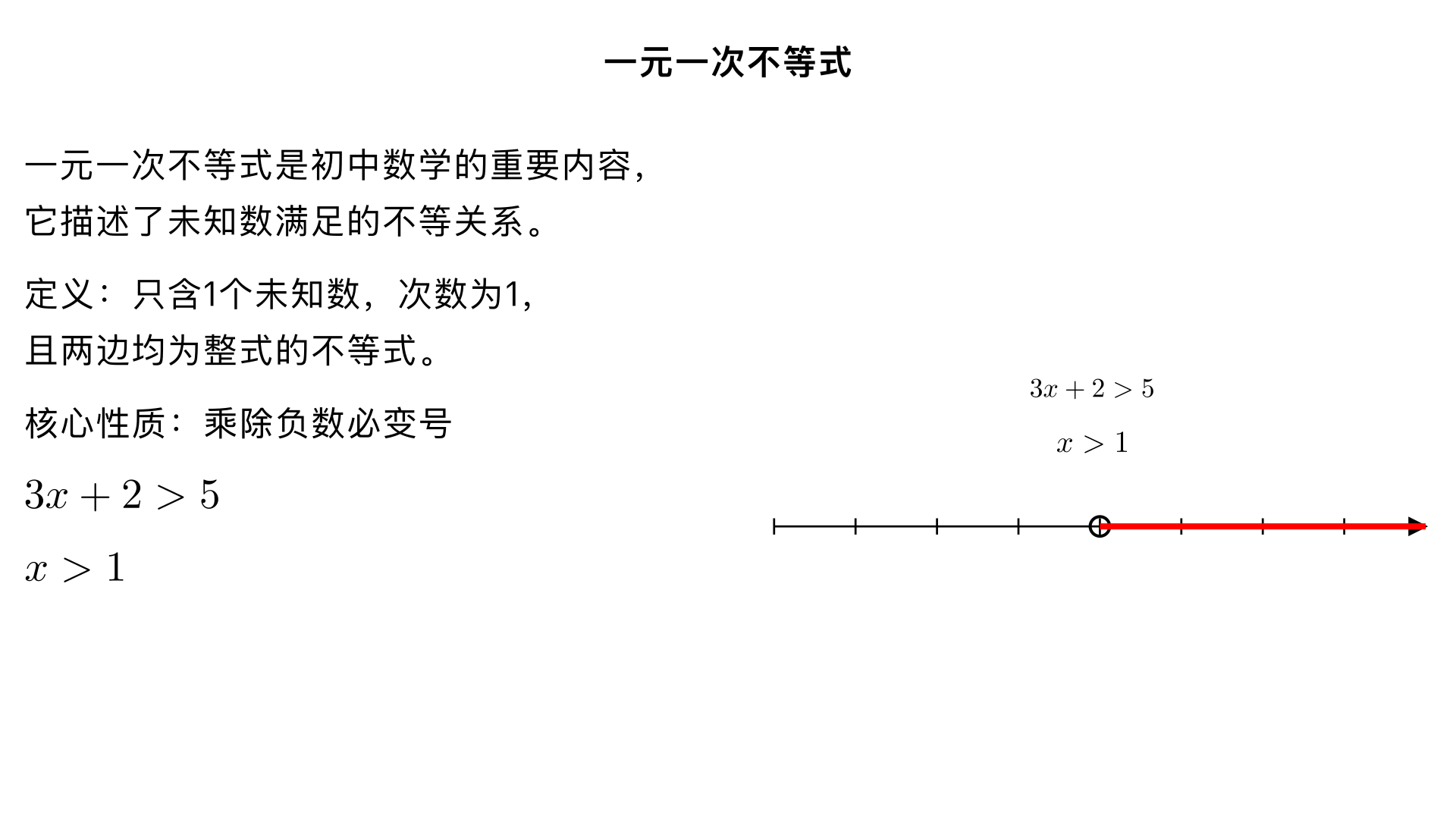
七年级数学 / 不等式与不等式组 / 一元一次不等式 一、核心定义(关键判定条件) 一元一次不等式需同时满足 3 个条件,缺一不可: 只含1 个未知数(如 x、y,仅 1 种); 未知数的次数为 1(无平方、立方等高于 1 次的项); 不等式左右两边均为整式(无分母含未知数、无根号含未知数的情况)。 示例:3x+2>5(符合)、2x²-1≤0(未知数次数 2,不符)、 x 1 +3<2 (分母含未知数,不符) 二、不等式的 3 个核心性质(运算依据,重点记性质 3) 性质 1:加减不变号 不等式两边同时加、减同一个数(或同一个整式),不等号方向不变。 公式:若 a>b,则 a±c > b±c;若 a<b,则 a±c < b±c 示例:5>3 → 5+2>3+2(7>5)、5-4>3-4(1>-1) 性质 2:乘除正数不变号 不等式两边同时乘、除同一个正数,不等号方向不变。 公式:若 a>b、c>0,则 ac > bc、 c a > c b ;若 a<b、c>0,则 ac < bc、 c a < c b 示例:4<6 → 4×2<6×2(8<12)、4÷2<6÷2(2<3) 性质 3:乘除负数必变号(易错点) 不等式两边同时乘、除同一个负数,不等号方向必须改变(> 变 <、≥变≤,反之亦然)。 公式:若 a>b、c<0,则 ac < bc、 c a < c b ;若 a<b、c<0,则 ac> bc、 c a > c b 示例:4<6 → 4×(-2)>6×(-2)(-8>-12)、4÷(-2)>6÷(-2)(-2>-3) 三、不等式的解集与数轴表示(直观呈现解的范围) 1. 解集定义 能使不等式成立的所有未知数的值的集合,叫不等式的解集(区别于 “解”:解是单个值,解集是所有符合条件的值)。 示例:不等式 x+1>3 的解有无数个(x=3、4、5…),解集为 x>2。 2. 数轴表示步骤(3 步到位,不踩错) 画数轴:标注原点、正方向(向右)、单位长度(均匀分段); 定界点:解集含等号(≥、≤)→ 画实心圆点(表示包含该点);解集不含等号(>、<)→ 画空心圆圈(表示不包含该点); 定方向:解集为 “>、≥”→ 从界点向右画射线;解集为 “<、≤”→ 从界点向左画射线。 示例: x>2:数轴上 2 处画空心圆圈,向右画射线; x≤-1:数轴上 - 1 处画实心圆点,向左画射线。 四、解一元一次不等式的 5 步流程(类比一元一次方程,注意变号) 步骤 1:去分母(若有分母) 依据:不等式性质 2、3; 注意:两边同乘所有分母的最小公倍数,别漏乘 “不含分母的项”;若分母为负数,乘完后需按性质 3 改变不等号方向。 示例: 2 x +1>3 → 两边乘 2:x + 2 > 6(无漏乘,分母为正,不变号)。 步骤 2:去括号(若有括号) 依据:乘法分配律(a (b±c)=ab±ac); 注意:括号前是负号,去括号后括号内所有项需变号(正变负、负变正)。 示例:2 (x-3)+1≤5 → 去括号:2x - 6 + 1 ≤ 5。 步骤 3:移项(含未知数的项移左,常数项移右) 依据:不等式性质 1; 注意:移项的项需变号(移左变右、正变负、负变正),未移项的项不变号。 示例:2x - 6 + 1 ≤ 5 → 移项:2x ≤ 5 + 6 - 1(-6、+1 移右变 + 6、-1)。 步骤 4:合并同类项 依据:合并同类项法则(同类项系数相加,字母及次数不变); 左右两边分别合并,简化为 “ax>b”“ax<b”“ax≥b”“ax≤b”(a≠0)的形式。 示例:2x ≤ 5 + 6 - 1 → 合并:2x ≤ 10。 步骤 5:系数化为 1(求最终解集) 依据:不等式性质 2、3; 注意:两边同除以未知数的系数 a: 若 a>0:不等号方向不变; 若 a<0:不等号方向必须改变。 示例:2x ≤ 10(a=2>0,不变号)→ x ≤ 5;-3x>6(a=-3<0,变号)→ x<-2。 五、常见易错点总结(避坑关键) 去分母漏乘:忘记乘 “不含分母的常数项”(如 3 x −2>1 ,漏乘 2 得 x-2>3,错误); 乘除负数忘变号:系数化为 1 时,a<0 却不换不等号方向(如 - 2x≤4,错解 x≤-2,正解 x≥-2); 界点标注错误:含等号画空心、不含等号画实心(如 x≥3 画空心,错误); 射线方向颠倒:“>” 向左画、“<” 向右画(如 x>1 向左画,错误)。(五分钟以内视频)
▶
七年级数学:数据的收集、整理与描述 —— 统计调查 一、统计调查的基本概念 总体:要考察的全体对象个体:组成总体的每一个考察对象样本:从总体中抽取的一部分个体样本容量:样本中个体的数目(不带单位) 二、调查方式 1. 全面调查(普查) 定义:考察全体对象的调查 适用场景: 调查范围小、对象数量少 精确度要求高、事关重大 如:班级同学身高调查、飞船零部件检查 2. 抽样调查 定义:只抽取部分对象进行调查,根据样本推断总体 适用场景: 调查对象数量庞大 调查具有破坏性 如:灯泡使用寿命测试、水质调查 3. 调查方式选择原则 情况 建议调查方式 原因 范围小、易操作 全面调查 数据准确、全面 范围大、数量多 抽样调查 节省人力物力 具有破坏性 抽样调查 避免全部损坏 精确度要求高 全面调查 确保结果准确 三、统计调查的一般步骤 确定调查问题:明确要研究什么 确定调查对象:明确研究的总体 选择调查方法:全面调查或抽样调查 设计调查问卷:设计合理的问题收集数据 收集数据:通过问卷、访谈等方式获取数据 整理数据:使用划记法("正" 字计数)统计数据 描述数据:用统计表、统计图展示结果 分析数据,得出结论:解读数据,提出建议 四、数据收集方法 1. 问卷调查法 设计要点:问题明确、选项互斥、便于统计 例:"你最喜欢的运动是:A. 篮球 B. 足球 C. 羽毛球 D. 其他" 2. 其他收集方法 访问调查:面对面交流获取信息 实地调查:直接观察记录数据 媒体调查:通过报纸、网络等收集现成数据 五、数据整理方法 划记法("正" 字计数法) 每个 "正" 字代表 5 个数据 步骤: 列出所有类别 逐一读取数据,在对应类别下画 "正" 字 统计 "正" 字数量,计算总数 频数与频率 频数:落在各小组内的数据个数 频率:频数 ÷ 数据总数(所有频率之和为 1) 公式:频率 = 频数 ÷ 总数,频数 = 频率 × 总数 六、数据描述方法 1. 统计表 将数据按类别整理成表格,清晰展示数量关系 优点:数据准确、可详细记录信息 缺点:不够直观 2. 统计图(重点) (1)条形统计图 特点:用等宽条形的高度表示数据多少,便于比较 适用场景:比较不同类别数据的大小 制作步骤: 画两条互相垂直的数轴(横轴表示类别,纵轴表示数量) 根据数据大小确定单位长度 画出对应高度的条形,宽度一致,间隔相等 (2)扇形统计图 特点:用圆代表总体,扇形大小表示各部分占比 适用场景:展示各部分在总体中所占百分比 制作关键: 计算各部分百分比:(部分数量 ÷ 总数)×100% 计算圆心角度数:百分比 ×360° 用量角器画出对应扇形 (3)折线统计图 特点:用折线起伏表示数据变化趋势 适用场景:反映数据随时间或顺序的变化规律 制作步骤: 建立坐标系(横轴表示时间 / 顺序,纵轴表示数量) 标出数据点 用线段依次连接各点 3. 统计图选择标准 比较数据大小:选条形图 展示比例关系:选扇形图 反映变化趋势:选折线图 七、典型例题 例 1:调查方式选择 下列调查中,适合全面调查的是( )A. 了解某品牌灯泡的使用寿命B. 调查全班同学的视力情况C. 了解某市中学生的课外阅读情况D. 检测某批次汽车的抗撞击能力 答案:B(A、C、D 适合抽样调查,B 范围小,适合全面调查) 例 2:总体、个体、样本、样本容量 为了解某校七年级 200 名学生的身高情况,从中抽取 50 名学生测量身高。 总体:该校七年级 200 名学生的身高个体:每名七年级学生的身高样本:抽取的 50 名学生的身高样本容量:50 例 3:数据整理与描述 某班对 "最喜欢的水果" 进行调查,结果如下:苹果:正正正香蕉:正正橙子:正其他:正 (1)该班共有多少人?(2)喜欢苹果的频率是多少? 解:(1)总人数 = 3×5 + 2×5 + 1×5 + 1×5 = 35(人)(2)喜欢苹果的频率 = 15÷35 ≈ 0.429(或 42.9%) 八、总结与应用 核心要点: 统计调查是收集、整理、分析数据的基础方法 掌握两种调查方式的选择与应用场景 学会设计问卷、整理数据(划记法)和选择合适的统计图描述数据 实际应用:统计调查在生活中广泛应用,如市场调研、健康调查、民意测验等。掌握统计调查方法,有助于我们科学分析问题,做出合理决策。 学习建议: 选择一个感兴趣的话题(如班级同学的爱好、家庭用水量等),亲自设计并实施一次简单的统计调查 练习根据不同数据特点选择合适的统计图进行描述
▶
一元一次不等式组 一、基本概念 定义:由几个含有同一个未知数的一元一次不等式联立组成的式子,叫做一元一次不等式组。 关键条件: 每个不等式必须是一元一次不等式(只含一个未知数,且未知数次数为 1) 所有不等式必须含有同一个未知数 不等式组中至少有两个不等式 解集:不等式组中所有不等式解集的公共部分,叫做这个不等式组的解集。如果没有公共部分,则称不等式组无解。 二、不等式的基本性质(解不等式的依据) 性质 1:不等式两边加(或减)同一个数(或式子),不等号方向不变。若 a > b,则 a ± c > b ± c 性质 2:不等式两边乘(或除以)同一个正数,不等号方向不变。若 a > b,c > 0,则 ac > bc(或 a/c > b/c) 性质 3:不等式两边乘(或除以)同一个负数,不等号方向改变。若 a > b,c < 0,则 ac < bc(或 a/c < b/c) 三、一元一次不等式组的解法 1. 解法步骤 步骤 1:分别求出不等式组中每个不等式的解集步骤 2:将每个不等式的解集在同一个数轴上表示出来步骤 3:利用数轴找出这些解集的公共部分,即为不等式组的解集 2. 解集确定口诀(简化判断) 不等式组形式 解集 口诀 x > a x > b (a < b) x > b 同大取大 x < a x < b (a < b) x < a 同小取小 x > a x < b (a < b) a < x < b 大小小大中间找 x < a x > b (a < b) 无解 大大小小找不到 前提:不等式已化为最简形式 3. 例题解析 例 1:解不等式组 plaintext { 2x - 1 > 3 ① x + 1 < 4 ② } 解: 解不等式①:2x - 1 > 3 → 2x > 4 → x > 2 解不等式②:x + 1 < 4 → x < 3 在数轴上表示两个解集(略) 公共部分为:2 < x < 3 例 2:解不等式组 plaintext { x + 2 ≥ 5 ① 3x - 1 > 8 ② } 解: 解①:x ≥ 3 解②:3x > 9 → x > 3 公共部分:x > 3(同大取大) 四、一元一次不等式组的解集表示方法 1. 不等式表示法 如:2 < x < 3,x ≥ 5 2. 数轴表示法(直观、常用) 画数轴,标出关键点 大于(>)或小于(<)用空心圆圈表示不包含该点 大于等于(≥)或小于等于(≤)用实心圆点表示包含该点 用线段或射线表示解集范围 五、一元一次不等式组的应用 解题步骤: 设未知数 根据题意找出不等关系(关键词:至少、最多、不超过、不少于等) 列出不等式组 解不等式组 根据实际问题确定答案(注意是否取整数等) 典型应用题类型: 分配问题:如分苹果、安排座位等 行程问题:如速度、时间、路程关系 经济问题:如购物优惠、成本利润 方案设计:如选择最佳方案、购买计划 积分问题:如比赛得分、考试成绩 例:小华家距学校 2.4 千米,走到一半时发现只剩 12 分钟到校。问:他走剩下路程的平均速度至少要多少? 解: 设速度至少为 x 千米 / 分钟 剩余路程 1.2 千米,时间≤12 分钟 不等关系:1.2/x ≤ 12 → x ≥ 0.1 答:平均速度至少要0.1 千米 / 分钟(或 6 千米 / 小时) 六、总结与要点 定义:含同一未知数的多个一元一次不等式的组合 解法:先分别求解,再找公共部分(数轴或口诀) 口诀:同大取大,同小取小,大小小大中间找,大大小小找不到 应用:关键是找出实际问题中的不等关系
▶
七年级数学 / 不等式与不等式组 / 一元一次不等式 一、核心定义(关键判定条件) 一元一次不等式需同时满足 3 个条件,缺一不可: 只含1 个未知数(如 x、y,仅 1 种); 未知数的次数为 1(无平方、立方等高于 1 次的项); 不等式左右两边均为整式(无分母含未知数、无根号含未知数的情况)。 示例:3x+2>5(符合)、2x²-1≤0(未知数次数 2,不符)、 x 1 +3<2 (分母含未知数,不符) 二、不等式的 3 个核心性质(运算依据,重点记性质 3) 性质 1:加减不变号 不等式两边同时加、减同一个数(或同一个整式),不等号方向不变。 公式:若 a>b,则 a±c > b±c;若 a<b,则 a±c < b±c 示例:5>3 → 5+2>3+2(7>5)、5-4>3-4(1>-1) 性质 2:乘除正数不变号 不等式两边同时乘、除同一个正数,不等号方向不变。 公式:若 a>b、c>0,则 ac > bc、 c a > c b ;若 a<b、c>0,则 ac < bc、 c a < c b 示例:4<6 → 4×2<6×2(8<12)、4÷2<6÷2(2<3) 性质 3:乘除负数必变号(易错点) 不等式两边同时乘、除同一个负数,不等号方向必须改变(> 变 <、≥变≤,反之亦然)。 公式:若 a>b、c<0,则 ac < bc、 c a < c b ;若 a<b、c<0,则 ac> bc、 c a > c b 示例:4<6 → 4×(-2)>6×(-2)(-8>-12)、4÷(-2)>6÷(-2)(-2>-3) 三、不等式的解集与数轴表示(直观呈现解的范围) 1. 解集定义 能使不等式成立的所有未知数的值的集合,叫不等式的解集(区别于 “解”:解是单个值,解集是所有符合条件的值)。 示例:不等式 x+1>3 的解有无数个(x=3、4、5…),解集为 x>2。 2. 数轴表示步骤(3 步到位,不踩错) 画数轴:标注原点、正方向(向右)、单位长度(均匀分段); 定界点:解集含等号(≥、≤)→ 画实心圆点(表示包含该点);解集不含等号(>、<)→ 画空心圆圈(表示不包含该点); 定方向:解集为 “>、≥”→ 从界点向右画射线;解集为 “<、≤”→ 从界点向左画射线。 示例: x>2:数轴上 2 处画空心圆圈,向右画射线; x≤-1:数轴上 - 1 处画实心圆点,向左画射线。 四、解一元一次不等式的 5 步流程(类比一元一次方程,注意变号) 步骤 1:去分母(若有分母) 依据:不等式性质 2、3; 注意:两边同乘所有分母的最小公倍数,别漏乘 “不含分母的项”;若分母为负数,乘完后需按性质 3 改变不等号方向。 示例: 2 x +1>3 → 两边乘 2:x + 2 > 6(无漏乘,分母为正,不变号)。 步骤 2:去括号(若有括号) 依据:乘法分配律(a (b±c)=ab±ac); 注意:括号前是负号,去括号后括号内所有项需变号(正变负、负变正)。 示例:2 (x-3)+1≤5 → 去括号:2x - 6 + 1 ≤ 5。 步骤 3:移项(含未知数的项移左,常数项移右) 依据:不等式性质 1; 注意:移项的项需变号(移左变右、正变负、负变正),未移项的项不变号。 示例:2x - 6 + 1 ≤ 5 → 移项:2x ≤ 5 + 6 - 1(-6、+1 移右变 + 6、-1)。 步骤 4:合并同类项 依据:合并同类项法则(同类项系数相加,字母及次数不变); 左右两边分别合并,简化为 “ax>b”“ax<b”“ax≥b”“ax≤b”(a≠0)的形式。 示例:2x ≤ 5 + 6 - 1 → 合并:2x ≤ 10。 步骤 5:系数化为 1(求最终解集) 依据:不等式性质 2、3; 注意:两边同除以未知数的系数 a: 若 a>0:不等号方向不变; 若 a<0:不等号方向必须改变。 示例:2x ≤ 10(a=2>0,不变号)→ x ≤ 5;-3x>6(a=-3<0,变号)→ x<-2。 五、常见易错点总结(避坑关键) 去分母漏乘:忘记乘 “不含分母的常数项”(如 3 x −2>1 ,漏乘 2 得 x-2>3,错误); 乘除负数忘变号:系数化为 1 时,a<0 却不换不等号方向(如 - 2x≤4,错解 x≤-2,正解 x≥-2); 界点标注错误:含等号画空心、不含等号画实心(如 x≥3 画空心,错误); 射线方向颠倒:“>” 向左画、“<” 向右画(如 x>1 向左画,错误)。
▶
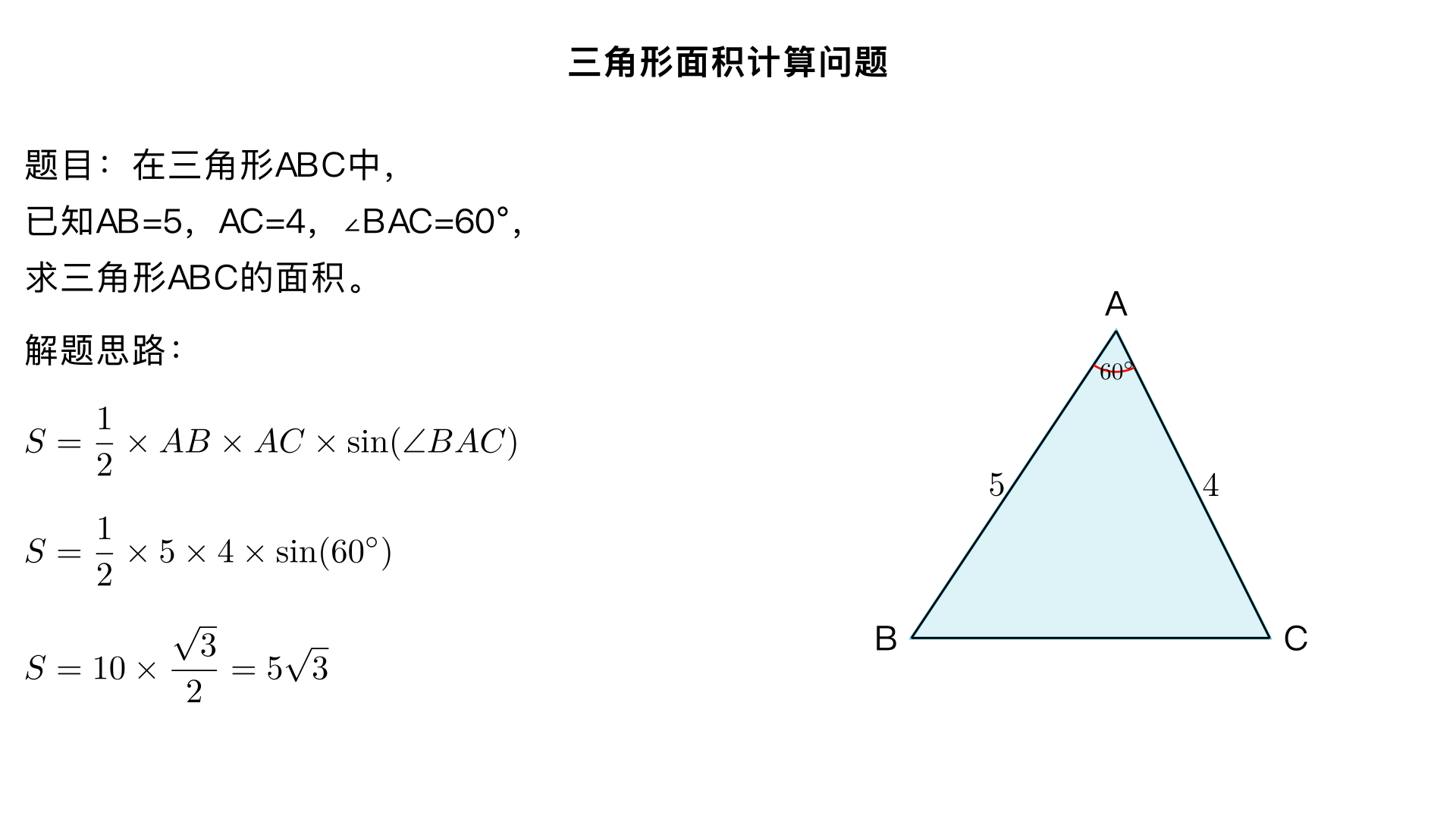
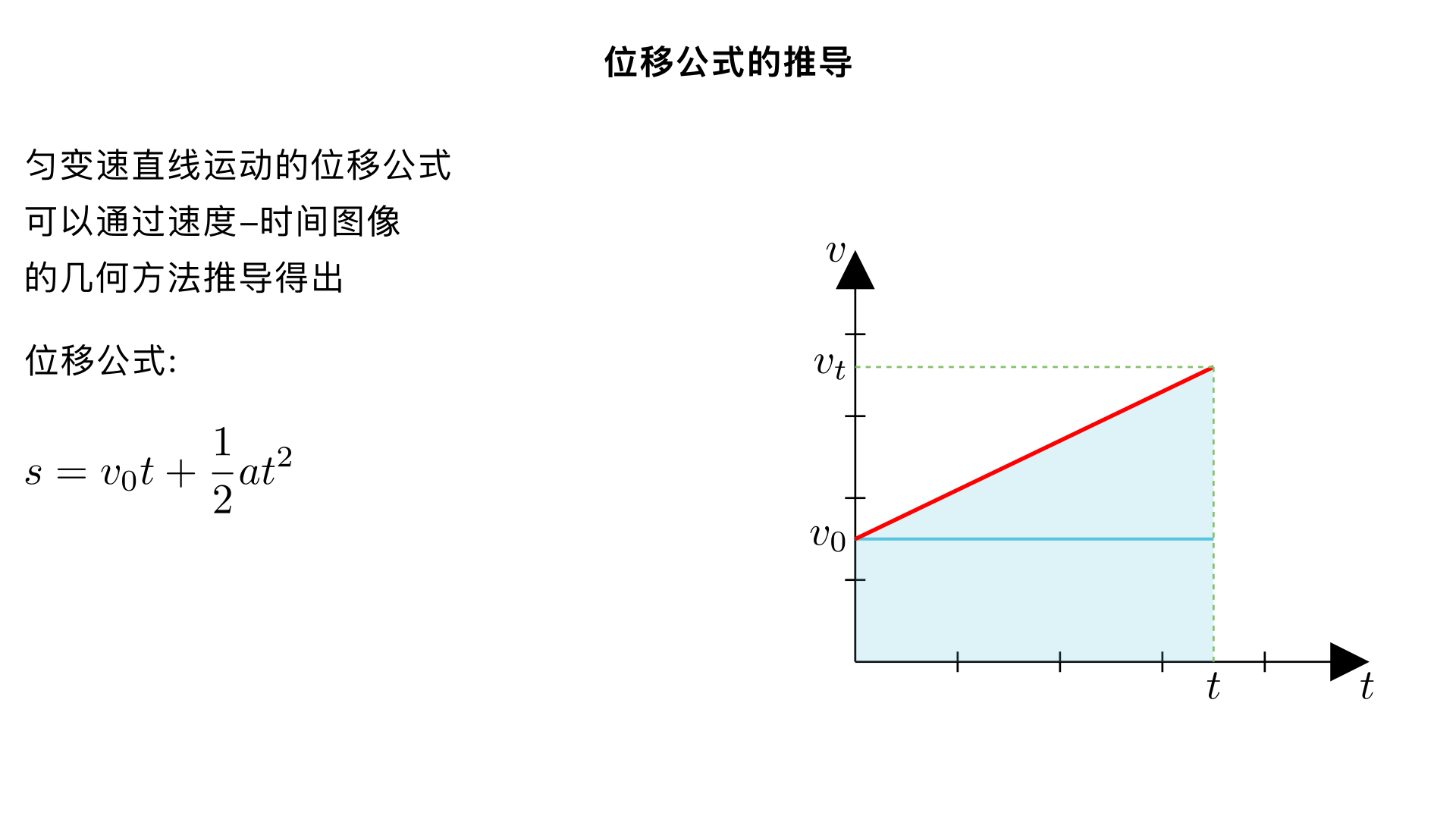
讲解图片中题目
▶