T
Teach Me AnythingTMA
Video History
Page 26 / 44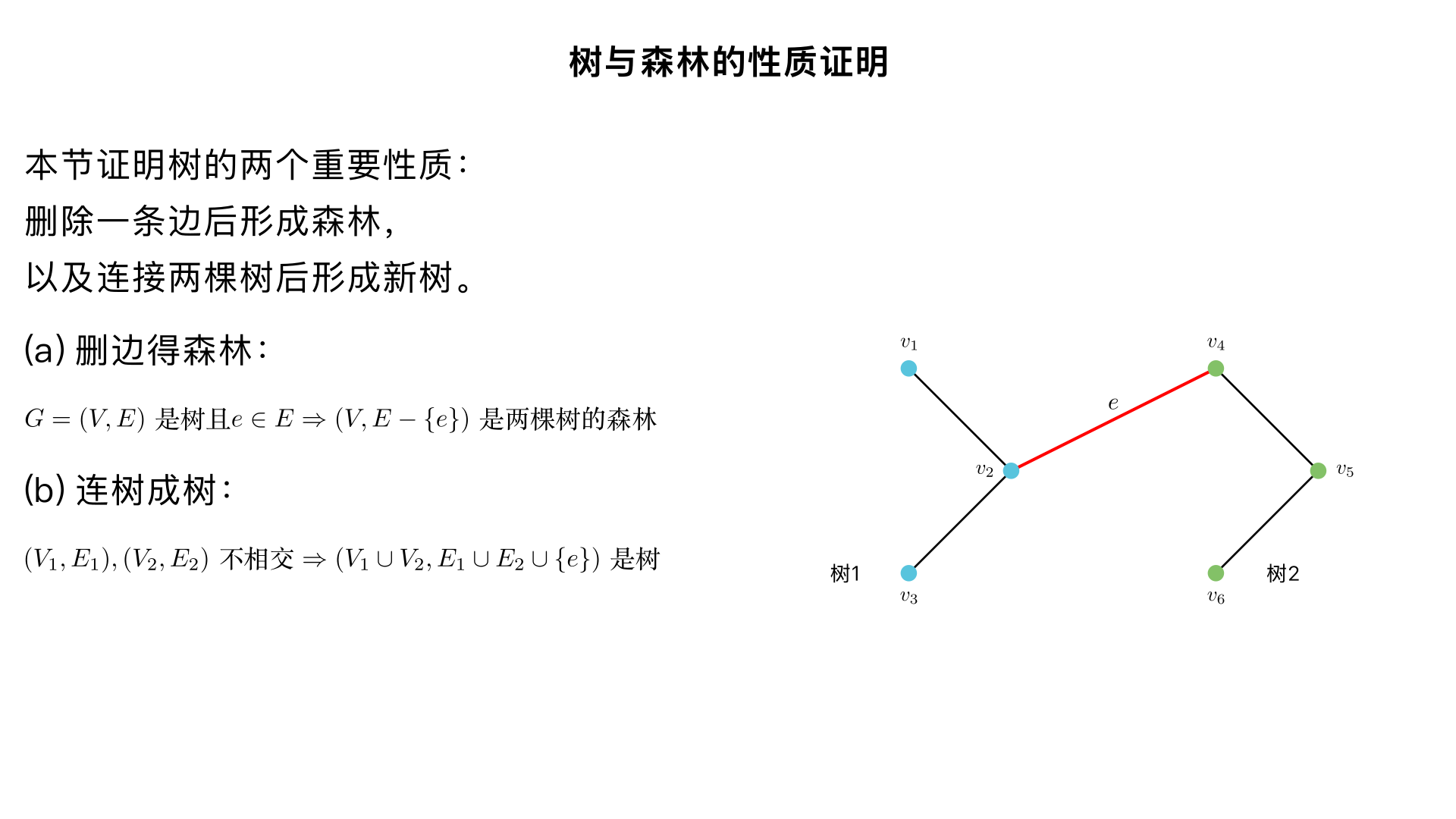
▶
(a) 证明:如果 ( G = (V, E) ) 是一棵树且 ( e \in E ),那么 ( (V, E - {e}) ) 是由两棵树组成的森林。 (b) 证明:如果 ( (V_1, E_1) ) 和 ( (V_2, E_2) ) 是不相交的两棵树,并且 ( e ) 是一条连接 ( V_1 ) 中某个顶点与 ( V_2 ) 中某个顶点的边,那么 ( (V_1 \cup V_2, E_1 \cup E_2 \cup {e}) ) 是一棵树。
▶
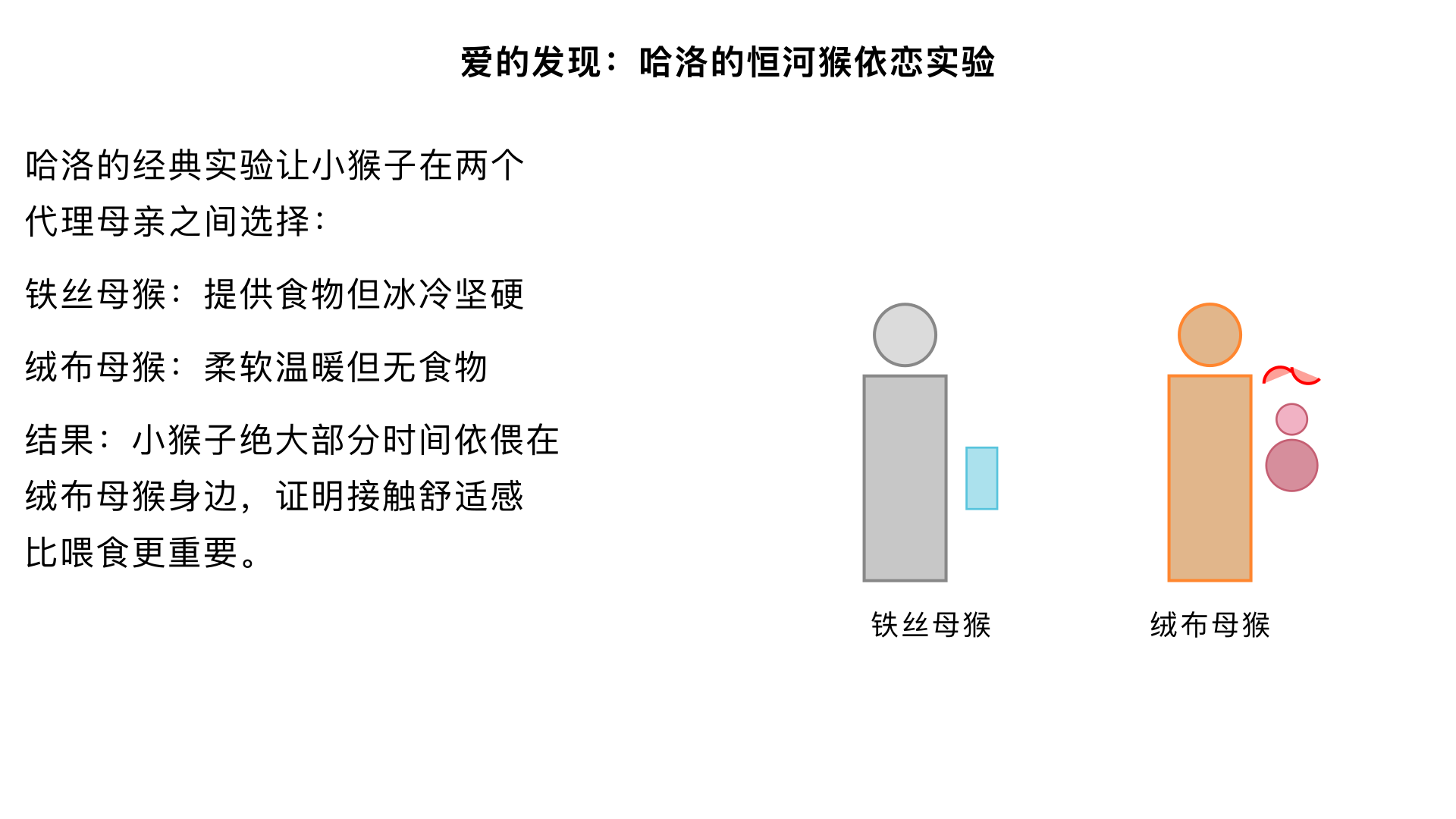
17、爱的发现 (哈洛的“恒河猴依恋”实验) 主要内容:让小猴子在“铁丝母猴”和“绒布母猴”之间选择,尽管只有铁丝母猴提供食物,小猴子仍绝大部分时间依偎在绒布母猴身边。这项研究颠覆了“有奶便是娘”的观点,证明了接触舒适感是形成依恋的关键,比喂食更重要。

▶
16、心中的成长 (皮亚杰的“认知发展理论”) 主要内容:通过一系列巧妙的实验,揭示了儿童的思维并非成人思维的简化版,而是遵循一个通过“同化”和“顺应”不断建构的、有阶段的(感知运动阶段、前运算阶段等)发展过程。
▶
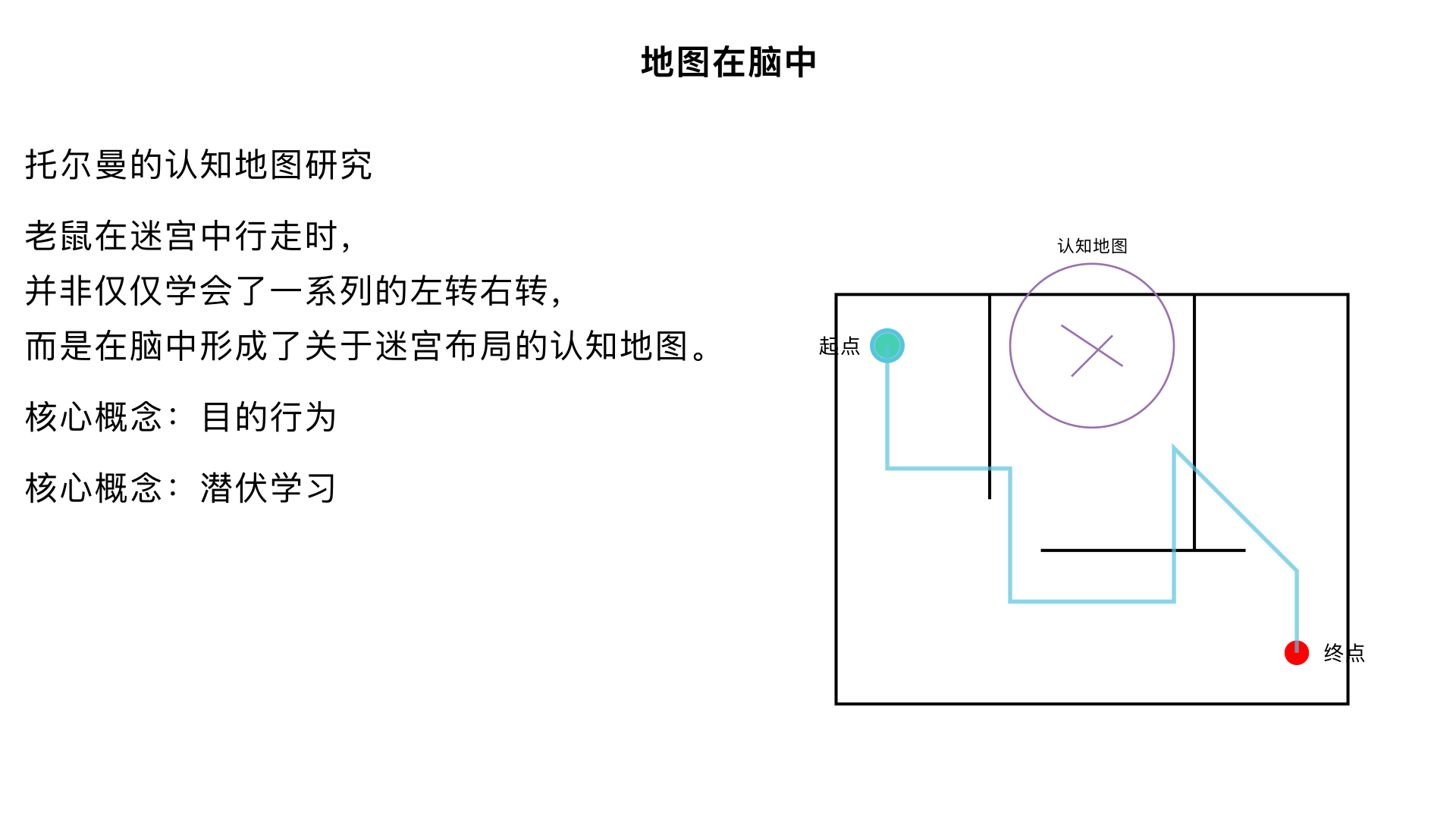
15、地图在脑中 (托尔曼的“认知地图”研究) 主要内容:发现老鼠在迷宫中行走时,并非仅仅学会了一系列的“左转右转”(刺激-反应联结),而是在脑中形成了关于迷宫布局的“认知地图”。这挑战了严格的行为主义观点,引入了“目的行为”和“潜伏学习”的概念
▶
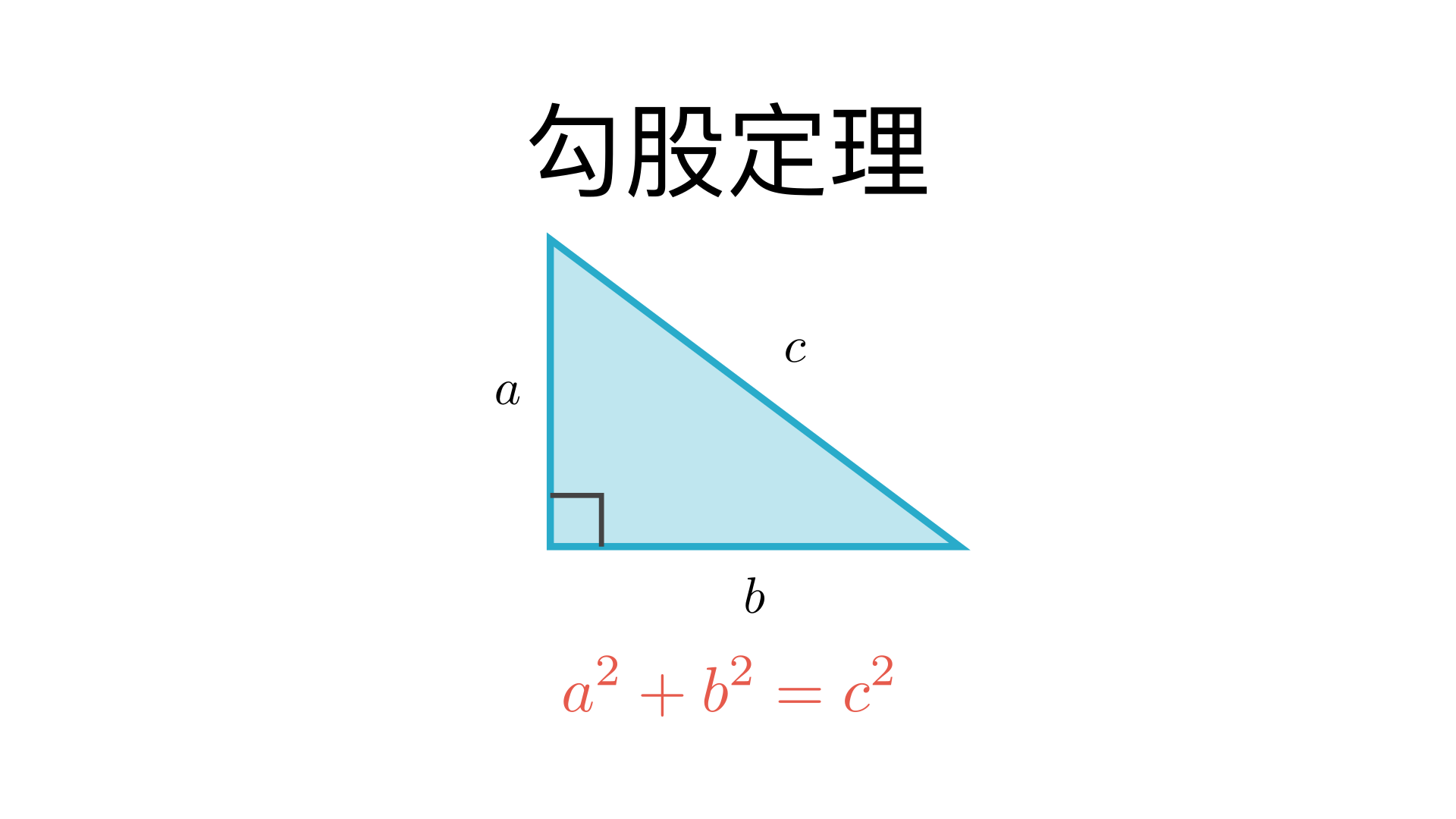
讲解一下勾股定理

▶
Rectangle: area and perimeter
▶
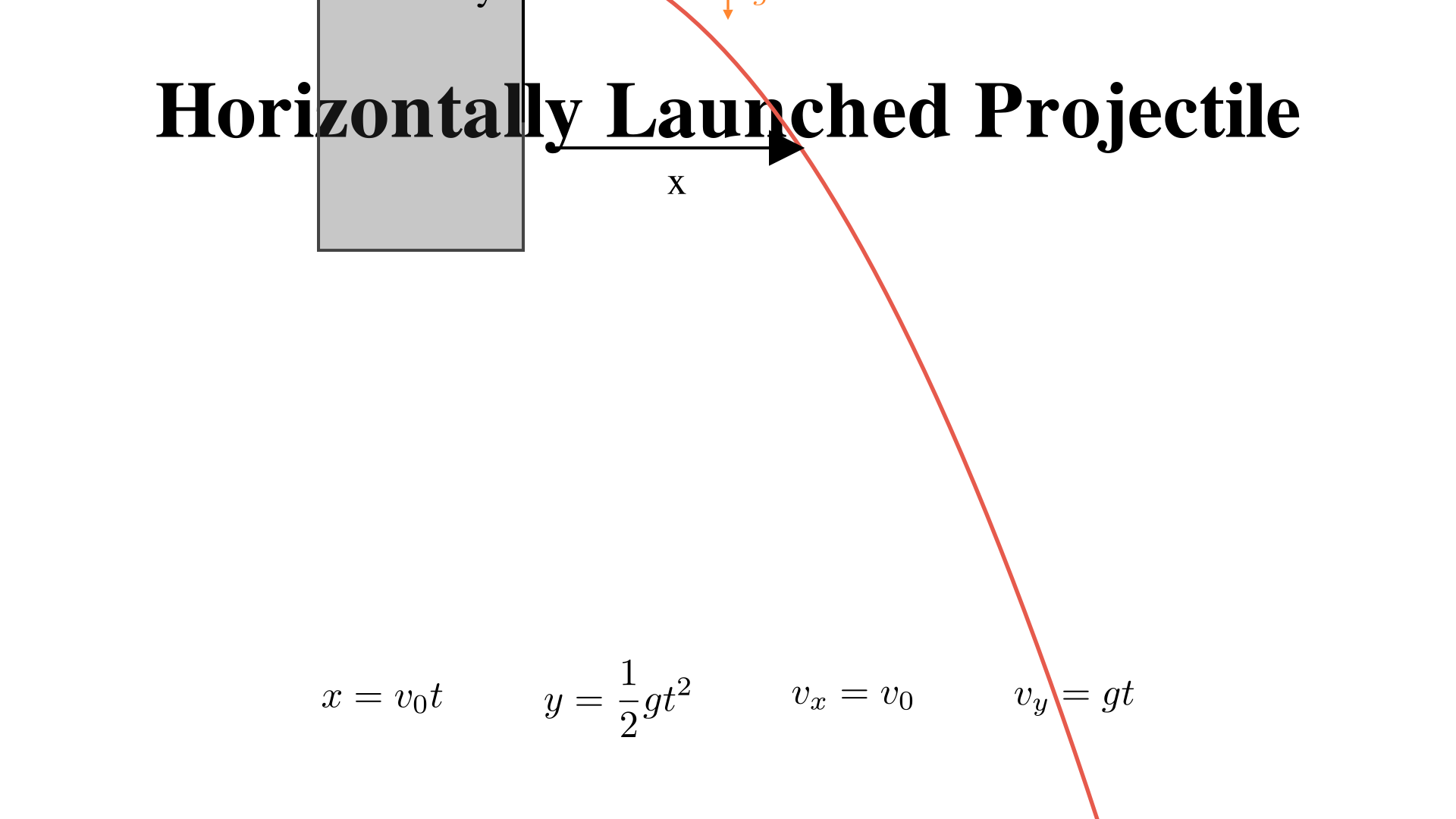
horizontally launched projectile
▶
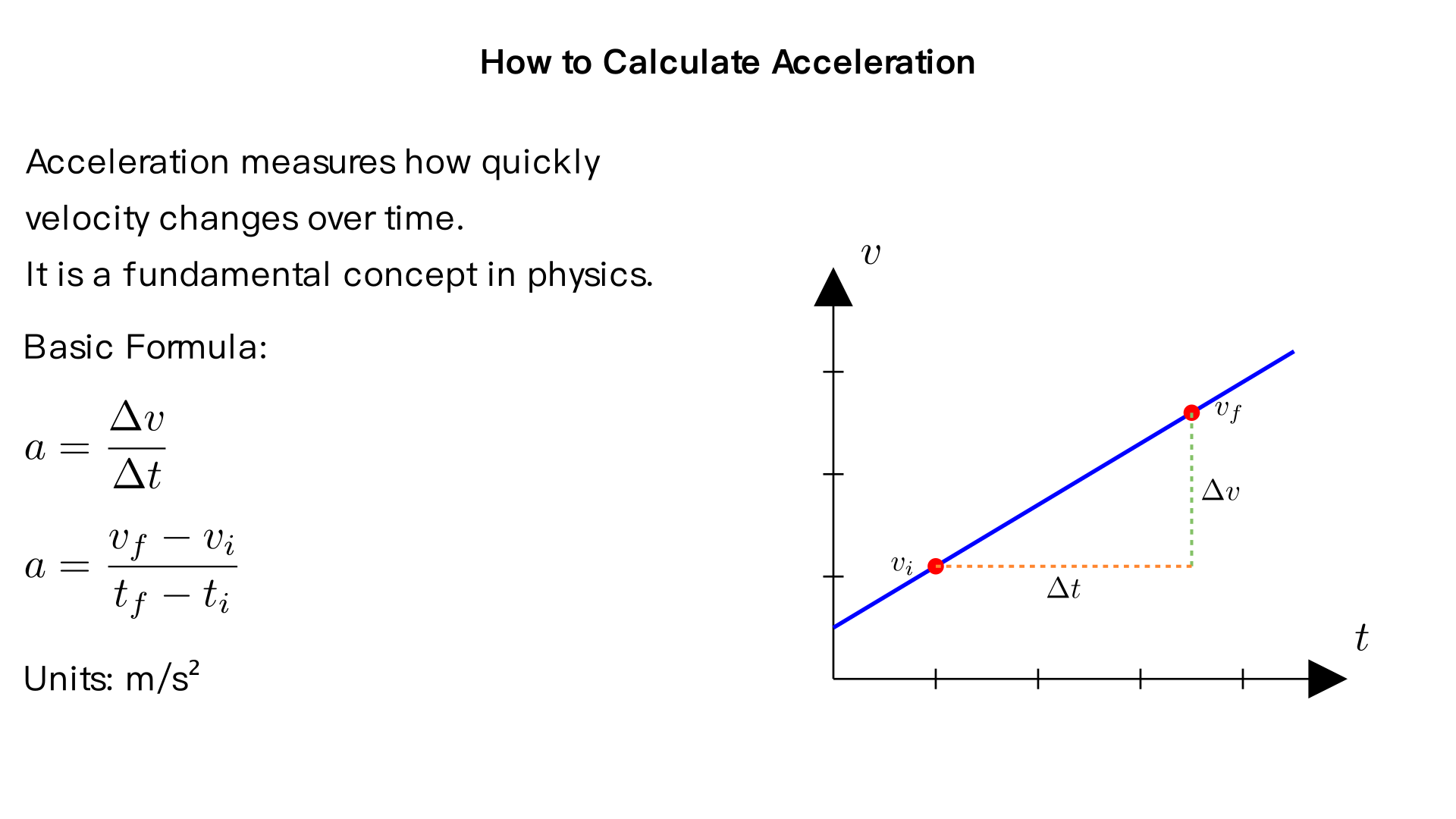
how to calculate acceleration
▶
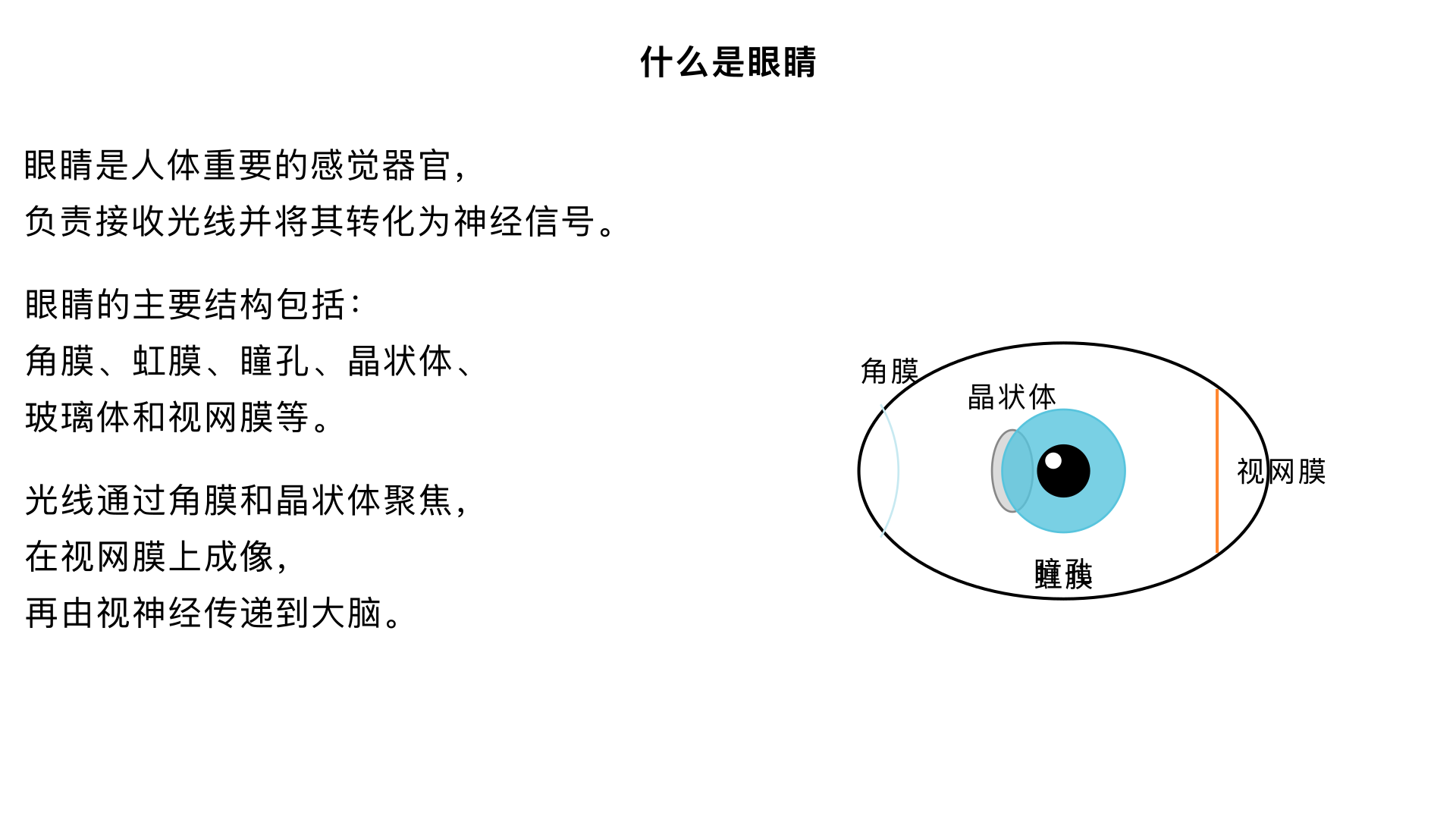
什么是眼睛
▶
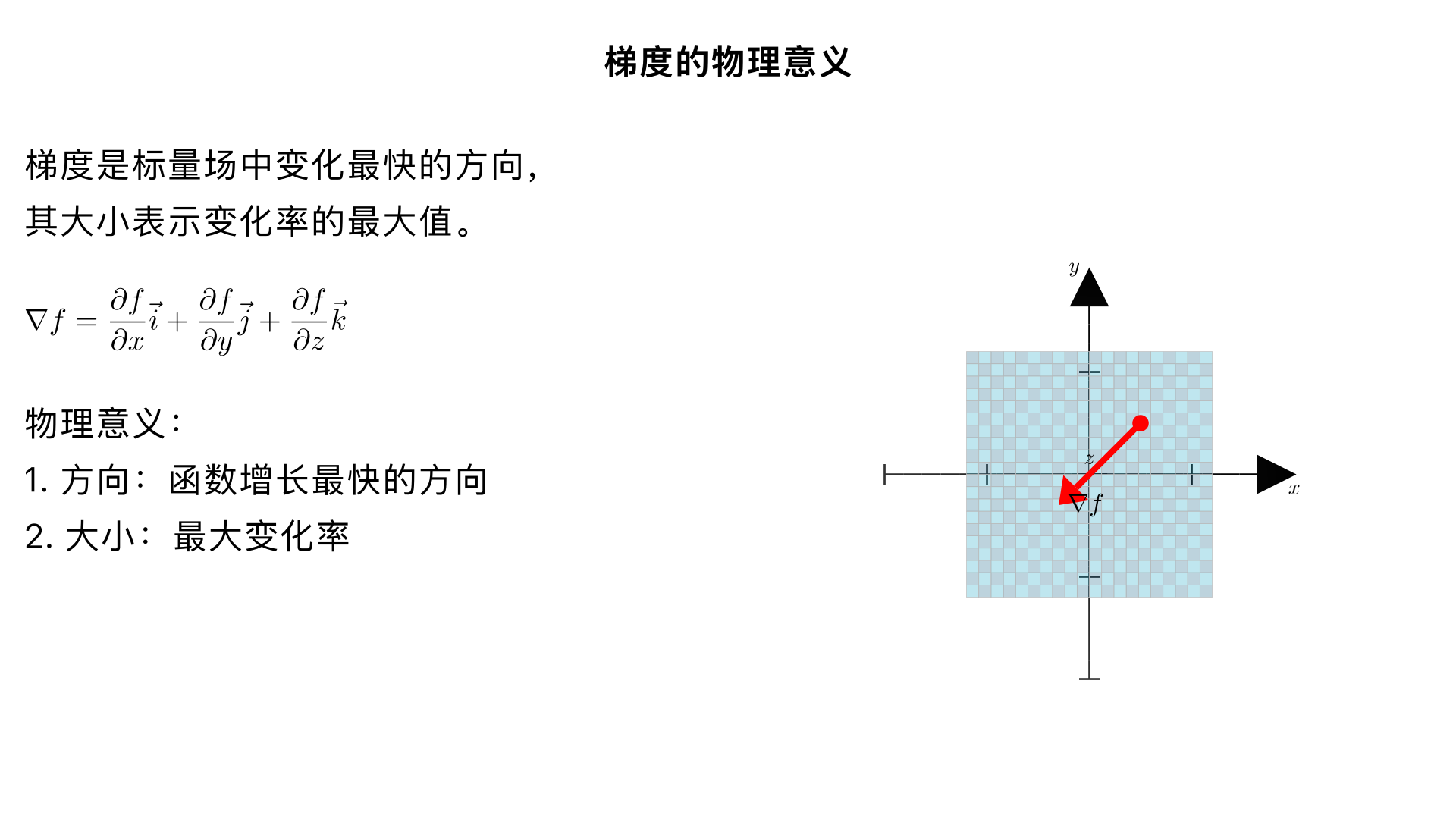
梯度的物理意义是什么?
▶
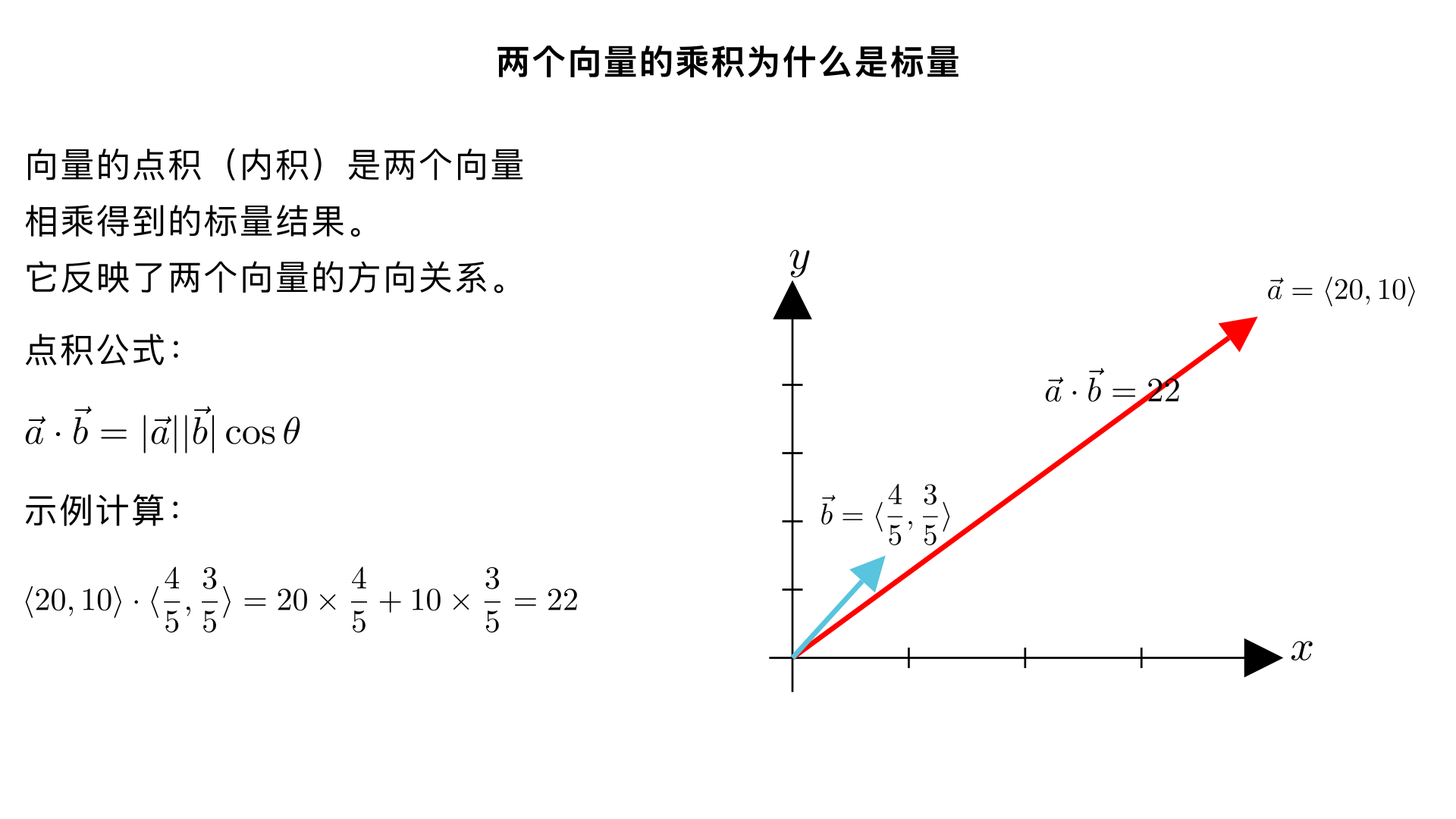
两个向量的乘积为什么是标量 <20,10>x(4/5,3/5>=22

▶