T
Teach Me AnythingTMA
Video History
Page 30 / 44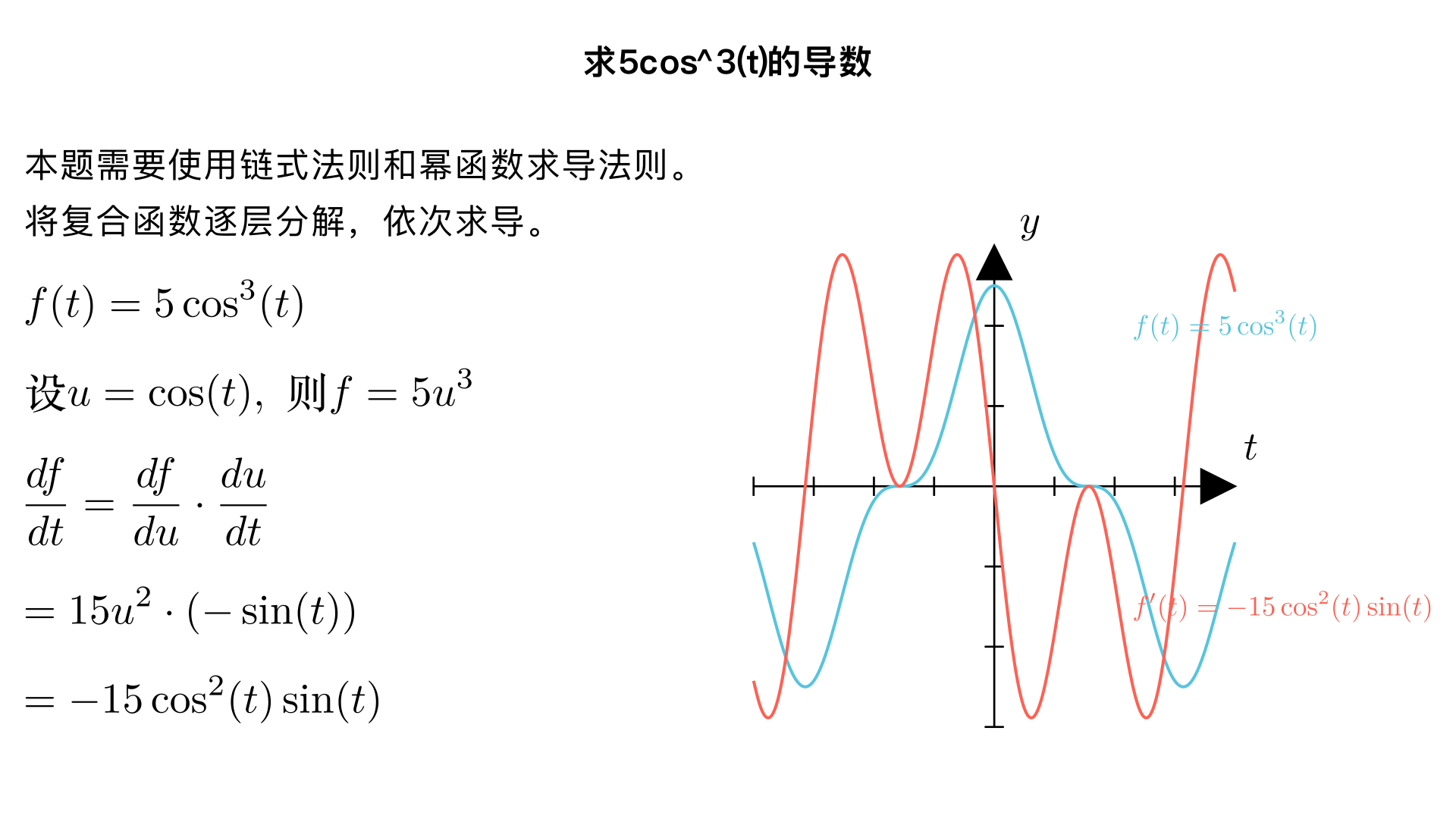
▶
求5cos^3(t)的导数

▶
主题:占卜的后续步骤——变卦与解卦 主要内容: 如何根据三个数字确定“本卦”、“互卦”和“变卦”。 确定“动爻”(变爻)的位置。 解卦的核心:以本卦的卦辞和变爻的爻辞为主,互卦和变卦为辅。

▶
7、梦是愿望的实现吗? (弗洛伊德的“梦的解析”) 主要内容:弗洛伊德提出,梦是通往潜意识的捷径,其内容(显性梦境)是对被压抑的欲望(隐性梦境)的象征性满足。虽然其科学性常受质疑,但该理论对心理学和文化产生了不可估量的影响。
![Find the indicated limit by using the limits
\[
\lim_{(x,y)\to(a,b)} f(x,y) = 5 \quad \text{and} \quad
\lim_{(x,y)\to(a,b)} g(x,y) = -4.
\]
\[
\lim_{(x,y)\to(a,b)} [f(x,y) - g(x,y)]
\]
**Answer:** 9
1.解题 2.讲题 3.使用 MathTex 显示中文](https://manimvideo.explanation.fun/video/cover/578839233902342145.png)
▶
Find the indicated limit by using the limits \[ \lim_{(x,y)\to(a,b)} f(x,y) = 5 \quad \text{and} \quad \lim_{(x,y)\to(a,b)} g(x,y) = -4. \] \[ \lim_{(x,y)\to(a,b)} [f(x,y) - g(x,y)] \] **Answer:** 9 1.解题 2.讲题 3.使用 MathTex 显示中文
![Find the limit (if it exists). (If an answer does not exist, enter DNE.)
\[
\lim_{(x,y)\to(0,0)} \frac{x + y}{x^7 + y}
\]
**Answer:** DNE
1.讲题 2.解题 3.使用 MathTex 显示公式](https://manimvideo.explanation.fun/video/cover/578838266972663809.png)
▶
Find the limit (if it exists). (If an answer does not exist, enter DNE.) \[ \lim_{(x,y)\to(0,0)} \frac{x + y}{x^7 + y} \] **Answer:** DNE 1.讲题 2.解题 3.使用 MathTex 显示公式
▶
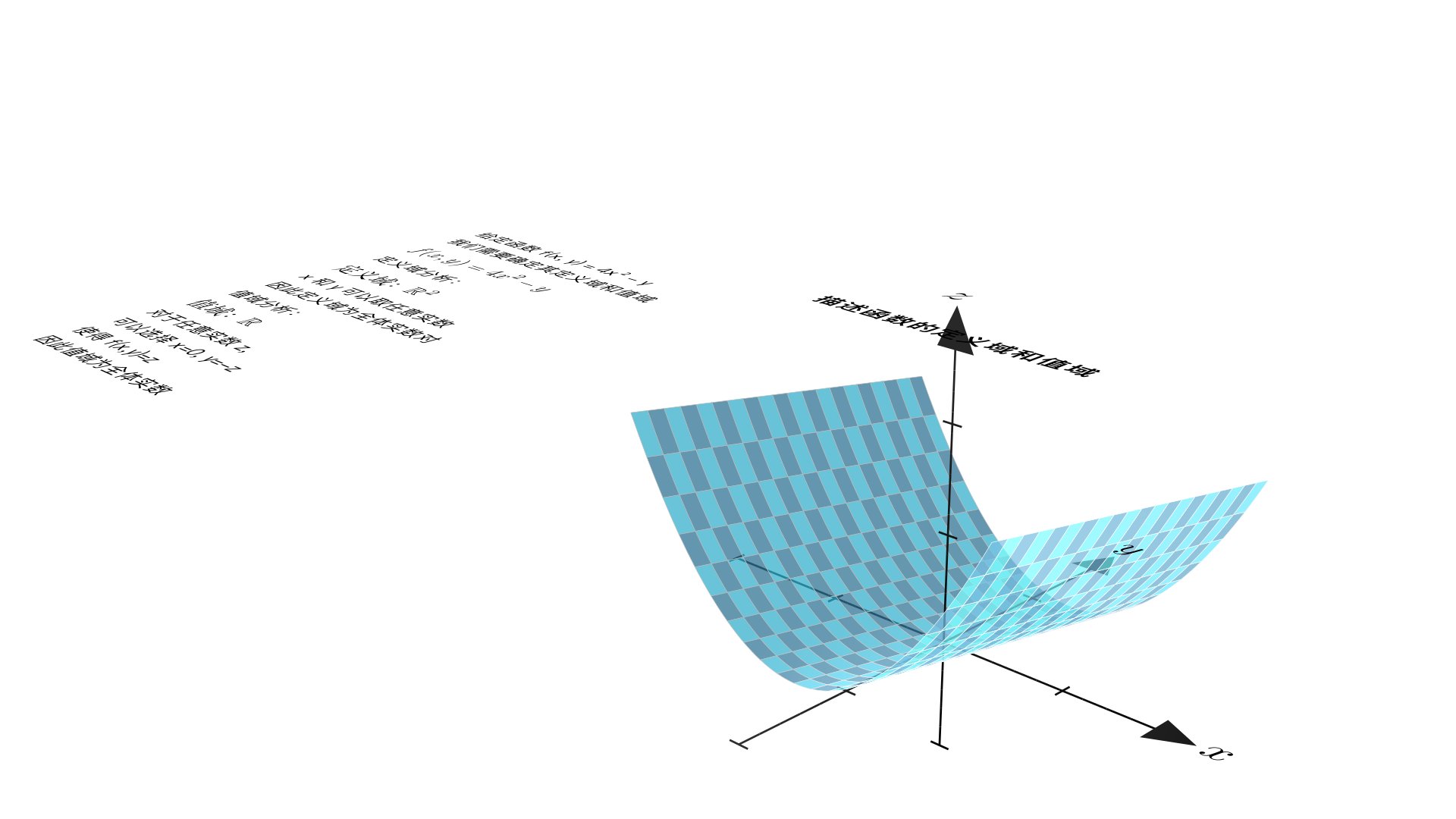
Describe the domain and range of the function. f(x, y) = 4x^2 − y 1.讲题 2.解题 3.使用 MathTex 显示公式
▶
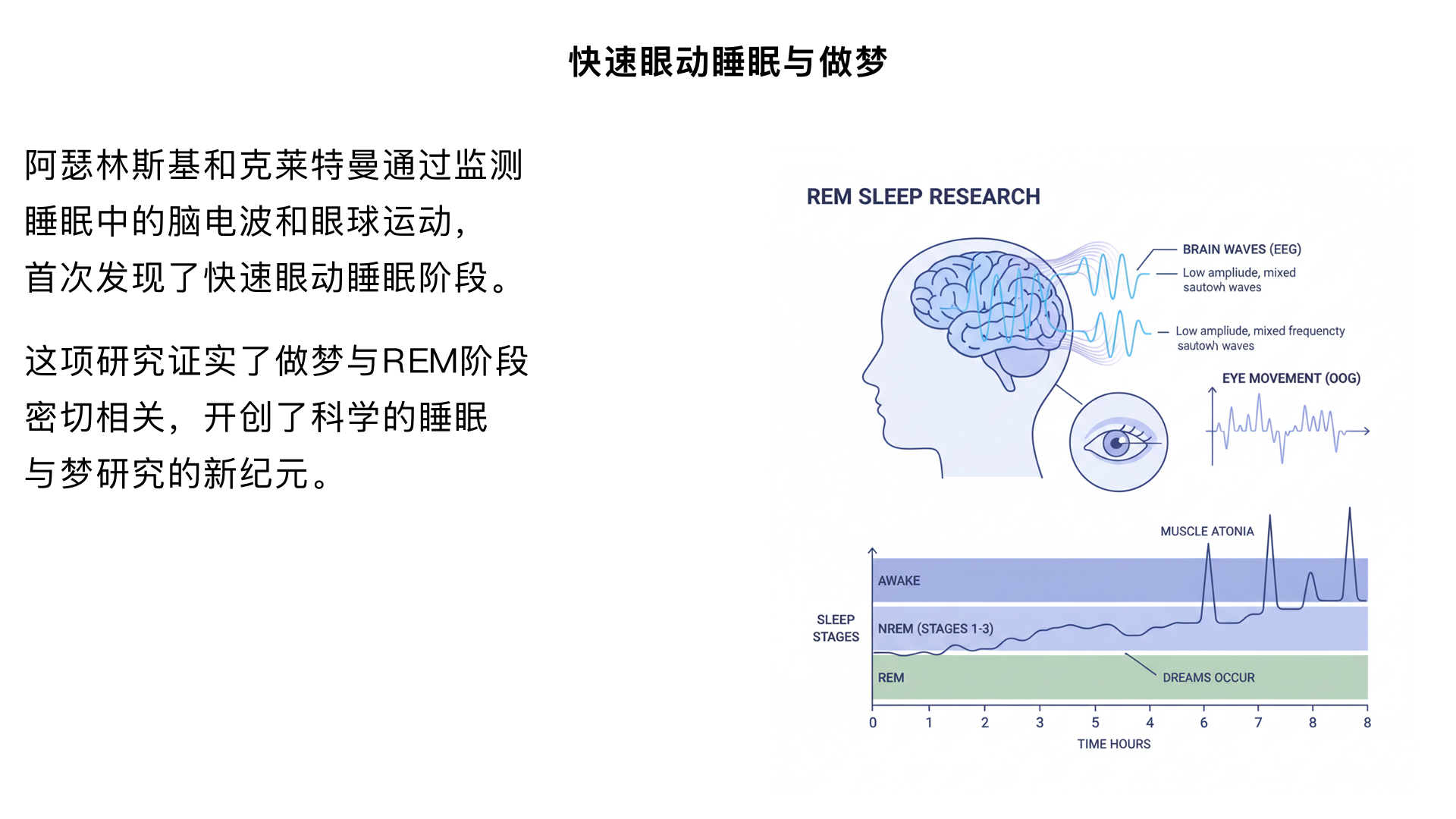
6、睡眠,毫无疑问就会做梦 (阿瑟林斯基和克莱特曼的“快速眼动睡眠”研究) 主要内容:通过监测睡眠中的脑电波和眼球运动,首次发现了快速眼动睡眠阶段,并证实了做梦与此阶段密切相关。这项研究开创了科学的睡眠与梦研究的新纪元。
▶
什么是偏导数
▶
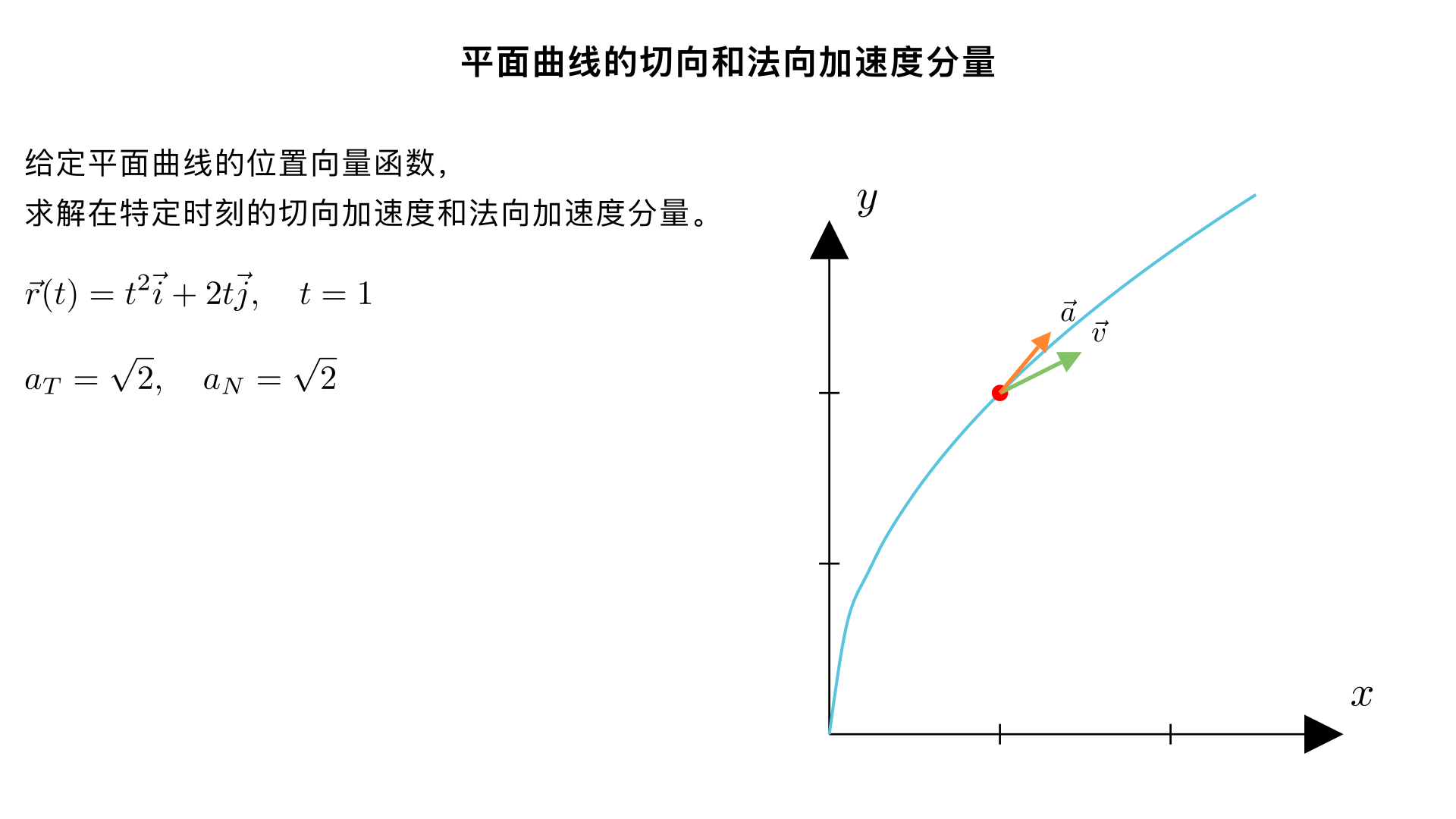
Find the tangential and normal components of acceleration at the given time t for the plane curve **r(t)**. **r(t) = t² i + 2t j, t = 1** \( a_T = \sqrt{2} \) \( a_N = \sqrt{2} \) 1.讲题 2.解题 3.使用 MathTex 显示公式
![**Find the limit (if it exists). (If an answer does not exist, enter DNE.)**
[
\lim_{t \to 0} \left( e^{4t},\mathbf{i} + \frac{\sin(5t)}{5t},\mathbf{j} + e^{-8t},\mathbf{k} \right)
]
**Answer:**
[
\mathbf{i} + \mathbf{j} + \mathbf{k}
]
讲题 解题 使用 Mathtex 显示公式](https://manimvideo.explanation.fun/video/cover/578817939683647489.png)
▶
**Find the limit (if it exists). (If an answer does not exist, enter DNE.)** [ \lim_{t \to 0} \left( e^{4t},\mathbf{i} + \frac{\sin(5t)}{5t},\mathbf{j} + e^{-8t},\mathbf{k} \right) ] **Answer:** [ \mathbf{i} + \mathbf{j} + \mathbf{k} ] 讲题 解题 使用 Mathtex 显示公式
▶
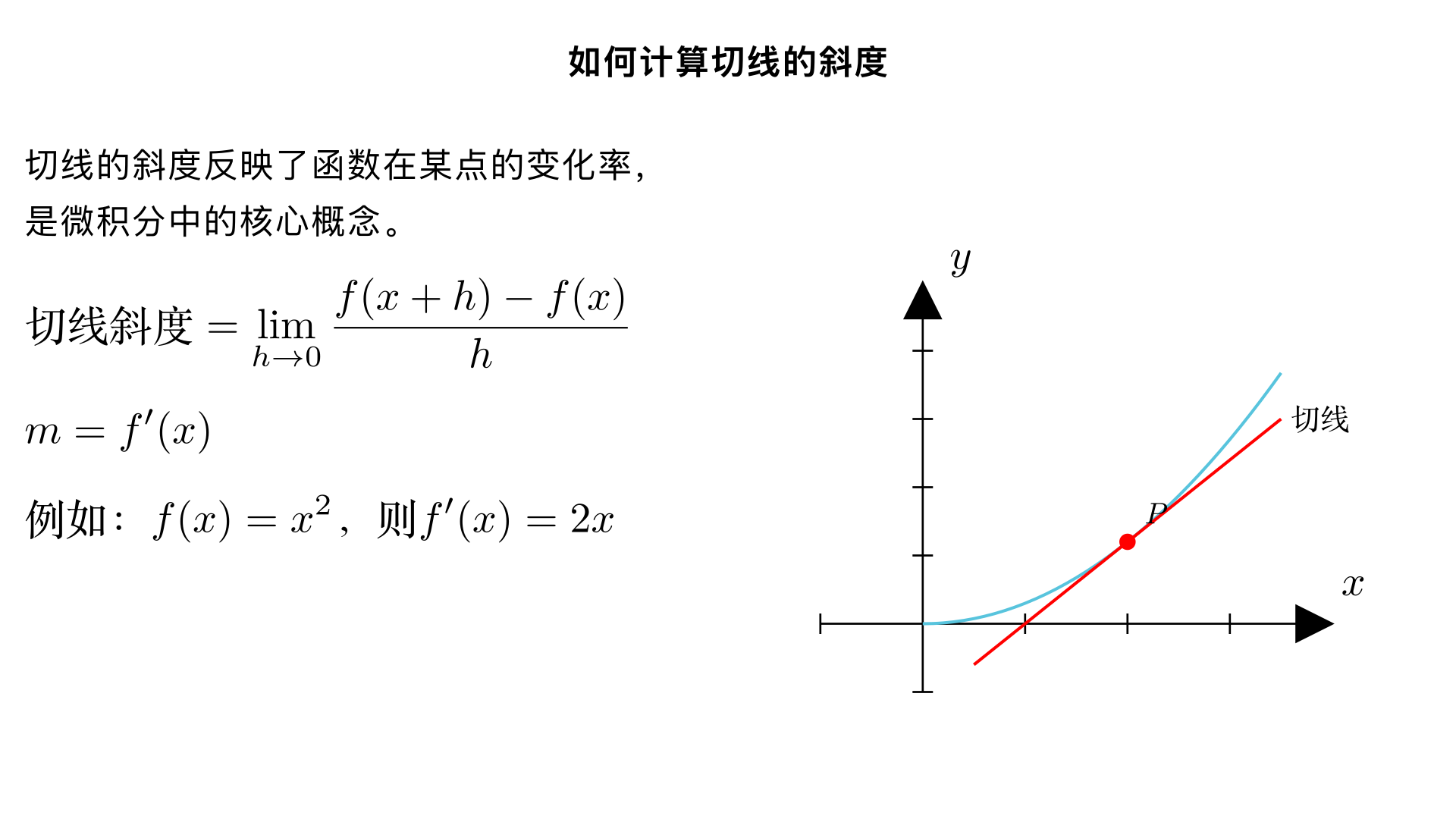
如何计算切线的斜度
![Find the indefinite integral. (Use **c** for the constant of integration.)
\[
\int (2t\,\mathbf{i} + \mathbf{j} + 5\mathbf{k}) \, dt
\]
1.讲题 2.解题](https://manimvideo.explanation.fun/video/cover/578772319945928705.png)
▶