T
Teach Me AnythingTMA
Video History
Page 41 / 44
▶
name:第七部分:综合实例:验证乘法程序 scene1 title:一个更复杂的例子:乘法程序 scene1 content:现在,我们将运用之前学到的所有知识,来验证一个计算两个整数乘积的程序。这个程序包含了条件判断和循环,是一个很好的综合练习。 scene2 title:验证策略:分段与组合 scene2 content:我们的策略是将整个程序分解为四个逻辑片段S1, S2, S3, S4。然后,我们逐一证明每个片段的正确性,最后使用组合规则将它们串联起来,证明整个程序的正确性。 scene3 title:验证S1:处理负数 scene3 content:第一段S1是一个if-else语句,它计算n的绝对值并存入变量a。我们可以证明,在S1执行后,断言 q: 'a = |n|' 成立。这与我们之前验证if-then-else的例子类似。 scene4 title:验证S2:初始化 scene4 content:第二段S2是初始化语句,k:=0, x:=0。在S2执行后,我们可以得到新的断言 r: 'q ∧ (k=0) ∧ (x=0)' 成立。 scene5 title:验证S3:核心循环 scene5 content:第三段S3是while循环。我们需要找到它的循环不变量。这里的循环不变量是 v: 'x = m*k ∧ k ≤ a'。我们需要证明v确实是不变量,并且循环会终止。 scene6 title:证明S3的循环不变量和终止性 scene6 content:首先,在循环开始前,k=0, x=0,满足x=m*k。其次,在循环体内,x增加m,k增加1,不变量关系'x=m*k'得以维持。最后,因为k从0开始每次加1,它最终会等于a,导致循环终止。 scene7 title:S3循环结束后的状态 scene7 content:根据迭代规则,当循环结束时,循环条件k<a为假,且不变量v为真。这意味着 k=a 且 x=m*k,所以我们得到 x = m*a。结合之前的a=|n|,我们得到 x = m*|n|。 scene8 title:验证S4:最终结果调整 scene8 content:第四段S4根据n的符号来确定最终结果。如果n<0,product=-x;否则product=x。我们可以证明,无论哪种情况,最终的product都等于m*n。 scene9 title:最终结论:组合所有证明 scene9 content:我们已经证明了从p{S1}q, q{S2}r, r{S3}s, 到s{S4}t的每一步都是正确的。根据组合规则,我们可以得出最终结论 p{S}t,即整个程序对于任意整数输入m和n,都能正确计算出它们的乘积m*n。课程到此结束,谢谢大家!

▶
name:第六部分:使用循环不变量验证循环 scene1 title:验证循环的挑战 scene1 content:验证带有循环的程序,比如 'while condition do S',是程序验证中最具挑战性的部分,因为我们不知道循环会执行多少次。 scene2 title:循环不变量 (Loop Invariant) scene2 content:为了解决这个问题,我们引入了“循环不变量”的概念。循环不变量是一个断言p,它在循环的每一次迭代之前和之后都保持为真。形式化地,如果(p ∧ condition){S}p成立,那么p就是一个循环不变量。 scene3 title:迭代规则 (Rule of Iteration) scene3 content:基于循环不变量,我们有了迭代规则:如果p是一个循环不变量,那么我们可以推断出 p{while condition S}(¬condition ∧ p)。这意味着,如果循环开始前p为真,那么当循环结束时(此时condition为假),p仍然为真。 scene4 title:实例:阶乘程序 scene4 content:我们来验证一个计算n的阶乘的程序。程序中有一个while循环,条件是 i < n。我们需要找到一个循环不变量来证明程序最终能得到 fact = n!。 scene5 title:寻找循环不变量 scene5 content:对于阶乘程序,一个合适的循环不变量p是 '(fact = i!) ∧ (i ≤ n)'。这个断言包含了我们想追踪的状态(fact和i的关系)以及循环能够最终终止的条件。 scene6 title:证明p是循环不变量 scene6 content:我们需要证明在循环体执行前后,p都保持为真。假设在某次循环开始时,p和循环条件i<n都为真。循环体内,i变成i+1,fact变成fact*(i+1)。根据假设,新fact等于(i+1)!,新i小于等于n。所以p在循环体执行后仍然为真。 scene7 title:使用迭代规则证明正确性 scene7 content:证明分为三步:1. 证明循环开始前,p为真。在程序初始化后,i=1, fact=1,此时p成立。2. 应用迭代规则,当循环结束时,i<n为假且p为真。这意味着i=n且fact=i!,即fact=n!。3. 证明循环会终止。因为i每次循环都加1,它最终会达到n,使得循环条件为假,从而终止循环。

▶
name:第五部分:程序验证的推理规则 scene1 title:程序验证的过程 scene1 content:程序验证通常有四个步骤:1. 明确初始和最终断言p和q。2. 将程序分解成小的片段。3. 使用推理规则证明每个片段的正确性。4. 组合起来,证明整个程序的正确性。 scene2 title:组合规则 (Composition Rule) scene2 content:对于顺序执行的两个程序段S1和S2,我们可以使用组合规则。如果我们已经证明了p{S1}q和q{S2}r,那么我们可以推断出p{S1; S2}r。也就是说,S1的后置条件q成为了S2的前置条件。 scene3 title:验证条件语句:if-then scene3 content:如何验证一个 'if condition then S' 形式的语句?我们需要证明两种情况:1. 当p和condition都为真时,执行S后,q为真。2. 当p为真但condition为假时,S不执行,此时q仍然为真。 scene4 title:if-then 推理规则 scene4 content:这两种情况可以形式化为一条推理规则:如果 (p ∧ condition){S}q 和 (p ∧ ¬condition) → q 都成立,那么我们就可以得出结论 p{if condition then S}q 成立。 scene5 title:if-then 规则示例 scene5 content:我们来验证 'if x > y then y := x'。后置条件是 y ≥ x。情况一:如果x > y为真,程序执行y:=x,执行后y=x,所以y≥x成立。情况二:如果x > y为假,即x≤y,程序不执行,y的值不变,此时y≥x也成立。因此,该语句是正确的。 scene6 title:验证条件语句:if-then-else scene6 content:对于 'if condition then S1 else S2' 语句,我们需要证明:1. 当p和condition为真时,执行S1后q为真。2. 当p为真且condition为假时,执行S2后q为真。 scene7 title:if-then-else 推理规则 scene7 content:其形式化的推理规则是:如果 (p ∧ condition){S1}q 和 (p ∧ ¬condition){S2}q 都成立,那么我们就可以得出结论 p{if condition then S1 else S2}q 成立。 scene8 title:if-then-else 规则示例:绝对值 scene8 content:我们来验证一个计算绝对值的程序。如果x<0,abs:=-x;否则,abs:=x。后置条件是abs=|x|。当x<0时,abs被赋值为-x,根据定义这就是|x|。当x≥0时,abs被赋值为x,根据定义这也是|x|。两种情况都满足后置条件,因此程序正确。

▶
name:第四部分:程序验证入门 scene1 title:什么是程序验证? scene1 content:程序验证是软件工程中的一个重要环节,它的目标是证明一个程序是否能完成其预定任务。这不仅仅是运行几次测试,而是通过形式化的方法来证明其正确性。 scene2 title:程序的质量问题 scene2 content:一个高质量的程序不仅要功能正确,还需要考虑效率、代码风格、可读性和易于修改等问题。程序验证主要关注的是“功能正确性”这一核心问题。 scene3 title:部分正确性 vs. 完全正确性 scene3 content:程序正确性分为两种:部分正确性(Partial Correctness)和完全正确性(Total Correctness)。部分正确性指的是:如果程序能够停止运行,那么它产生的结果一定是正确的。而完全正确性则更进一步,它要求程序不仅结果正确,而且必须保证总能停止运行。 scene4 title:断言:前置条件与后置条件 scene4 content:为了进行程序验证,我们引入“断言”的概念。初始断言(Initial Assertion),也叫前置条件(precondition),规定了程序输入需要满足的属性。最终断言(Final Assertion),也叫后置条件(postcondition),规定了程序输出应该满足的属性。 scene5 title:断言的实际应用:JUnit scene5 content:在实际编程中,单元测试框架如JUnit就广泛使用了断言。测试代码中的`Assert.assertTrue`就是一个最终断言,它用来验证程序的输出是否符合预期的属性。 scene6 title:形式化表示:霍尔三元组 (Hoare Triple) scene6 content:部分正确性可以用一种称为“霍尔三元组”的表示法来形式化,记作 p{S}q。它的意思是:如果在执行程序S之前,前置条件p为真,并且程序S能够终止,那么在S执行完毕后,后置条件q必然为真。 scene7 title:一个简单的部分正确性证明 scene7 content:来看一个例子:程序段 y:=2; z:=x+y。前置条件p是x=1,后置条件q是z=3。假设p为真,即x=1。程序执行第一步后y=2。执行第二步后z=x+y=1+2=3。此时后置条件q为真。因此,该程序段关于给定的p和q是部分正确的。
▶
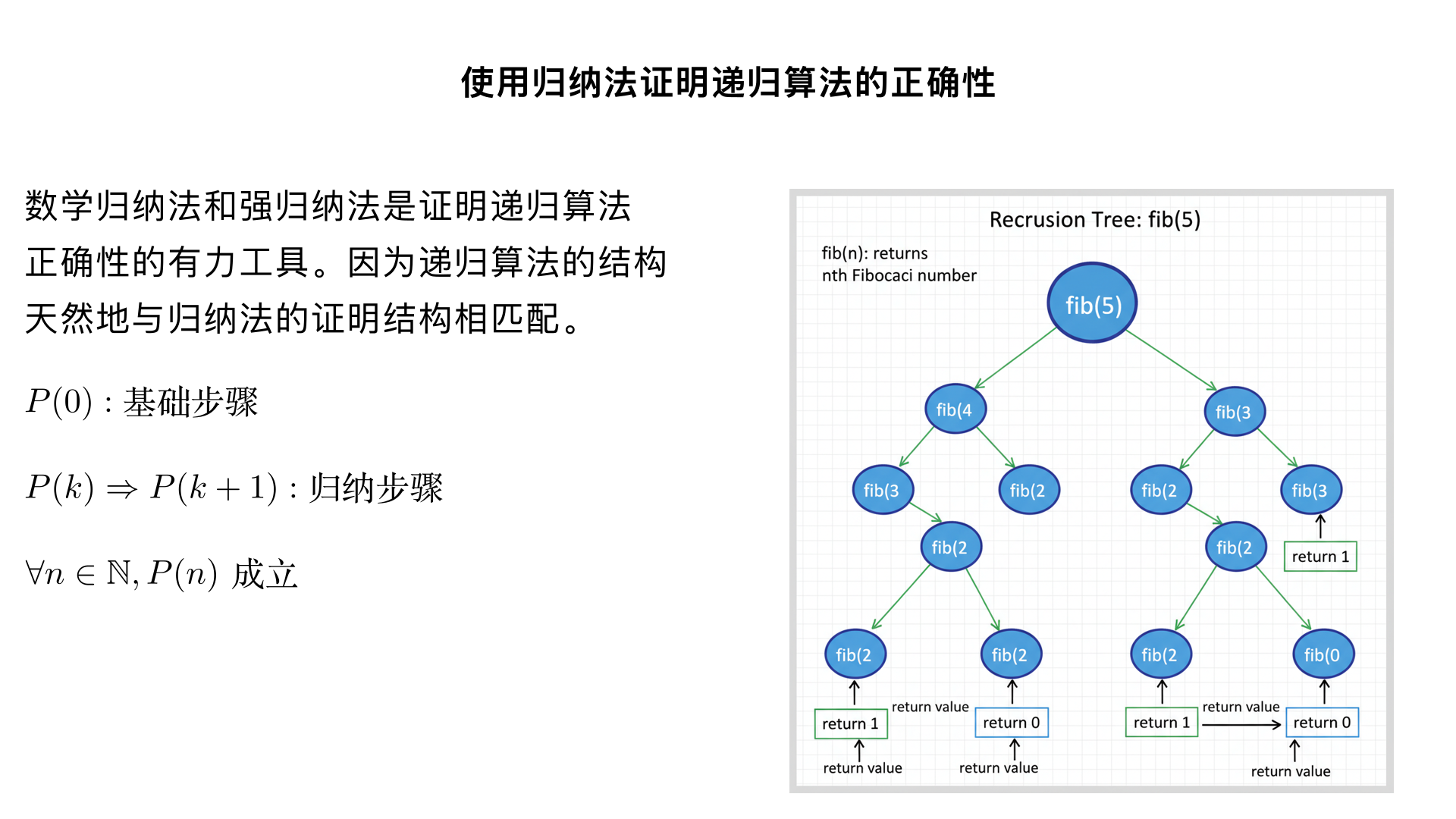
name:第三部分:使用归纳法证明递归算法的正确性 scene1 title:归纳法与递归算法 scene1 content:数学归纳法和强归纳法是证明递归算法正确性的有力工具。因为递归算法的结构天然地与归纳法的证明结构相匹配。 scene2 title:实例:计算幂的递归算法 scene2 content:我们来看一个计算a的n次幂的递归算法。当n=0时,返回1;否则,返回a乘以power(a, n-1)的结果。我们要证明这个算法对于所有非负整数n都能正确计算出a的n次方。 scene3 title:建立证明框架 scene3 content:我们使用对指数n的归纳法来证明。设P(n)为命题:函数power(a, n)能正确返回a的n次方。 scene4 title:基础步骤:证明P(0) scene4 content:基础步骤是证明P(0)为真。根据算法定义,当n=0时,函数直接返回1。而任何非零实数a的0次方都等于1。因此,P(0)成立。 scene5 title:归纳步骤:归纳假设P(k) scene5 content:我们的归纳假设是:对于某个非负整数k,P(k)为真。也就是说,我们假设power(a, k)能够正确地返回a的k次方。 scene6 title:归纳步骤:证明P(k+1) scene6 content:现在我们需要证明P(k+1)也为真。根据算法,power(a, k+1)会返回 a * power(a, k)。根据我们的归纳假设,power(a, k)的结果是a的k次方。所以,整个表达式的结果是 a * a^k,也就是a^(k+1)。 scene7 title:结论 scene7 content:我们已经证明了基础步骤和归纳步骤都成立。因此,通过数学归纳法,我们得出结论:这个递归算法对于所有非负整数n和非零实数a,都能正确地计算出a的n次方。
▶
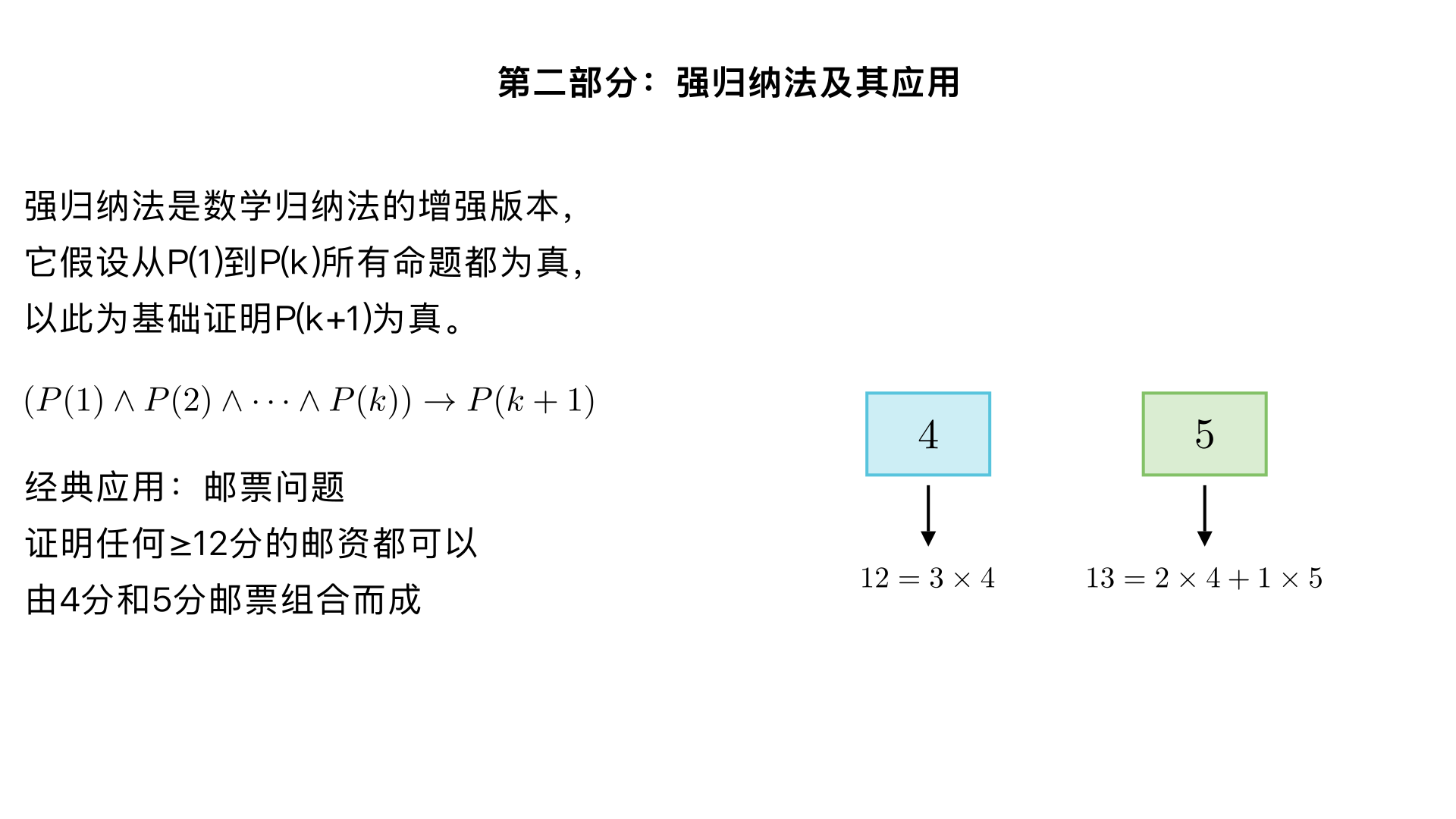
name:第二部分:强归纳法及其应用 scene1 title:什么是强归纳法? scene1 content:现在我们来学习强归纳法。与普通归纳法不同,强归纳法的归纳假设更“强”。它假设从P(1)到P(k)所有的命题都为真,并以此为基础来证明P(k+1)为真。 scene2 title:强归纳法的步骤 scene2 content:强归纳法的步骤包括:基础步骤,这里可能需要验证多个初始情况,比如P(1), P(2)等。然后是归纳步骤,即证明 (P(1) ∧ P(2) ∧ ... ∧ P(k)) → P(k+1) 这个条件语句对于所有正整数k都成立。 scene3 title:应用实例:邮票问题 scene3 content:让我们用一个有趣的例子来理解强归纳法:证明任何大于等于12分的邮资,都可以由4分和5分的邮票组合而成。 scene4 title:定义命题P(n) scene4 content:首先,我们定义命题P(n)为:n分的邮资可以由4分和5分的邮票组合而成。我们的目标是证明对于所有n≥12,P(n)都为真。 scene5 title:基础步骤 (Basis Step) scene5 content:对于这个问题,我们需要验证几个基础情况。例如:P(12)可以通过3张4分邮票实现。P(13)可以通过2张4分和1张5分邮票实现。P(14)是1张4分和2张5分。P(15)是3张5分。这些基础情况都成立。 scene6 title:归纳步骤 (Inductive Step) scene6 content:我们的归纳假设是:对于从12到k的任意整数j,P(j)都为真。现在我们要证明P(k+1)也为真。我们可以考虑k+1分的邮资,减去一张4分的邮票,剩下k-3分。因为我们假设P(k-3)为真,所以k-3分的邮资可以组合出来,那么k+1分的邮资也就可以组合出来了。 scene7 title:强归纳法总结 scene7 content:通过邮票问题的例子,我们可以看到,当证明P(k+1)需要依赖不止P(k)一个前项时,强归纳法就显得非常有用。它为我们提供了更强大的假设基础。
▶
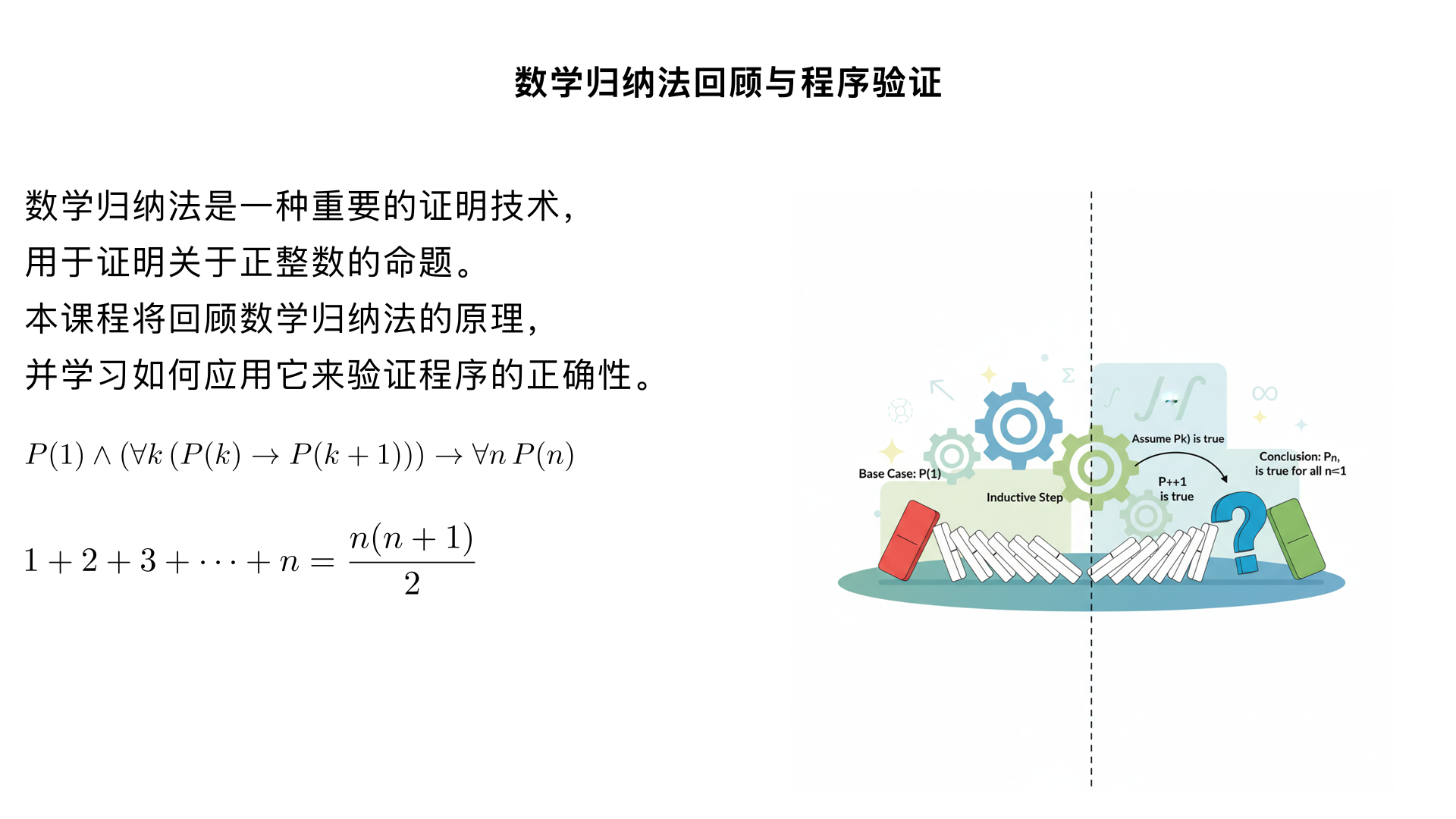
name:第一部分:数学归纳法回顾 scene1:欢迎语与课程介绍 scene1:大家好,欢迎来到ICS 241课程的第14个主题:归纳法回顾与程序验证。本节课我们将回顾数学归纳法,并学习如何应用它来证明程序的正确性。 scene2:什么是数学归纳法? scene2:数学归纳法是一种重要的证明技术。它的核心思想可以表示为一个推理规则:如果我们能证明P(1)为真,并且能证明对于任意的k,如果P(k)为真则P(k+1)也为真,那么我们就可以断定P(n)对于所有正整数n都为真。 scene3:证明实例:前n个正整数的和 scene3:让我们来看一个经典的例子:证明前n个正整数的和等于 n*(n+1)/2。我们将使用数学归纳法来证明这个公式的正确性。 scene4:第一步:基础步骤 (Basis Step) scene4:证明的第一步是基础步骤。我们需要验证当n=1时,命题P(1)是否成立。将n=1代入公式,左边是1,右边是1*(1+1)/2,也等于1。所以,P(1)为真。 scene5:第二步:归纳步骤 (Inductive Step) - 归纳假设 scene5:接下来是归纳步骤。我们首先做出归纳假设:假设对于某个正整数k,命题P(k)是成立的。也就是说,我们假设前k个整数的和确实等于 k*(k+1)/2。 scene6:归纳步骤 - 证明P(k+1) scene6:现在,我们需要在归纳假设的基础上,证明P(k+1)也成立。P(k+1)指的是前k+1个整数的和。我们可以把它写成前k项和,再加上第k+1项。 scene7:代数推导 scene7:根据归纳假设,我们将前k项和替换为k*(k+1)/2。然后通过通分和提取公因式(k+1)进行代数运算,最终得到表达式 (k+1)*(k+2)/2。这正是我们想要证明的P(k+1)的形式。 scene8:结论 scene8:因为我们成功证明了基础步骤和归纳步骤,所以根据数学归纳法原理,我们可以得出结论:对于所有正整数n,前n个正整数的和的公式是成立的。
▶
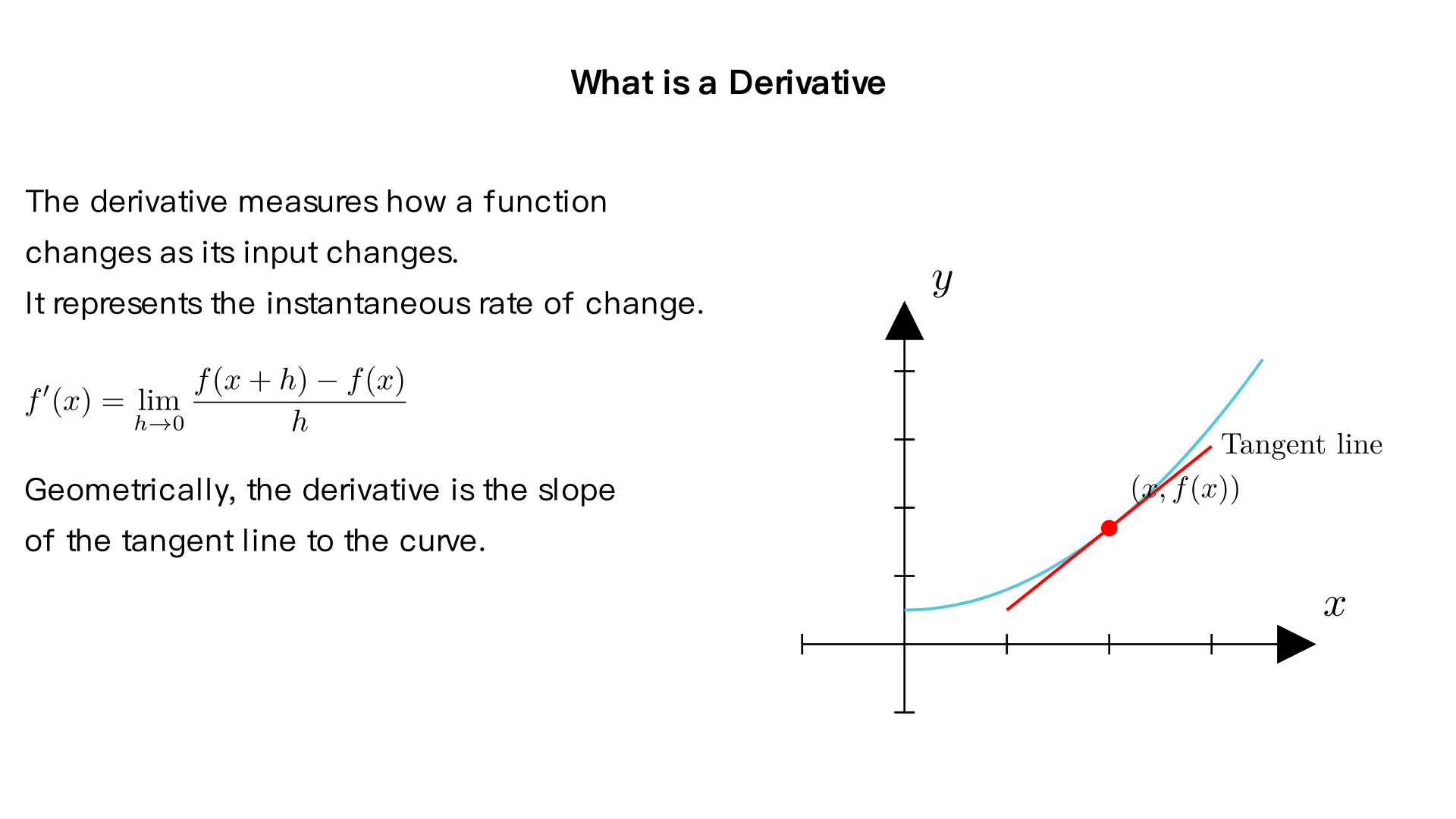
What is a derivative
▶
What is a derivative
▶
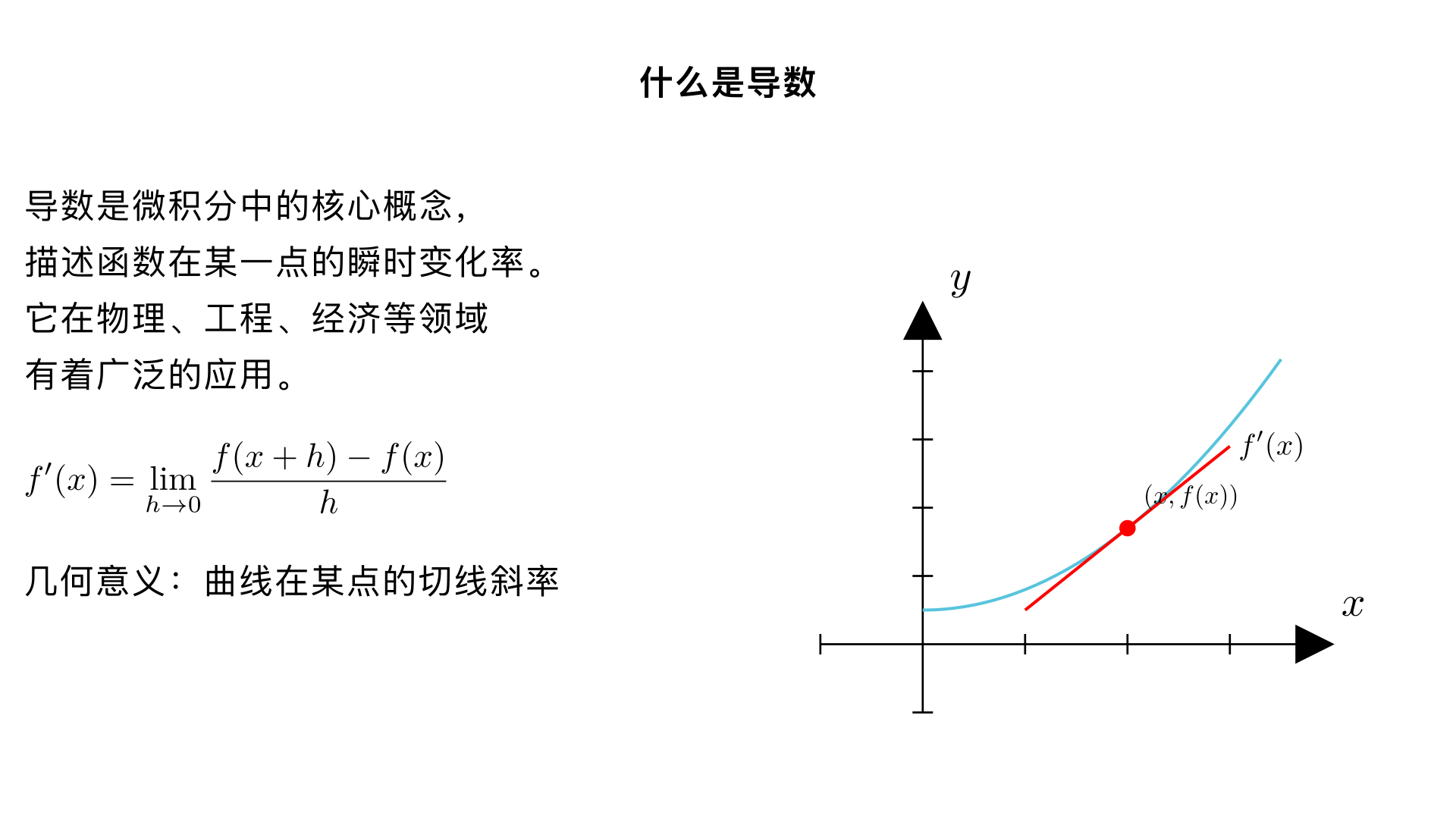
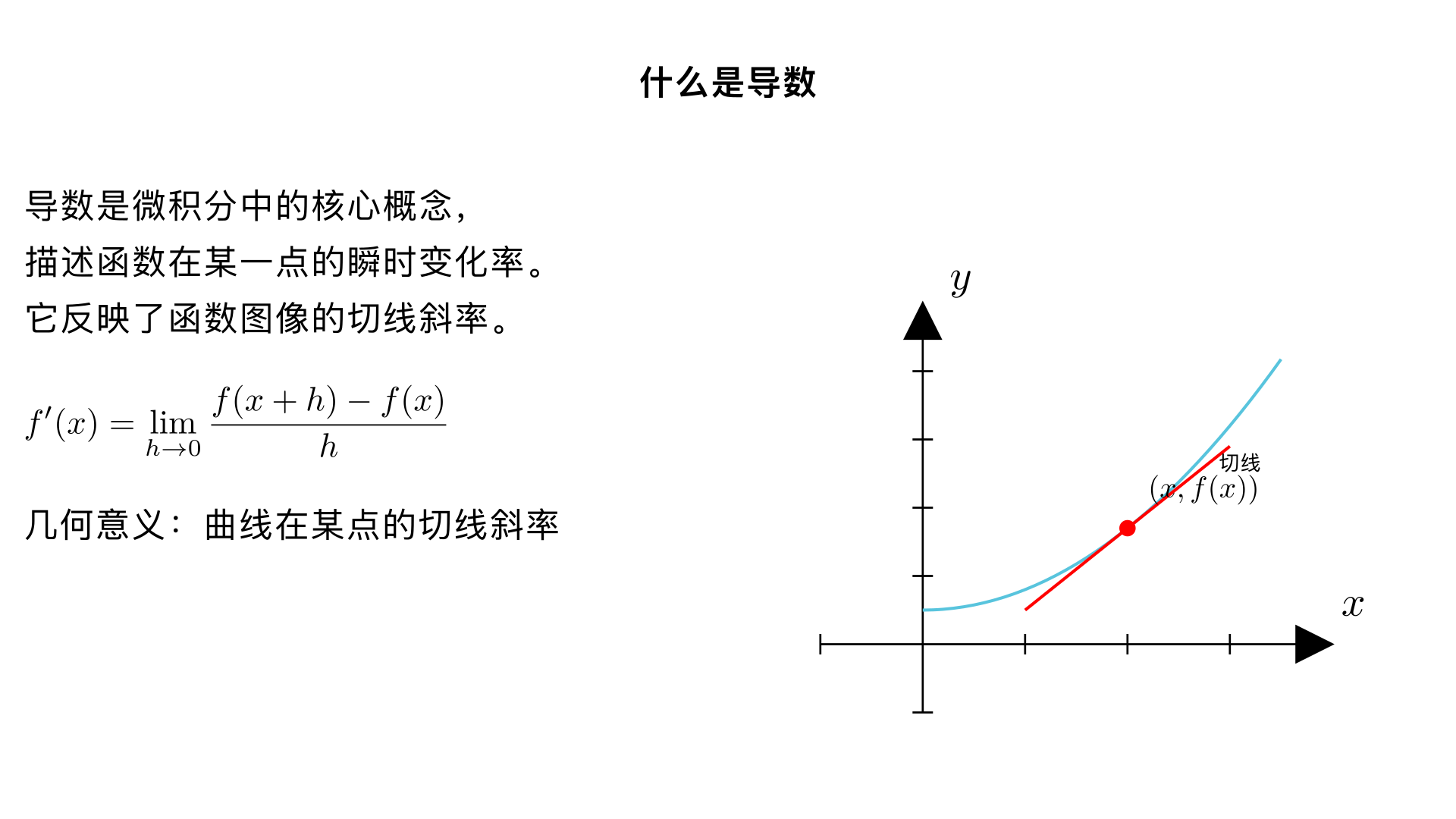
什么是 导数
▶
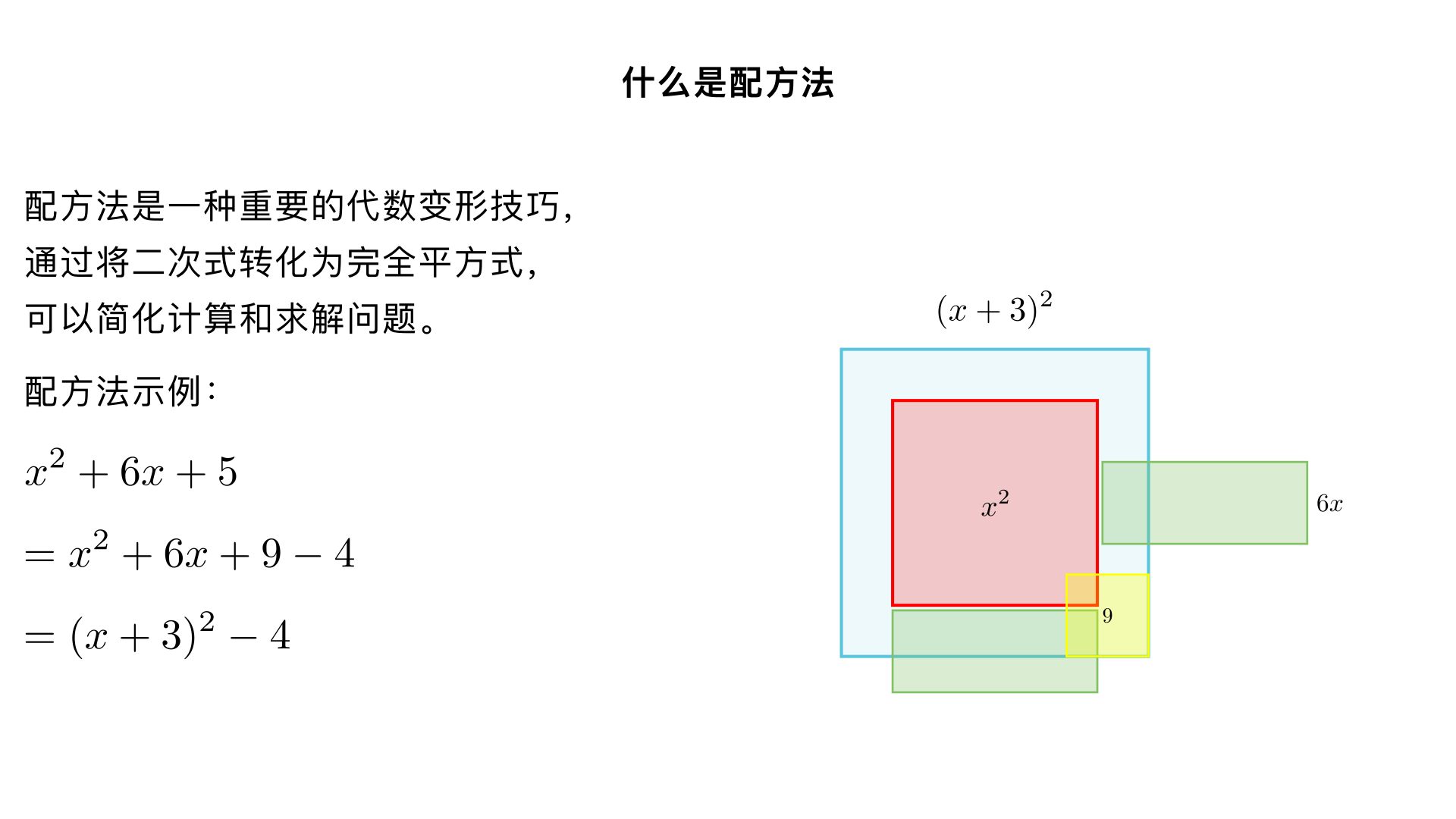
什么是配方法
▶