T
Teach Me AnythingTMA
Video History
Page 8 / 44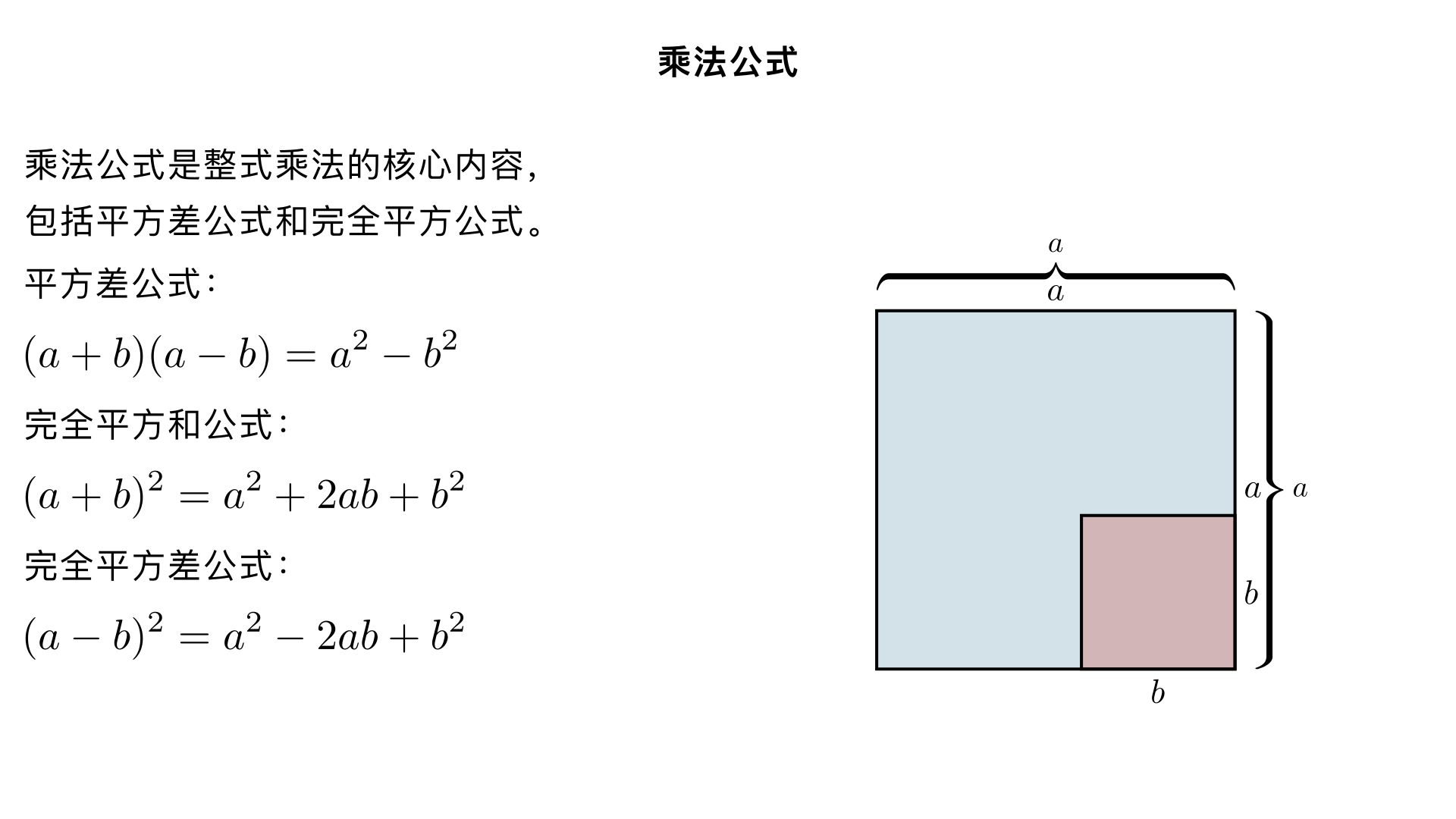
▶
八年级数学 / 整式的乘法 / 乘法公式 乘法公式是整式乘法的核心内容,主要包括平方差公式和完全平方公式,它们是多项式乘法的特殊形式,能大幅简化运算。以下按 “公式 - 推导 - 结构 - 应用 - 题型 - 易错点” 的逻辑系统梳理,方便学习与复习。 一、基础运算回顾(前置知识) 运算类型 公式 语言描述 同底数幂乘法 a m ⋅a n =a m+n 底数不变,指数相加 幂的乘方 (a m ) n =a mn 底数不变,指数相乘 积的乘方 (ab) n =a n b n 积的每个因式分别乘方,再把所得幂相乘 多项式乘法 (a+b)(c+d)=ac+ad+bc+bd 用一个多项式每一项乘另一个多项式每一项,再相加 二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2
![八年级数学 / 整式的乘法 / 乘法公式
乘法公式是整式乘法的核心内容,主要包括平方差公式和完全平方公式,它们是多项式乘法的特殊形式,能大幅简化运算。以下按 “公式 - 推导 - 结构 - 应用 - 题型 - 易错点” 的逻辑系统梳理,方便学习与复习。
一、基础运算回顾(前置知识)
运算类型 公式 语言描述
同底数幂乘法
a
m
⋅a
n
=a
m+n
底数不变,指数相加
幂的乘方
(a
m
)
n
=a
mn
底数不变,指数相乘
积的乘方
(ab)
n
=a
n
b
n
积的每个因式分别乘方,再把所得幂相乘
多项式乘法
(a+b)(c+d)=ac+ad+bc+bd
用一个多项式每一项乘另一个多项式每一项,再相加
二、核心乘法公式详解
1. 平方差公式
标准形式:
(a+b)(a−b)=a
2
−b
2
语言描述:两数和与这两数差的积,等于这两数的平方差
推导过程(多项式乘法展开):
(a+b)(a−b)
=a⋅a+a⋅(−b)+b⋅a+b⋅(−b)
=a
2
−ab+ab−b
2
=a
2
−b
2
结构特点:
左边:两个二项式相乘,其中一项完全相同(
a
),另一项互为相反数(
b
与
−b
)
右边:相同项的平方减去相反项的平方(同方减反方)
几何意义:边长为
a
的正方形中挖去边长为
b
的小正方形,剩余部分面积为
a
2
−b
2
,可拼成一个长
(a+b)
、宽
(a−b)
的矩形
2. 完全平方公式(和与差)
完全平方和公式:
标准形式:
(a+b)
2
=a
2
+2ab+b
2
语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍
完全平方差公式:
标准形式:
(a−b)
2
=a
2
−2ab+b
2
语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍
推导过程(以和为例):
(a+b)
2
=(a+b)(a+b)
=a⋅a+a⋅b+b⋅a+b⋅b
=a
2
+2ab+b
2
结构特点(口诀:首平方,尾平方,积的 2 倍在中央):
左边:二项式的平方(两个相同二项式相乘)
右边:三项式,包含首项平方(
a
2
)、尾项平方(
b
2
)、中间交叉项的 2 倍(
±2ab
),符号与左边二项式中间符号相同
几何意义(以和为例):边长为
a+b
的正方形,可分为边长为
a
的正方形、边长为
b
的正方形,以及两个长
a
宽
b
的矩形,面积和为
a
2
+2ab+b
2
三、公式的灵活应用
1. 基本应用:直接套用公式
平方差公式示例:
(x+3)(x−3)=x
2
−3
2
=x
2
−9
(2a+5b)(2a−5b)=(2a)
2
−(5b)
2
=4a
2
−25b
2
完全平方公式示例:
(m+4)
2
=m
2
+2⋅m⋅4+4
2
=m
2
+8m+16
(3x−2y)
2
=(3x)
2
−2⋅3x⋅2y+(2y)
2
=9x
2
−12xy+4y
2
2. 变形应用:公式的逆用与拓展
公式变形 表达式 应用场景
平方差逆用
a
2
−b
2
=(a+b)(a−b)
因式分解、简便计算
完全平方逆用
a
2
±2ab+b
2
=(a±b)
2
因式分解、配方
完全平方和差关系
(a+b)
2
−(a−b)
2
=4ab
求
ab
值
平方和公式
a
2
+b
2
=(a+b)
2
−2ab=(a−b)
2
+2ab
知和求平方和、知差求平方和
示例:
若
x+y=5
,
xy=3
,求
x
2
+y
2
x
2
+y
2
=(x+y)
2
−2xy=5
2
−2×3=25−6=19
3. 特殊形式应用(换元思想)
当公式中的
a
、
b
为多项式时,可将其视为一个整体套用公式:
(a+b+c)(a+b−c)=[(a+b)+c][(a+b)−c]=(a+b)
2
−c
2
=a
2
+2ab+b
2
−c
2
(x−y+z)
2
=[(x−y)+z]
2
=(x−y)
2
+2(x−y)z+z
2
=x
2
−2xy+y
2
+2xz−2yz+z
2
4. 简便计算应用
利用公式简化复杂计算:
99×101=(100−1)(100+1)=100
2
−1
2
=10000−1=9999
102
2
=(100+2)
2
=100
2
+2×100×2+2
2
=10000+400+4=10404
99
2
=(100−1)
2
=100
2
−2×100×1+1
2
=10000−200+1=9801
四、常见题型分类解析
题型 解题关键 示例
公式直接计算 识别公式结构,找准
a
、
b
(−2m−3n)
2
=(2m+3n)
2
=4m
2
+12mn+9n
2
公式逆用(因式分解) 识别平方差或完全平方式
x
2
−6x+9=(x−3)
2
条件求值 利用公式变形,整体代入 已知
a−b=3
,求
a
2
+b
2
−6ab
(变形为
(a−b)
2
−4ab
)
配方求最值 配成完全平方式,利用平方非负性 求
x
2
−4x+5
最小值(配方为
(x−2)
2
+1
,最小值 1)
化简求值 先化简再代入,避免繁琐计算 化简
(2x+1)
2
−(2x−1)
2
,再代入
x=
4
1
五、易错点警示与避错技巧
易错点 错误示例 正确做法
完全平方漏中间项
(a+b)
2
=a
2
+b
2
牢记 “首平方,尾平方,积的 2 倍在中央”,中间项为
2ab
完全平方符号错误
(a−b)
2
=a
2
−2ab−b
2
尾项平方恒为正,应为
a
2
−2ab+b
2
平方差公式误用
(a+b)(c−d)=a
2
−b
2
必须满足 “一项同,一项反”,不同则用多项式乘法
系数未平方
(2a)
2
=2a
2
系数与字母都要平方,应为
4a
2
符号处理错误
(−a−b)
2
=a
2
−2ab+b
2
提取负号再平方:
(−a−b)
2
=(a+b)
2
=a
2
+2ab+b
2
避错口诀:
平方差:同方减反方,符号要对好
完全平方:和平方加两倍,差平方减两倍,尾项平方永为正
遇负号:先定号,再平方,避免符号乱
六、思维拓展:拓展乘法公式(选学)
三数和平方公式:
(a+b+c)
2
=a
2
+b
2
+c
2
+2ab+2ac+2bc
立方和公式:
(a+b)(a
2
−ab+b
2
)=a
3
+b
3
立方差公式:
(a−b)(a
2
+ab+b
2
)=a
3
−b
3
总结
乘法公式是代数运算的基础工具,核心在于理解公式的结构特征与推导本质,而非死记硬背。通过大量练习掌握直接应用、逆用与变形应用,同时警惕常见易错点,就能熟练运用公式解决各类问题,为后续因式分解、二次函数等学习打下坚实基础。](https://manimvideo.explanation.fun/video/cover/595653712674344960.png)
▶
八年级数学 / 整式的乘法 / 乘法公式 乘法公式是整式乘法的核心内容,主要包括平方差公式和完全平方公式,它们是多项式乘法的特殊形式,能大幅简化运算。以下按 “公式 - 推导 - 结构 - 应用 - 题型 - 易错点” 的逻辑系统梳理,方便学习与复习。 一、基础运算回顾(前置知识) 运算类型 公式 语言描述 同底数幂乘法 a m ⋅a n =a m+n 底数不变,指数相加 幂的乘方 (a m ) n =a mn 底数不变,指数相乘 积的乘方 (ab) n =a n b n 积的每个因式分别乘方,再把所得幂相乘 多项式乘法 (a+b)(c+d)=ac+ad+bc+bd 用一个多项式每一项乘另一个多项式每一项,再相加 二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2 三、公式的灵活应用 1. 基本应用:直接套用公式 平方差公式示例: (x+3)(x−3)=x 2 −3 2 =x 2 −9 (2a+5b)(2a−5b)=(2a) 2 −(5b) 2 =4a 2 −25b 2 完全平方公式示例: (m+4) 2 =m 2 +2⋅m⋅4+4 2 =m 2 +8m+16 (3x−2y) 2 =(3x) 2 −2⋅3x⋅2y+(2y) 2 =9x 2 −12xy+4y 2 2. 变形应用:公式的逆用与拓展 公式变形 表达式 应用场景 平方差逆用 a 2 −b 2 =(a+b)(a−b) 因式分解、简便计算 完全平方逆用 a 2 ±2ab+b 2 =(a±b) 2 因式分解、配方 完全平方和差关系 (a+b) 2 −(a−b) 2 =4ab 求 ab 值 平方和公式 a 2 +b 2 =(a+b) 2 −2ab=(a−b) 2 +2ab 知和求平方和、知差求平方和 示例: 若 x+y=5 , xy=3 ,求 x 2 +y 2 x 2 +y 2 =(x+y) 2 −2xy=5 2 −2×3=25−6=19 3. 特殊形式应用(换元思想) 当公式中的 a 、 b 为多项式时,可将其视为一个整体套用公式: (a+b+c)(a+b−c)=[(a+b)+c][(a+b)−c]=(a+b) 2 −c 2 =a 2 +2ab+b 2 −c 2 (x−y+z) 2 =[(x−y)+z] 2 =(x−y) 2 +2(x−y)z+z 2 =x 2 −2xy+y 2 +2xz−2yz+z 2 4. 简便计算应用 利用公式简化复杂计算: 99×101=(100−1)(100+1)=100 2 −1 2 =10000−1=9999 102 2 =(100+2) 2 =100 2 +2×100×2+2 2 =10000+400+4=10404 99 2 =(100−1) 2 =100 2 −2×100×1+1 2 =10000−200+1=9801 四、常见题型分类解析 题型 解题关键 示例 公式直接计算 识别公式结构,找准 a 、 b (−2m−3n) 2 =(2m+3n) 2 =4m 2 +12mn+9n 2 公式逆用(因式分解) 识别平方差或完全平方式 x 2 −6x+9=(x−3) 2 条件求值 利用公式变形,整体代入 已知 a−b=3 ,求 a 2 +b 2 −6ab (变形为 (a−b) 2 −4ab ) 配方求最值 配成完全平方式,利用平方非负性 求 x 2 −4x+5 最小值(配方为 (x−2) 2 +1 ,最小值 1) 化简求值 先化简再代入,避免繁琐计算 化简 (2x+1) 2 −(2x−1) 2 ,再代入 x= 4 1 五、易错点警示与避错技巧 易错点 错误示例 正确做法 完全平方漏中间项 (a+b) 2 =a 2 +b 2 牢记 “首平方,尾平方,积的 2 倍在中央”,中间项为 2ab 完全平方符号错误 (a−b) 2 =a 2 −2ab−b 2 尾项平方恒为正,应为 a 2 −2ab+b 2 平方差公式误用 (a+b)(c−d)=a 2 −b 2 必须满足 “一项同,一项反”,不同则用多项式乘法 系数未平方 (2a) 2 =2a 2 系数与字母都要平方,应为 4a 2 符号处理错误 (−a−b) 2 =a 2 −2ab+b 2 提取负号再平方: (−a−b) 2 =(a+b) 2 =a 2 +2ab+b 2 避错口诀: 平方差:同方减反方,符号要对好 完全平方:和平方加两倍,差平方减两倍,尾项平方永为正 遇负号:先定号,再平方,避免符号乱 六、思维拓展:拓展乘法公式(选学) 三数和平方公式: (a+b+c) 2 =a 2 +b 2 +c 2 +2ab+2ac+2bc 立方和公式: (a+b)(a 2 −ab+b 2 )=a 3 +b 3 立方差公式: (a−b)(a 2 +ab+b 2 )=a 3 −b 3 总结 乘法公式是代数运算的基础工具,核心在于理解公式的结构特征与推导本质,而非死记硬背。通过大量练习掌握直接应用、逆用与变形应用,同时警惕常见易错点,就能熟练运用公式解决各类问题,为后续因式分解、二次函数等学习打下坚实基础。
![八年级数学 / 整式的乘法 / 整式的乘法
核心总览:整式乘法分为三大基础类型(单项式 × 单项式、单项式 × 多项式、多项式 × 多项式),以幂的运算法则为基础,延伸出平方差公式与完全平方公式两大常用乘法公式,运算时需注意符号与不漏项两大关键。
一、基础准备:幂的运算法则(必备前置知识)
法则 公式 示例 注意事项
同底数幂相乘
a
m
⋅a
n
=a
m+n
(
m,n
为正整数)
x
3
⋅x
5
=x
8
底数必须相同,指数相加
幂的乘方
(a
m
)
n
=a
mn
(y
2
)
4
=y
8
底数不变,指数相乘
积的乘方
(ab)
n
=a
n
b
n
(2x)
3
=8x
3
积中每个因式分别乘方
二、单项式与单项式相乘(整式乘法基础)
1. 运算法则
三步骤法:
系数相乘:按有理数乘法计算
同底数幂相乘:底数不变,指数相加
单独字母保留:只在一个单项式中出现的字母,连同指数作为积的因式
2. 典型例题
例 1:计算
2a
2
b⋅(−3ab
3
)
解:
(2×−3)⋅(a
2
⋅a)⋅(b⋅b
3
)=−6a
3
b
4
例 2:计算
(−2x
2
y)
3
⋅3xy
2
解:先算积的乘方:
(−2)
3
⋅(x
2
)
3
⋅y
3
=−8x
6
y
3
再相乘:
−8x
6
y
3
⋅3xy
2
=−24x
7
y
5
三、单项式与多项式相乘(转化思想的应用)
1. 运算法则
乘法分配律推广:用单项式乘多项式的每一项,再把所得的积相加公式:
m(a+b+c)=ma+mb+mc
2. 典型例题
例 3:计算
−2x(3x
2
−4x+1)
解:
−2x⋅3x
2
+(−2x)⋅(−4x)+(−2x)⋅1=−6x
3
+8x
2
−2x
3. 易错警示
符号问题:单项式为负时,每一项相乘都要变号
积的项数:结果项数与原多项式项数相同,防止漏乘
指数计算:单项式与多项式中同字母相乘时,指数相加而非相乘
四、多项式与多项式相乘(基础乘法的核心)
1. 运算法则
分步相乘再合并:先用一个多项式的每一项乘另一个多项式的每一项,再把所得积合并同类项公式:
(a+b)(m+n)=am+an+bm+bn
2. 典型例题
例 4:计算
(x+2)(2x−3)
解:
x⋅2x+x⋅(−3)+2⋅2x+2⋅(−3)
=2x
2
−3x+4x−6
=2x
2
+x−6
(合并同类项)
3. 常用技巧
网格法:将两个多项式的项写在网格的行与列,交叉相乘后求和
“首首末末” 法:先乘首尾项,再乘交叉项,最后合并
五、乘法公式(多项式乘法的特例,需熟练掌握)
1. 平方差公式
公式:
(a+b)(a−b)=a
2
−b
2
特点:两数和乘以两数差,结果为两数的平方差
例 5:
(3x+2)(3x−2)=(3x)
2
−2
2
=9x
2
−4
2. 完全平方公式
和的平方:
(a+b)
2
=a
2
+2ab+b
2
差的平方:
(a−b)
2
=a
2
−2ab+b
2
口诀:首平方,尾平方,积的 2 倍在中央,符号看中间
例 6:
(2x−5)
2
=(2x)
2
−2⋅2x⋅5+5
2
=4x
2
−20x+25
3. 公式应用注意事项
公式中的
a,b
可以是数字、字母或单项式 / 多项式
例:
(x+y+z)(x+y−z)=[(x+y)+z][(x+y)−z]=(x+y)
2
−z
2
(整体思想)
避免常见错误:
(a+b)
2
=a
2
+b
2
(漏掉中间的
2ab
)
(a−b)
2
=a
2
−b
2
(应为
a
2
−2ab+b
2
)
六、综合运算步骤与易错点汇总
1. 通用运算步骤
先算乘方(幂的运算),再算乘法,最后算加减(合并同类项)
有括号先算括号内,多重括号从内到外
能用乘法公式的优先使用公式简化计算](https://manimvideo.explanation.fun/video/cover/595293059794583553.png)
▶
八年级数学 / 整式的乘法 / 整式的乘法 核心总览:整式乘法分为三大基础类型(单项式 × 单项式、单项式 × 多项式、多项式 × 多项式),以幂的运算法则为基础,延伸出平方差公式与完全平方公式两大常用乘法公式,运算时需注意符号与不漏项两大关键。 一、基础准备:幂的运算法则(必备前置知识) 法则 公式 示例 注意事项 同底数幂相乘 a m ⋅a n =a m+n ( m,n 为正整数) x 3 ⋅x 5 =x 8 底数必须相同,指数相加 幂的乘方 (a m ) n =a mn (y 2 ) 4 =y 8 底数不变,指数相乘 积的乘方 (ab) n =a n b n (2x) 3 =8x 3 积中每个因式分别乘方 二、单项式与单项式相乘(整式乘法基础) 1. 运算法则 三步骤法: 系数相乘:按有理数乘法计算 同底数幂相乘:底数不变,指数相加 单独字母保留:只在一个单项式中出现的字母,连同指数作为积的因式 2. 典型例题 例 1:计算 2a 2 b⋅(−3ab 3 ) 解: (2×−3)⋅(a 2 ⋅a)⋅(b⋅b 3 )=−6a 3 b 4 例 2:计算 (−2x 2 y) 3 ⋅3xy 2 解:先算积的乘方: (−2) 3 ⋅(x 2 ) 3 ⋅y 3 =−8x 6 y 3 再相乘: −8x 6 y 3 ⋅3xy 2 =−24x 7 y 5 三、单项式与多项式相乘(转化思想的应用) 1. 运算法则 乘法分配律推广:用单项式乘多项式的每一项,再把所得的积相加公式: m(a+b+c)=ma+mb+mc 2. 典型例题 例 3:计算 −2x(3x 2 −4x+1) 解: −2x⋅3x 2 +(−2x)⋅(−4x)+(−2x)⋅1=−6x 3 +8x 2 −2x 3. 易错警示 符号问题:单项式为负时,每一项相乘都要变号 积的项数:结果项数与原多项式项数相同,防止漏乘 指数计算:单项式与多项式中同字母相乘时,指数相加而非相乘 四、多项式与多项式相乘(基础乘法的核心) 1. 运算法则 分步相乘再合并:先用一个多项式的每一项乘另一个多项式的每一项,再把所得积合并同类项公式: (a+b)(m+n)=am+an+bm+bn 2. 典型例题 例 4:计算 (x+2)(2x−3) 解: x⋅2x+x⋅(−3)+2⋅2x+2⋅(−3) =2x 2 −3x+4x−6 =2x 2 +x−6 (合并同类项) 3. 常用技巧 网格法:将两个多项式的项写在网格的行与列,交叉相乘后求和 “首首末末” 法:先乘首尾项,再乘交叉项,最后合并 五、乘法公式(多项式乘法的特例,需熟练掌握) 1. 平方差公式 公式: (a+b)(a−b)=a 2 −b 2 特点:两数和乘以两数差,结果为两数的平方差 例 5: (3x+2)(3x−2)=(3x) 2 −2 2 =9x 2 −4 2. 完全平方公式 和的平方: (a+b) 2 =a 2 +2ab+b 2 差的平方: (a−b) 2 =a 2 −2ab+b 2 口诀:首平方,尾平方,积的 2 倍在中央,符号看中间 例 6: (2x−5) 2 =(2x) 2 −2⋅2x⋅5+5 2 =4x 2 −20x+25 3. 公式应用注意事项 公式中的 a,b 可以是数字、字母或单项式 / 多项式 例: (x+y+z)(x+y−z)=[(x+y)+z][(x+y)−z]=(x+y) 2 −z 2 (整体思想) 避免常见错误: (a+b) 2 =a 2 +b 2 (漏掉中间的 2ab ) (a−b) 2 =a 2 −b 2 (应为 a 2 −2ab+b 2 ) 六、综合运算步骤与易错点汇总 1. 通用运算步骤 先算乘方(幂的运算),再算乘法,最后算加减(合并同类项) 有括号先算括号内,多重括号从内到外 能用乘法公式的优先使用公式简化计算
▶
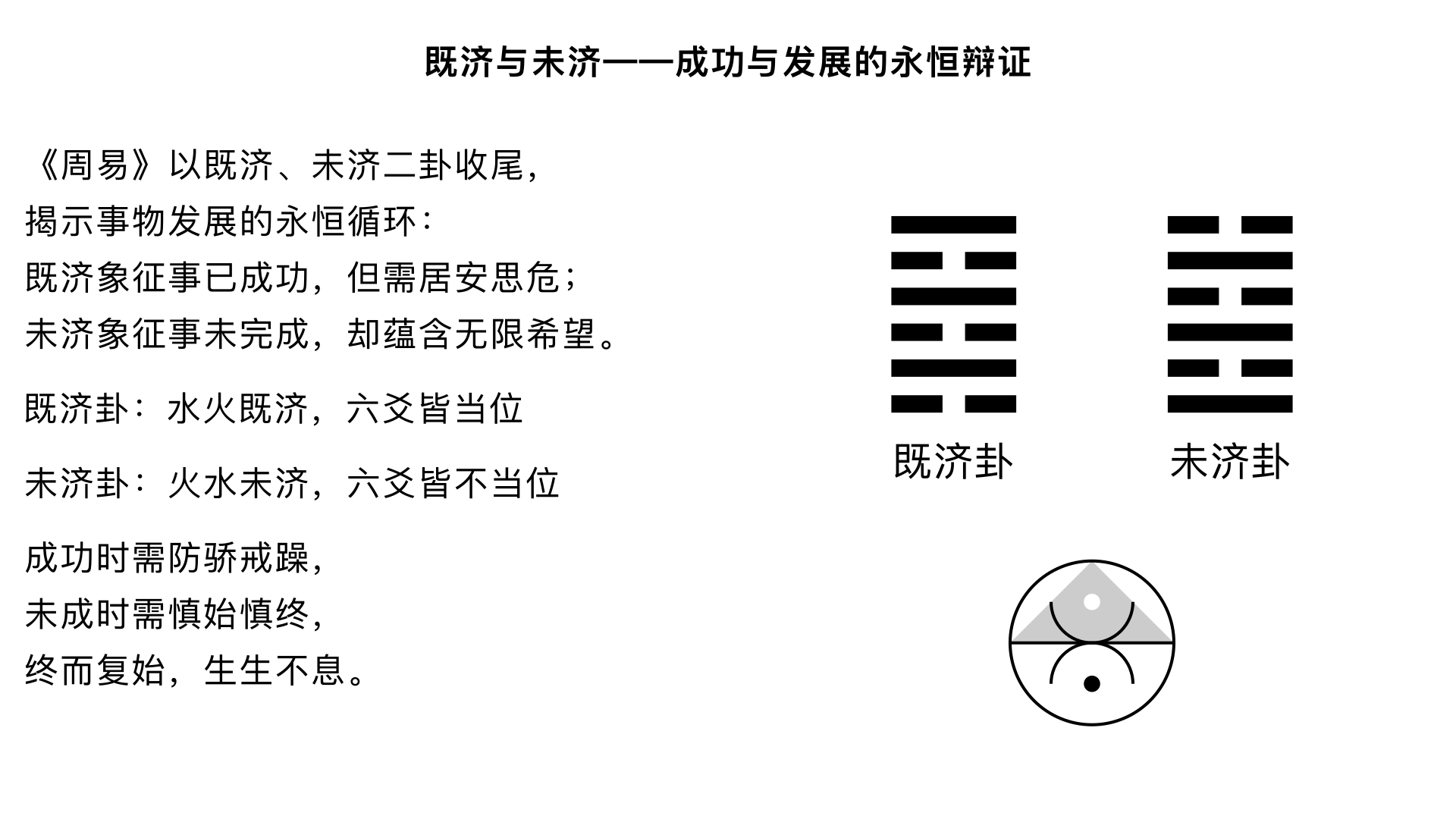
既济与未济——成功与发展的永恒辩证 一、既济卦(水火既济):事成守成之道 1. 卦序与卦象 《序卦传》:“有过物者必济,故受之以既济。” 能超越事物者必能成功。 卦象:上坎水,下离火(䷾),水在火上,水火相交,烹煮已成,象征事已成功。 爻象:六爻皆当位(阳在奇位,阴在偶位),且皆相应(初与四、二与五、三与上),是最完美的卦形。 2. 《彖传》精解 text 既济亨,小者亨也。 利贞,刚柔正而位当也。 初吉,柔得中也。 终止则乱,其道穷也。 “小者亨”:连小事也亨通(但大事未必)。 “刚柔正而位当”:六爻刚柔皆正且当位。 “初吉,柔得中也”:起初吉,因六二柔中。 “终止则乱”:若停止不前则生乱,因成功之道已穷尽。 3. 《大象传》:“水在火上,既济。君子以思患而豫防之。” 水在火上,事虽成但需防患;君子因此思虑后患而预先防备。 4. 爻辞精析 初九:曳其轮,濡其尾,无咎。 拖住车轮,沾湿尾巴,无咎(谨慎初始)。 六二:妇丧其茀,勿逐,七日得。 妇人丢失车帘,勿寻,七日后复得(守中待时)。 九三:高宗伐鬼方,三年克之,小人勿用。 高宗讨伐鬼方,三年取胜,小人不可用。 六四:繻有衣袽,终日戒。 华服会变破衣,终日戒备(居安思危)。 九五:东邻杀牛,不如西邻之禴祭,实受其福。 东邻杀牛厚祭,不如西邻薄祭,实际受福(诚胜于物)。 上六:濡其首,厉。 沾湿头部,危险(成功之后盲目冒进)。 二、未济卦(火水未济):未成发展之道 1. 卦序与卦象 《序卦传》:“物不可穷也,故受之以未济终焉。” 事物不可穷尽,所以以未济卦终结。 卦象:上离火,下坎水(䷿),火在水上,水火不相交,烹煮未成,象征事未成功。 爻象:六爻皆不当位(阳在偶位,阴在奇位),但皆相应(与既济正好相反)。 2. 《彖传》精解 text 未济亨,柔得中也。 小狐汔济,濡其尾,无攸利。 “柔得中也”:六五柔中。 “小狐汔济,濡其尾”:小狐几乎渡河,沾湿尾巴,无所利。 3. 《大象传》:“火在水上,未济。君子以慎辨物居方。” 火在水上,不相为用;君子因此谨慎辨别事物,使各居其所。 4. 爻辞精析 初六:濡其尾,吝。 沾湿尾巴,憾惜(贸然涉险)。 九二:曳其轮,贞吉。 拖住车轮,守正吉(谨慎而行)。 六三:未济,征凶,利涉大川。 事未成,出征凶,却利于涉越大河(看似矛盾,实则需勇气)。 九四:贞吉,悔亡。震用伐鬼方,三年有赏于大国。 守正吉,悔恨消失;如震动讨伐鬼方,三年获胜受赏。 六五:贞吉,无悔。君子之光,有孚吉。 守正吉,无悔;君子的光辉,有诚信则吉。 上九:有孚于饮酒,无咎。濡其首,有孚失是。 有诚信而饮酒,无咎;但若酗酒濡首,虽有诚信也失正。 三、既济未济的深刻哲学 《周易》的终始智慧:以未济卦结束,表明事物发展永无止境,终而复始。 成功与未成的辩证: 既济:完美但易止,需“思患豫防”。 未济:不完美但有希望,需“慎辨物居方”。 人生启示:成功时需防骄戒躁,未成时需慎始慎终。 金景芳总结:既济未济二卦,体现《周易》的变易哲学——既济是相对的完成,未济是永恒的发展;人生事业总是在“已成”与“未成”之间循环前进。
▶
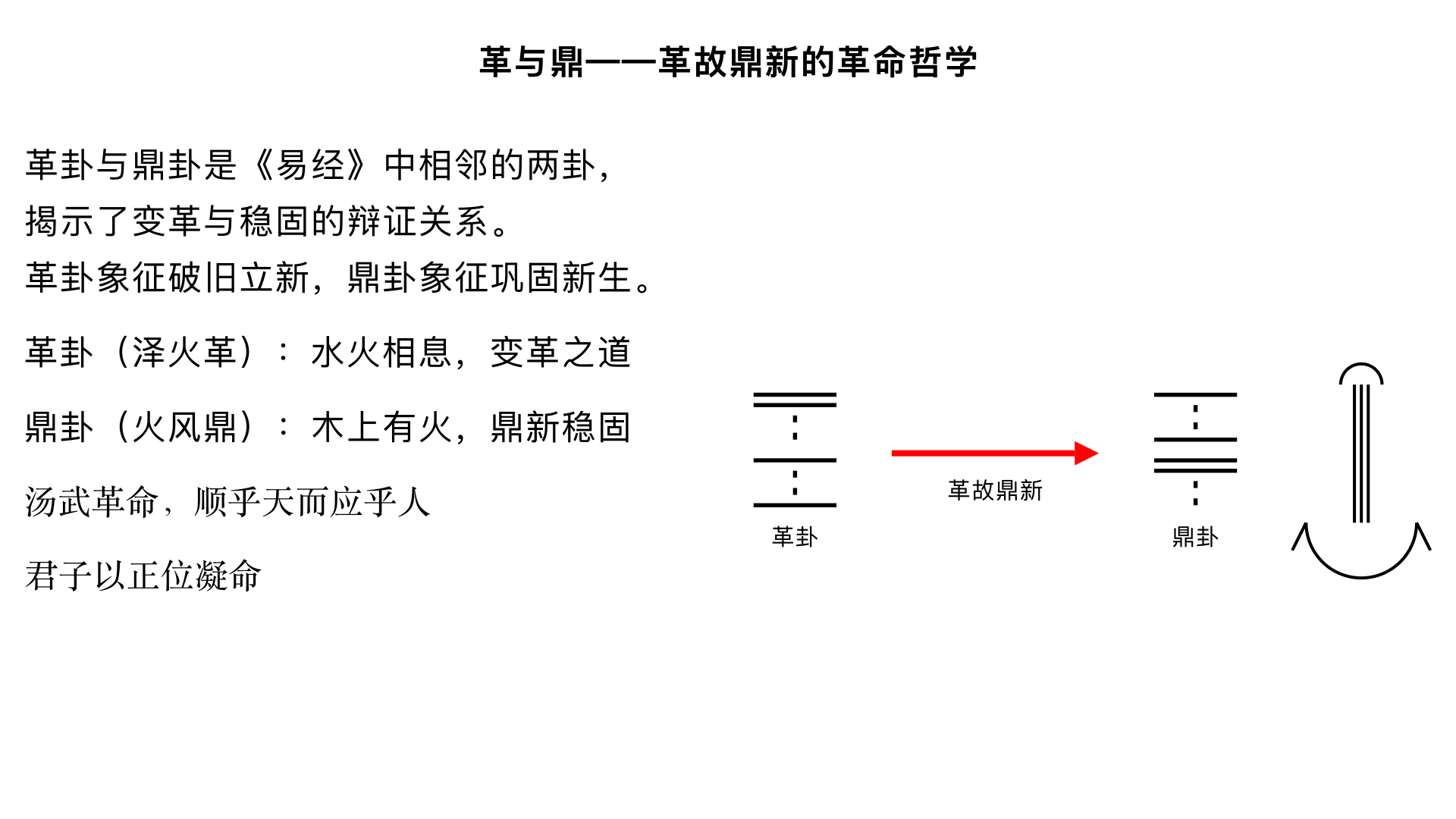
革与鼎——革故鼎新的革命哲学 一、革卦(泽火革):变革之道 1. 卦序与卦象 《序卦传》:“井道不可不革,故受之以革。” 井道需时常革新。 卦象:上兑泽,下离火(䷰),泽中有火,水灭火或火煮水,相互变革。 卦德:离明兑悦,文明而悦服地变革。 2. 《彖传》精解 text 革,水火相息,二女同居,其志不相得,曰革。 己日乃孚,革而信之。 文明以说,大亨以正,革而当,其悔乃亡。 天地革而四时成,汤武革命,顺乎天而应乎人。 革之时大矣哉! “水火相息”:水灭火,火煮水,相互更代。 “二女同居”:离为中女,兑为少女,同居而志不同,必生变革。 “己日乃孚”:在“己日”(转变之日)取信于人。 “汤武革命,顺乎天而应乎人”:商汤、周武的革命,顺天应人。 “革之时大矣哉”:变革的时势意义太重大了! 3. 《大象传》:“泽中有火,革。君子以治历明时。” 泽中有火,变革之象;君子因此修治历法,明辨时节(顺时应变)。 4. 爻辞精析 初九:巩用黄牛之革。 用黄牛皮革牢固束缚(变革之初宜稳固)。 六二:己日乃革之,征吉,无咎。 己日进行变革,出征吉,无咎。 九三:征凶,贞厉。革言三就,有孚。 出征凶,守正防危;变革之言多次审议,有诚信。 九四:悔亡,有孚改命,吉。 悔恨消失,有诚信改变旧命,吉。 九五:大人虎变,未占有孚。 大人如虎纹般变革,不占卜也知有诚信。 上六:君子豹变,小人革面,征凶,居贞吉。 君子如豹纹般变革,小人表面改变;出征凶,居守正得吉。 二、鼎卦(火风鼎):鼎新稳固之道 1. 卦序与卦象 《序卦传》:“革物者莫若鼎,故受之以鼎。” 变革事物没有比鼎更显著的(鼎用以烹煮,化生为熟)。 卦象:上离火,下巽木(䷱),木上有火,以鼎烹物。 卦形似鼎:初六像鼎足,九二、九三、九四像鼎腹,六五像鼎耳,上九像鼎铉。 卦德:巽入离明,以智慧洞察而入。 2. 《彖传》精解 text 鼎,象也。 以木巽火,亨饪也。 圣人亨以享上帝,而大亨以养圣贤。 巽而耳目聪明,柔进而上行,得中而应乎刚,是以元亨。 “鼎,象也”:鼎卦取象于鼎器。 “以木巽火,亨饪”:以木入火,烹煮食物。 “圣人亨以享上帝”:圣人烹煮以祭祀上帝。 “大亨以养圣贤”:大量烹煮以供养圣贤。 “巽而耳目聪明”:巽顺而离明,使人耳聪目明。 3. 《大象传》:“木上有火,鼎。君子以正位凝命。” 木上有火,鼎烹之象;君子因此端正位置,凝聚天命(巩固政权)。 4. 爻辞精析 初六:鼎颠趾,利出否。得妾以其子,无咎。 鼎脚颠倒,利于倒出污物;得妾因其子,无咎(破旧立新)。 九二:鼎有实,我仇有疾,不我能即,吉。 鼎中有实物,我的配偶有病,不能靠近我,吉(鼎实不虚,邪不干正)。 九三:鼎耳革,其行塞,雉膏不食,方雨亏悔,终吉。 鼎耳变革,行动受阻,野鸡汤吃不到;正遇雨减少悔恨,终吉。 九四:鼎折足,覆公餗,其形渥,凶。 鼎足折断,打翻王公美食,沾湿龌龊,凶(德薄位尊,不胜其任)。 六五:鼎黄耳金铉,利贞。 鼎有黄金耳、金属铉,利于守正(鼎器完美,象征位尊而柔中)。 上九:鼎玉铉,大吉,无不利。 鼎有玉铉,大吉无不利(温润高洁,举鼎自如)。 三、革鼎二卦的关联 革故与鼎新:革卦破除旧弊,鼎卦建立新秩序。 革命与守成:革卦强调“顺天应人”,鼎卦强调“正位凝命”。 政治寓意:汤武革命(革卦)后,制礼作乐、确立制度(鼎卦)。 金景芳阐述:革卦是激烈变革,鼎卦是稳固新生;二者是王朝兴替的两面,缺一不可。
▶
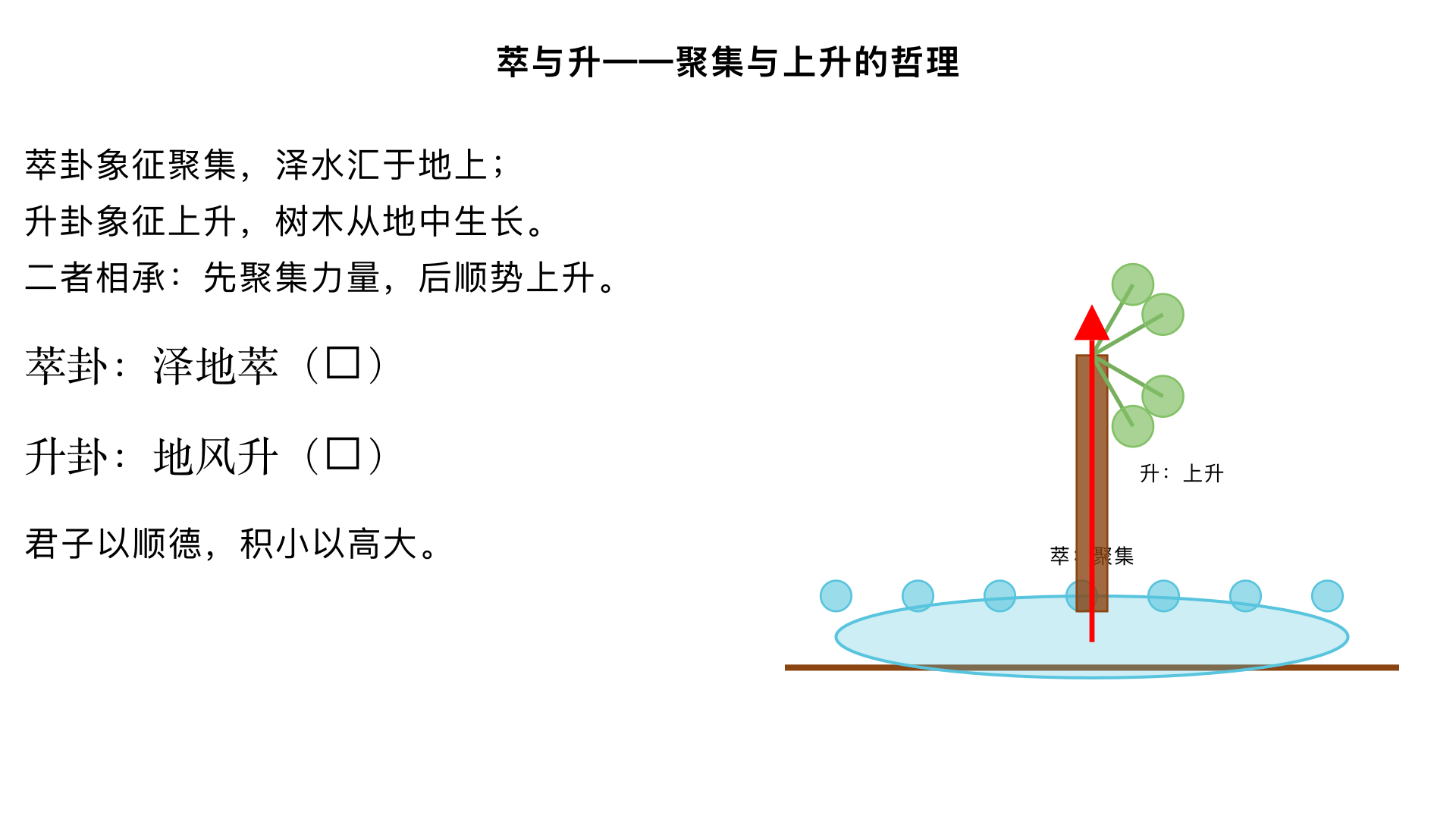
萃与升——聚集与上升的哲理 一、萃卦(泽地萃):荟萃凝聚之道 1. 卦序与卦象 《序卦传》:“姤者遇也,物相遇而后聚,故受之以萃。萃者,聚也。” 相遇之后聚集。 卦象:上兑泽,下坤地(䷬),泽在地上,水聚于地,象征聚集。 卦德:兑悦坤顺,和顺而喜悦相聚。 2. 《彖传》精解 text 萃,聚也。顺以说,刚中而应,故聚也。 王假有庙,致孝享也。 利见大人,亨,聚以正也。 用大牲吉,利有攸往,顺天命也。 观其所聚,而天地万物之情可见矣。 “顺以说,刚中而应”:下坤顺,上兑悦;九五刚中,与六二相应,故能聚集。 “王假有庙”:王至宗庙,致孝享祭祀。 “聚以正”:聚集需依正道。 “顺天命”:顺从天意而聚集。 “观其所聚…情可见”:观察聚集现象,可知天地万物之情。 3. 《大象传》:“泽上于地,萃。君子以除戎器,戒不虞。” 泽水聚于地上,有溃决之险;君子因此修治兵器,防备不测。 4. 爻辞精析 初六:有孚不终,乃乱乃萃。若号,一握为笑,勿恤,往无咎。 诚信不能始终,则聚会混乱;若呼号求应,可握手言笑,前往无咎。 六二:引吉,无咎,孚乃利用禴。 受人牵引而聚则吉,诚信即使薄祭也有利。 六三:萃如嗟如,无攸利。往无咎,小吝。 相聚却叹息,无利;前往无咎,但有小憾。 九四:大吉,无咎。 大吉而后无咎(因聚集得当)。 九五:萃有位,无咎。匪孚,元永贞,悔亡。 居位而聚,无咎;若未取信于人,则需永久守正以悔亡。 上六:赍咨涕洟,无咎。 悲叹涕泣(因孤高无应),但知惧则无咎。 二、升卦(地风升):顺势上升之道 1. 卦序与卦象 《序卦传》:“聚而上者谓之升,故受之以升。” 聚集后向上发展。 卦象:上坤地,下巽风(䷭),地中生木(巽为木),树木向上生长。 卦德:巽顺坤柔,以柔顺之道上升。 2. 《彖传》精解 text 柔以时升,巽而顺,刚中而应,是以大亨。 用见大人,勿恤,有庆也。 南征吉,志行也。 “柔以时升”:柔顺者依时上升。 “巽而顺,刚中而应”:下巽逊,上坤顺;九二刚中,与六五相应,故大亨通。 “南征吉”:向南行进吉(南为明方)。 3. 《大象传》:“地中生木,升。君子以顺德,积小以高大。” 地中生木,逐渐长高;君子效法,顺行其德,积小善以成高大。 4. 爻辞精析 初六:允升,大吉。 宜于上升,大吉。 九二:孚乃利用禴,无咎。 诚信即使薄祭也利,无咎。 九三:升虚邑。 上升如入无人之邑(畅通无阻)。 六四:王用亨于岐山,吉,无咎。 王在岐山祭祀,吉无咎(如文王祭岐山,象征获天命)。 六五:贞吉,升阶。 守正则吉,如升台阶(稳步上升)。 上六:冥升,利于不息之贞。 昏冥中仍上升,利于不停息地守正(但已至极点,宜守不宜进)。 三、萃升二卦的关联 聚而后升:萃卦是聚集人力物力,升卦是向上发展。 上升的条件:柔顺、诚信、守正、依时。 政治寓意:萃卦如招揽人才,升卦如任用贤能、事业上升。 金景芳强调:升卦强调“顺德,积小以高大”,反对急功近利,主张渐进积累。
▶
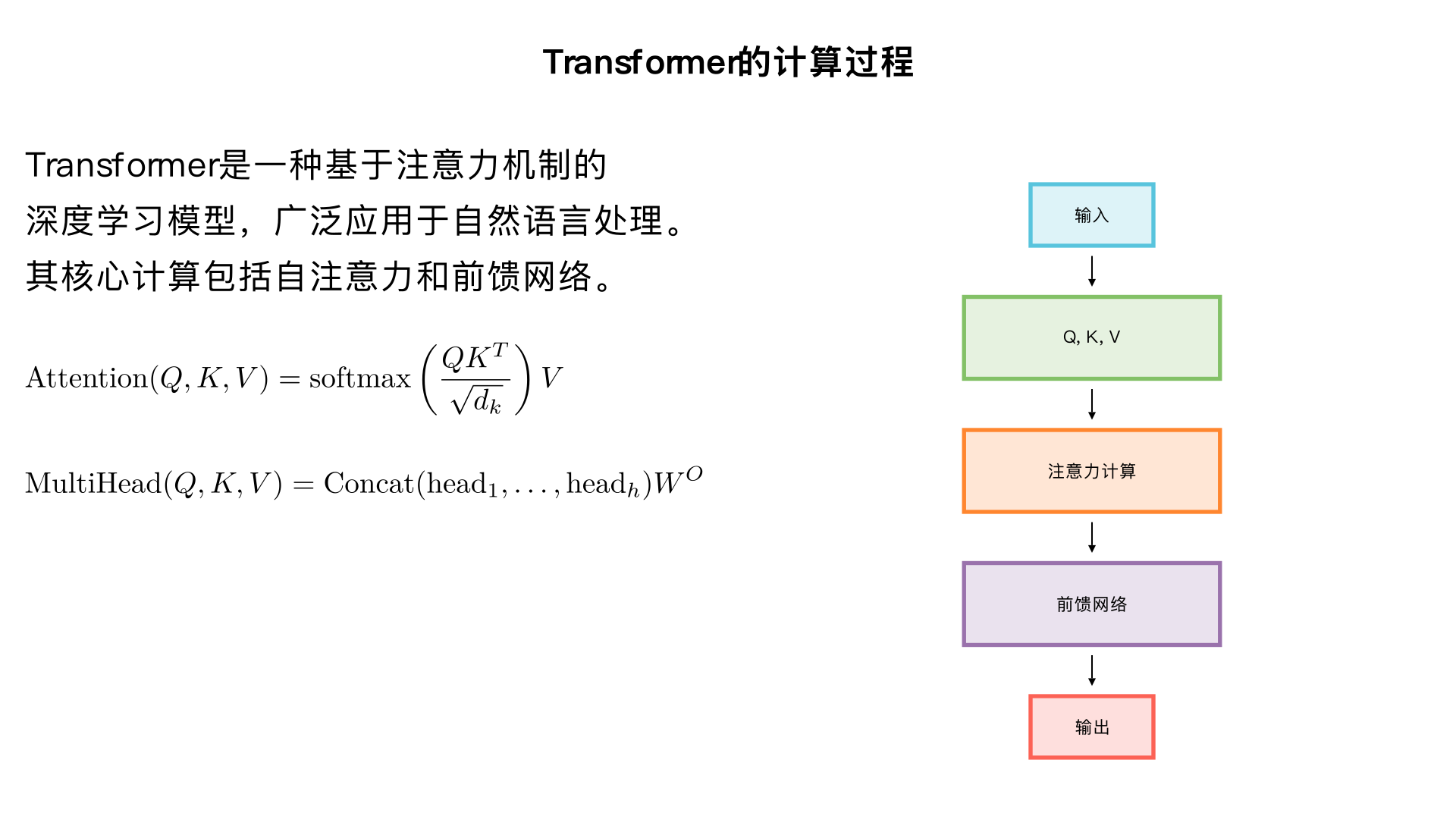
transformer的计算过程是什么?

▶
transformer的计算过程是什么?
▶
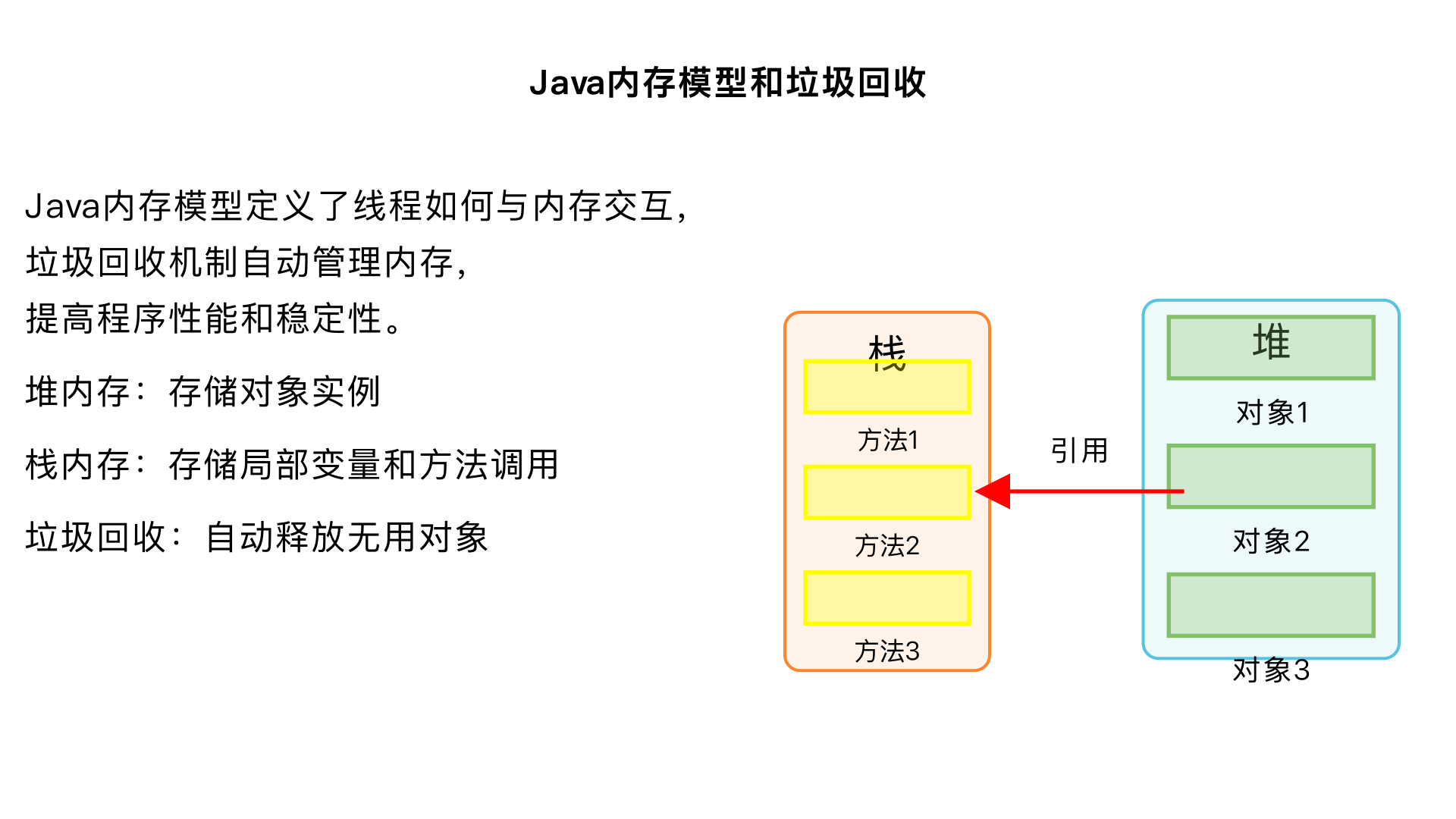
Java内存模型和垃圾回收
▶
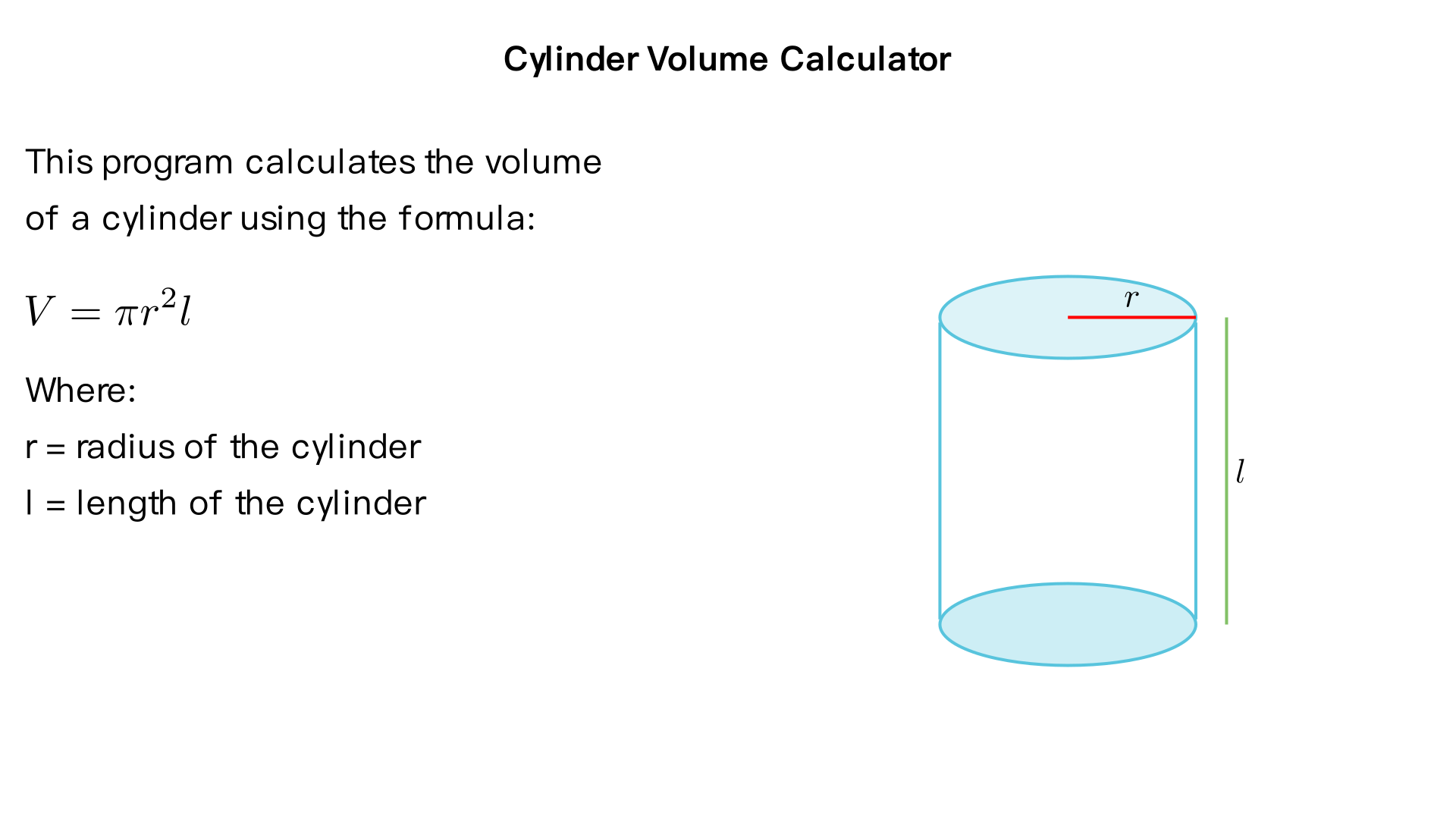
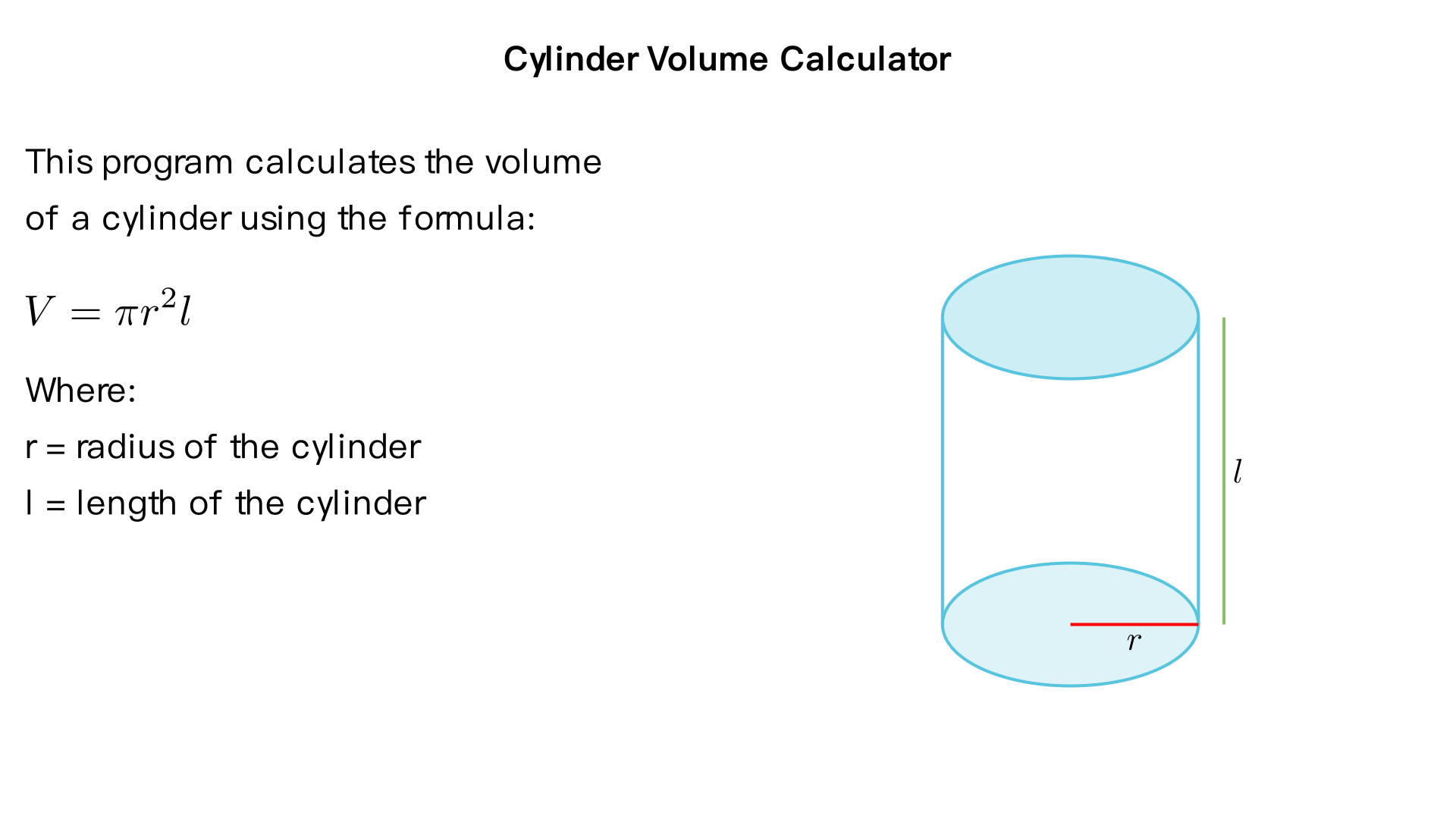
In the following questions, apply the design & development process. Give both the first and second level pseudocode and flowcharts with correct software flowchart symbol and right flow direction from begin to end, plus neccessary connection if one page is not enough for the flowchart, finally generrate C++ code for it: The volume of a cylinder is given by the following equation: volume = πr2l r is the radius, l is the length of the cylinder. Write a program that will prompt the user to enter the radius and the length of the cylinder. The program will calculate and display the volume
▶
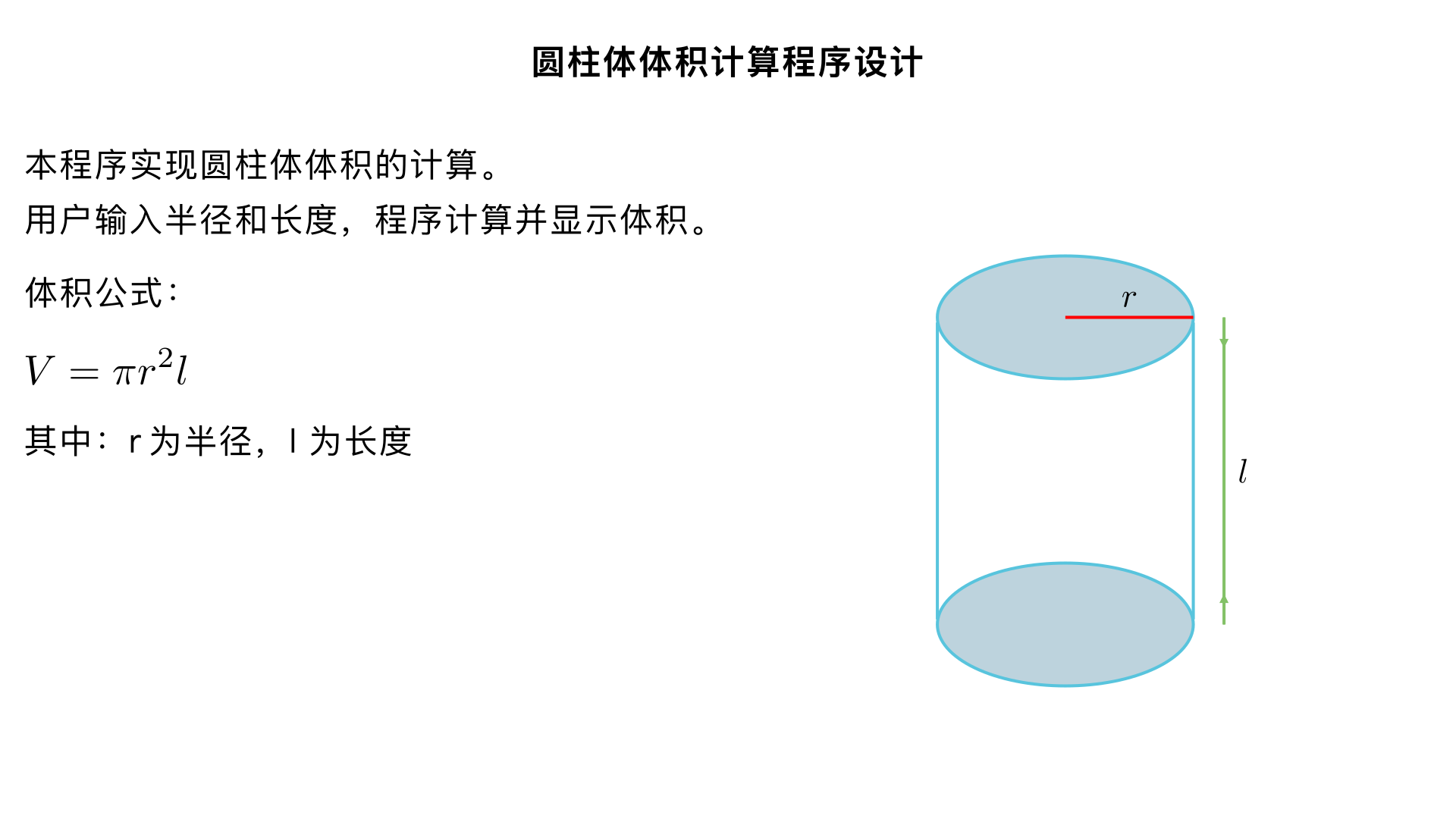
In the following questions, apply the design & development process. Give both the first and second level pseudocode and flowcharts with correct software flowchart symbol and right flow direction from begin to end, plus neccessary connection if one page is not enough for the flowchart, finally generrate C++ code for it: The volume of a cylinder is given by the following equation: volume = πr2l r is the radius, l is the length of the cylinder. Write a program that will prompt the user to enter the radius and the length of the cylinder. The program will calculate and display the volume
▶