T
Teach Me AnythingTMA
Video History
Page 7 / 44
▶
帮我生成一个视频,小女孩微笑,发出一个元旦祝福,家人鼓掌,要求3秒,画面清晰流畅美观
▶
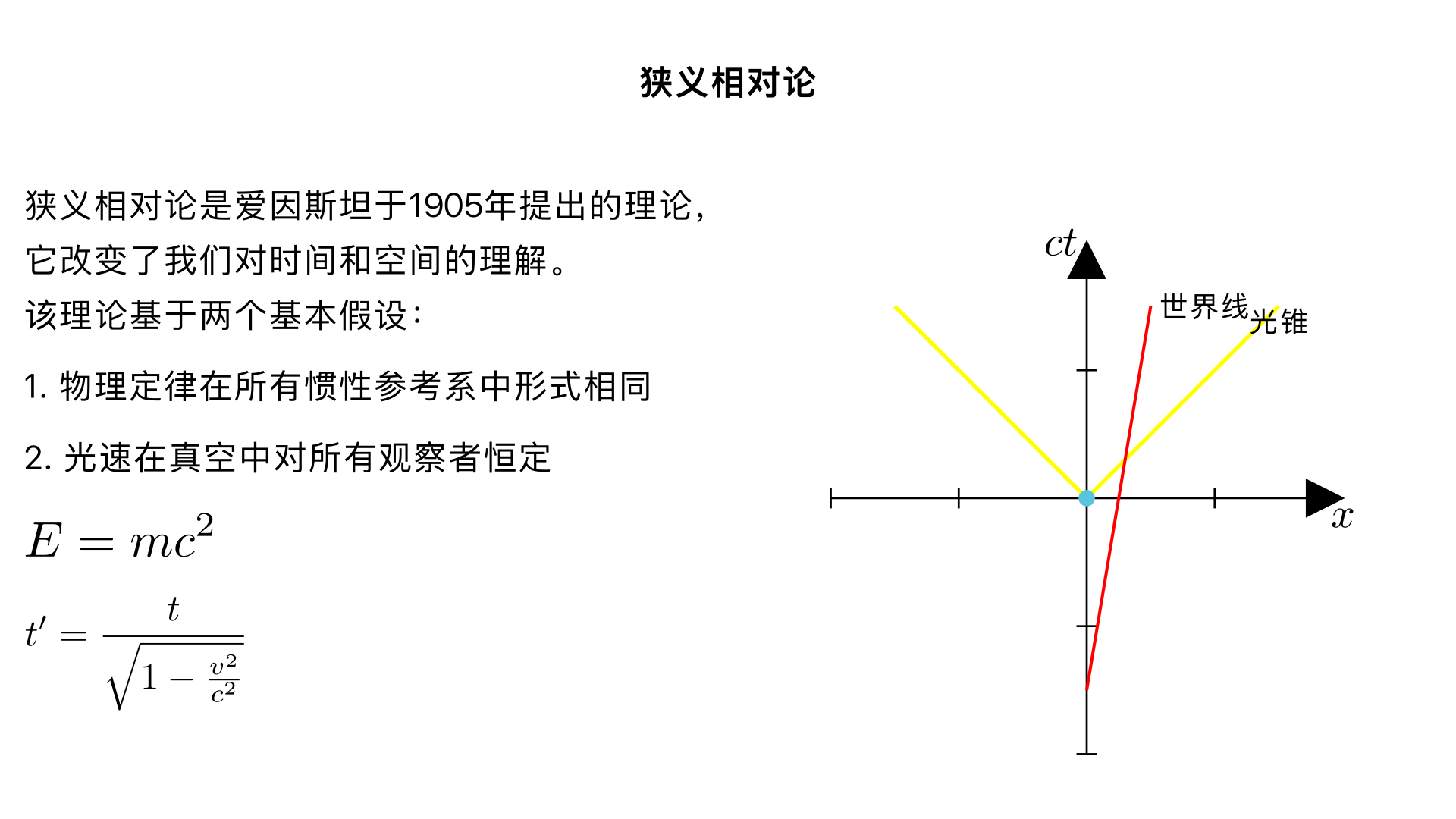
介绍一下狭义相对论
▶
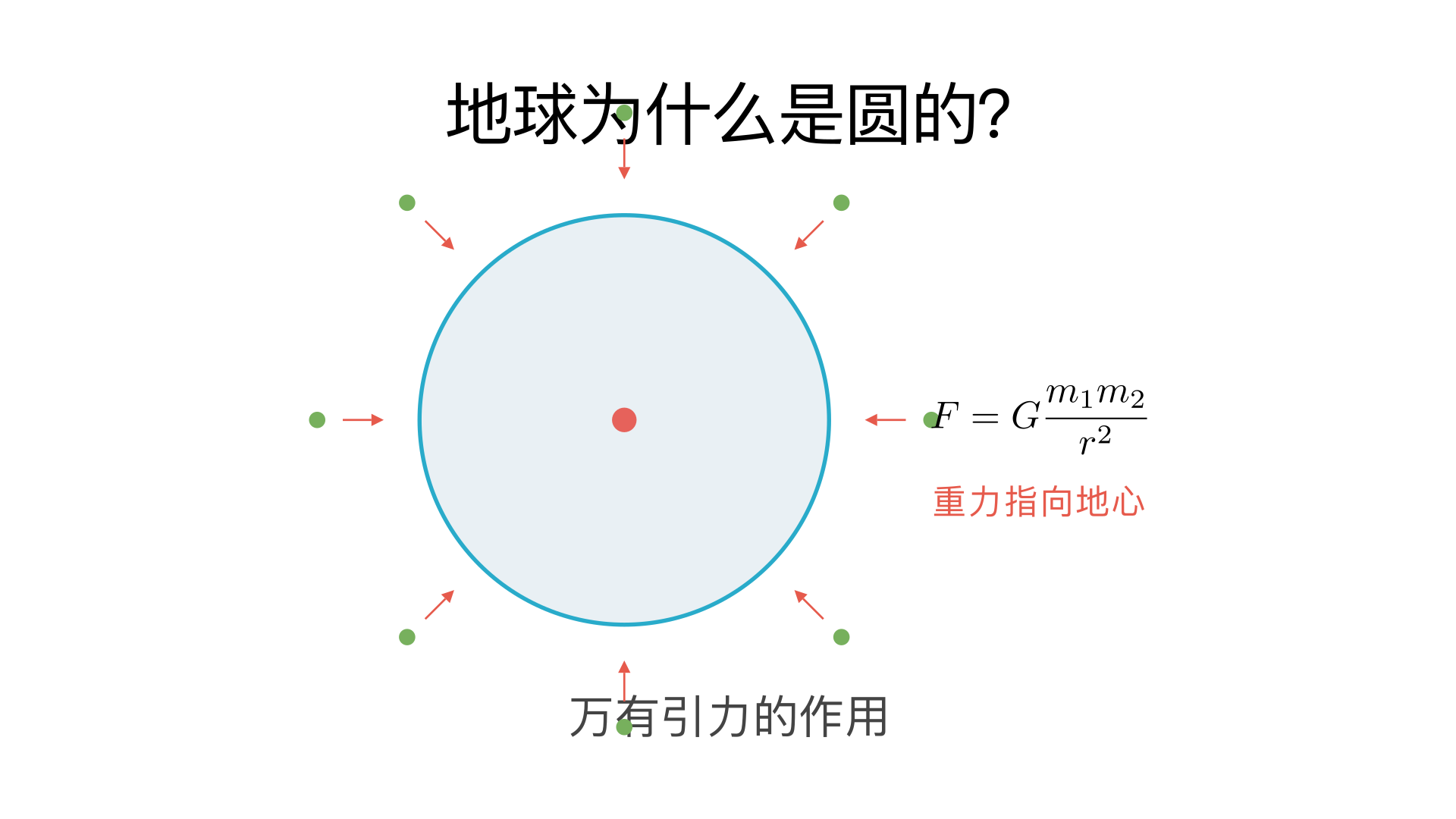
地球为什么是圆的
![八年级数学 / 因式分解 / 用公式法分解因式
一、知识框架(符合教学大纲核心要求)
公式法分解因式的定义:利用乘法公式的逆运算,将多项式分解为几个整式乘积的形式(本质是 “和差化积”,与整式乘法 “积化和差” 互为逆过程)。
核心公式(八年级必掌握 2 个基础公式):
平方差公式
完全平方公式
适用条件:多项式需符合对应公式的结构特征,无需先提公因式(若有公因式需先提公因式,再用公式法)。
核心步骤:判断结构→匹配公式→验证结果→分解彻底。
二、核心公式详解(含结构特征 + 易错点)
(一)平方差公式
1. 公式形式
a
2
−b
2
=(a+b)(a−b)
(文字表述:两个数的平方差,等于这两个数的和与这两个数的差的积)
2. 结构特征(3 个关键条件,缺一不可)
多项式是二项式(只有两项);
两项的符号一正一负(必须是 “差” 的形式,不能是 “和”);
每一项都能写成某个整式的平方形式(含数字系数、字母、多项式整体的平方)。
3. 常见易错点
忽略数字系数的平方:如
4x
2
−9
,需先转化为
(2x)
2
−3
2
,再套用公式;
误用于 “平方和”:如
x
2
+4
不能用平方差公式分解(无实数解,八年级阶段不分解);
分解不彻底:如
x
4
−16
,需先分解为
(x
2
+4)(x
2
−1)
,再对
x
2
−1
继续分解为
(x+1)(x−1)
,最终结果为
(x
2
+4)(x+1)(x−1)
。
4. 典型例题
基础题:分解
x
2
−16
解:
x
2
−16=x
2
−4
2
=(x+4)(x−4)
数字系数含平方:分解
25a
2
−4b
2
解:
25a
2
−4b
2
=(5a)
2
−(2b)
2
=(5a+2b)(5a−2b)
多项式整体为平方:分解
(x+2)
2
−9
解:
(x+2)
2
−9=(x+2)
2
−3
2
=[(x+2)+3][(x+2)−3]=(x+5)(x−1)
分解彻底:分解
16x
4
−y
4
解:
16x
4
−y
4
=(4x
2
)
2
−(y
2
)
2
=(4x
2
+y
2
)(4x
2
−y
2
)=(4x
2
+y
2
)(2x+y)(2x−y)
(二)完全平方公式
1. 公式形式(两式:和的平方、差的平方)
a
2
+2ab+b
2
=(a+b)
2
a
2
−2ab+b
2
=(a−b)
2
(文字表述:两个数的平方和,加上或减去这两个数乘积的 2 倍,等于这两个数的和或差的平方)
2. 结构特征(3 个关键条件,缺一不可)
多项式是三项式(含三项,核心是 “首尾平方项 + 中间交叉项”);
首尾两项是非负的平方形式(符号相同,可提取负号后转化为平方,如
−x
2
+2xy−y
2
=−(x
2
−2xy+y
2
)
);
中间项是首尾两项底数乘积的 2 倍(符号与公式中的 “±” 一致,即和的平方中间为正,差的平方中间为负)。
3. 记忆口诀(帮你快速判断)
“首平方,尾平方,首尾乘积的 2 倍在中央,符号看前方,完全平方把名扬”。
4. 常见易错点
中间项漏乘 2:如
x
2
+xy+y
2
不是完全平方式(中间项应为
2xy
);
首尾项不是平方数:如
x
2
+6x+8
(尾项 8 不是平方数,不能用完全平方公式);
符号判断错误:如
x
2
−8x+16
,中间项为负,对应 “差的平方”,分解为
(x−4)
2
;
首项系数不为 1 时忽略转化:如
4x
2
−12xy+9y
2
,需先转化为
(2x)
2
−2⋅2x⋅3y+(3y)
2
,再套用公式。
5. 典型例题
基础题(和的平方):分解
x
2
+10x+25
解:
x
2
+10x+25=x
2
+2⋅x⋅5+5
2
=(x+5)
2
基础题(差的平方):分解
a
2
−8a+16
解:
a
2
−8a+16=a
2
−2⋅a⋅4+4
2
=(a−4)
2
首项系数不为 1:分解
9x
2
+12xy+4y
2
解:
9x
2
+12xy+4y
2
=(3x)
2
+2⋅3x⋅2y+(2y)
2
=(3x+2y)
2
含负号:分解
−x
2
+6xy−9y
2
解:先提取负号→
−(x
2
−6xy+9y
2
)=−[x
2
−2⋅x⋅3y+(3y)
2
]=−(x−3y)
2
三、公式法分解因式的核心步骤(通用流程)
先提公因式:若多项式各项有公因式,先提取公因式(如
2x
2
−8=2(x
2
−4)
,再对
x
2
−4
用平方差公式);
判断结构:
二项式→看是否为 “平方差”(一正一负、两项均为平方);
三项式→看是否为 “完全平方式”(首尾平方、中间 2 倍乘积);
套用公式:根据结构匹配对应公式,注意符号和系数的转化;
验证彻底:分解后检查每个因式是否还能继续分解(如
x
4
−1
需分解到
(x
2
+1)(x+1)(x−1)
);
检验结果:用整式乘法逆推验证(如
(x+3)(x−3)=x
2
−9
,与原式一致则正确)。
四、综合练习题(基础→提升,附解析思路)
1. 基础题(直接套用公式)
(平方差)
m
2
−9n
2
→ 思路:
(m)
2
−(3n)
2
=(m+3n)(m−3n)
(完全平方)
x
2
−12x+36
→ 思路:
x
2
−2⋅x⋅6+6
2
=(x−6)
2
2. 提升题(先提公因式 + 公式)
3a
3
−12a
→ 思路:先提
3a
→
3a(a
2
−4)
,再用平方差→
3a(a+2)(a−2)
2x
2
y−8xy+8y
→ 思路:先提
2y
→
2y(x
2
−4x+4)
,再用完全平方→
2y(x−2)
2
3. 拓展题(多项式整体为底数)
(a+b)
2
−(c−d)
2
→ 思路:平方差公式→
[(a+b)+(c−d)][(a+b)−(c−d)]=(a+b+c−d)(a+b−c+d)
(x
2
+1)
2
−4x
2
→ 思路:平方差→
[(x
2
+1)+2x][(x
2
+1)−2x]=(x+1)
2
(x−1)
2
(后续两个因式均为完全平方式)
五、中考高频考点总结
公式的灵活运用:尤其是含数字系数、多项式底数的分解(如
(2x−y)
2
−(x+2y)
2
);
分解彻底的要求:中考评分标准中,未分解彻底不得满分(如
x
4
−16
只分解到
(x
2
+4)(x
2
−4)
得一半分);
与其他知识点结合:常与一元二次方程、分式化简、代数式求值结合(如先分解因式再代入计算:已知
x+y=5
,
x−y=3
,求
x
2
−y
2
的值→分解为
(x+y)(x−y)=5×3=15
)。](https://manimvideo.explanation.fun/video/cover/596386302997843969.png)
▶
八年级数学 / 因式分解 / 用公式法分解因式 一、知识框架(符合教学大纲核心要求) 公式法分解因式的定义:利用乘法公式的逆运算,将多项式分解为几个整式乘积的形式(本质是 “和差化积”,与整式乘法 “积化和差” 互为逆过程)。 核心公式(八年级必掌握 2 个基础公式): 平方差公式 完全平方公式 适用条件:多项式需符合对应公式的结构特征,无需先提公因式(若有公因式需先提公因式,再用公式法)。 核心步骤:判断结构→匹配公式→验证结果→分解彻底。 二、核心公式详解(含结构特征 + 易错点) (一)平方差公式 1. 公式形式 a 2 −b 2 =(a+b)(a−b) (文字表述:两个数的平方差,等于这两个数的和与这两个数的差的积) 2. 结构特征(3 个关键条件,缺一不可) 多项式是二项式(只有两项); 两项的符号一正一负(必须是 “差” 的形式,不能是 “和”); 每一项都能写成某个整式的平方形式(含数字系数、字母、多项式整体的平方)。 3. 常见易错点 忽略数字系数的平方:如 4x 2 −9 ,需先转化为 (2x) 2 −3 2 ,再套用公式; 误用于 “平方和”:如 x 2 +4 不能用平方差公式分解(无实数解,八年级阶段不分解); 分解不彻底:如 x 4 −16 ,需先分解为 (x 2 +4)(x 2 −1) ,再对 x 2 −1 继续分解为 (x+1)(x−1) ,最终结果为 (x 2 +4)(x+1)(x−1) 。 4. 典型例题 基础题:分解 x 2 −16 解: x 2 −16=x 2 −4 2 =(x+4)(x−4) 数字系数含平方:分解 25a 2 −4b 2 解: 25a 2 −4b 2 =(5a) 2 −(2b) 2 =(5a+2b)(5a−2b) 多项式整体为平方:分解 (x+2) 2 −9 解: (x+2) 2 −9=(x+2) 2 −3 2 =[(x+2)+3][(x+2)−3]=(x+5)(x−1) 分解彻底:分解 16x 4 −y 4 解: 16x 4 −y 4 =(4x 2 ) 2 −(y 2 ) 2 =(4x 2 +y 2 )(4x 2 −y 2 )=(4x 2 +y 2 )(2x+y)(2x−y) (二)完全平方公式 1. 公式形式(两式:和的平方、差的平方) a 2 +2ab+b 2 =(a+b) 2 a 2 −2ab+b 2 =(a−b) 2 (文字表述:两个数的平方和,加上或减去这两个数乘积的 2 倍,等于这两个数的和或差的平方) 2. 结构特征(3 个关键条件,缺一不可) 多项式是三项式(含三项,核心是 “首尾平方项 + 中间交叉项”); 首尾两项是非负的平方形式(符号相同,可提取负号后转化为平方,如 −x 2 +2xy−y 2 =−(x 2 −2xy+y 2 ) ); 中间项是首尾两项底数乘积的 2 倍(符号与公式中的 “±” 一致,即和的平方中间为正,差的平方中间为负)。 3. 记忆口诀(帮你快速判断) “首平方,尾平方,首尾乘积的 2 倍在中央,符号看前方,完全平方把名扬”。 4. 常见易错点 中间项漏乘 2:如 x 2 +xy+y 2 不是完全平方式(中间项应为 2xy ); 首尾项不是平方数:如 x 2 +6x+8 (尾项 8 不是平方数,不能用完全平方公式); 符号判断错误:如 x 2 −8x+16 ,中间项为负,对应 “差的平方”,分解为 (x−4) 2 ; 首项系数不为 1 时忽略转化:如 4x 2 −12xy+9y 2 ,需先转化为 (2x) 2 −2⋅2x⋅3y+(3y) 2 ,再套用公式。 5. 典型例题 基础题(和的平方):分解 x 2 +10x+25 解: x 2 +10x+25=x 2 +2⋅x⋅5+5 2 =(x+5) 2 基础题(差的平方):分解 a 2 −8a+16 解: a 2 −8a+16=a 2 −2⋅a⋅4+4 2 =(a−4) 2 首项系数不为 1:分解 9x 2 +12xy+4y 2 解: 9x 2 +12xy+4y 2 =(3x) 2 +2⋅3x⋅2y+(2y) 2 =(3x+2y) 2 含负号:分解 −x 2 +6xy−9y 2 解:先提取负号→ −(x 2 −6xy+9y 2 )=−[x 2 −2⋅x⋅3y+(3y) 2 ]=−(x−3y) 2 三、公式法分解因式的核心步骤(通用流程) 先提公因式:若多项式各项有公因式,先提取公因式(如 2x 2 −8=2(x 2 −4) ,再对 x 2 −4 用平方差公式); 判断结构: 二项式→看是否为 “平方差”(一正一负、两项均为平方); 三项式→看是否为 “完全平方式”(首尾平方、中间 2 倍乘积); 套用公式:根据结构匹配对应公式,注意符号和系数的转化; 验证彻底:分解后检查每个因式是否还能继续分解(如 x 4 −1 需分解到 (x 2 +1)(x+1)(x−1) ); 检验结果:用整式乘法逆推验证(如 (x+3)(x−3)=x 2 −9 ,与原式一致则正确)。 四、综合练习题(基础→提升,附解析思路) 1. 基础题(直接套用公式) (平方差) m 2 −9n 2 → 思路: (m) 2 −(3n) 2 =(m+3n)(m−3n) (完全平方) x 2 −12x+36 → 思路: x 2 −2⋅x⋅6+6 2 =(x−6) 2 2. 提升题(先提公因式 + 公式) 3a 3 −12a → 思路:先提 3a → 3a(a 2 −4) ,再用平方差→ 3a(a+2)(a−2) 2x 2 y−8xy+8y → 思路:先提 2y → 2y(x 2 −4x+4) ,再用完全平方→ 2y(x−2) 2 3. 拓展题(多项式整体为底数) (a+b) 2 −(c−d) 2 → 思路:平方差公式→ [(a+b)+(c−d)][(a+b)−(c−d)]=(a+b+c−d)(a+b−c+d) (x 2 +1) 2 −4x 2 → 思路:平方差→ [(x 2 +1)+2x][(x 2 +1)−2x]=(x+1) 2 (x−1) 2 (后续两个因式均为完全平方式) 五、中考高频考点总结 公式的灵活运用:尤其是含数字系数、多项式底数的分解(如 (2x−y) 2 −(x+2y) 2 ); 分解彻底的要求:中考评分标准中,未分解彻底不得满分(如 x 4 −16 只分解到 (x 2 +4)(x 2 −4) 得一半分); 与其他知识点结合:常与一元二次方程、分式化简、代数式求值结合(如先分解因式再代入计算:已知 x+y=5 , x−y=3 ,求 x 2 −y 2 的值→分解为 (x+y)(x−y)=5×3=15 )。
▶
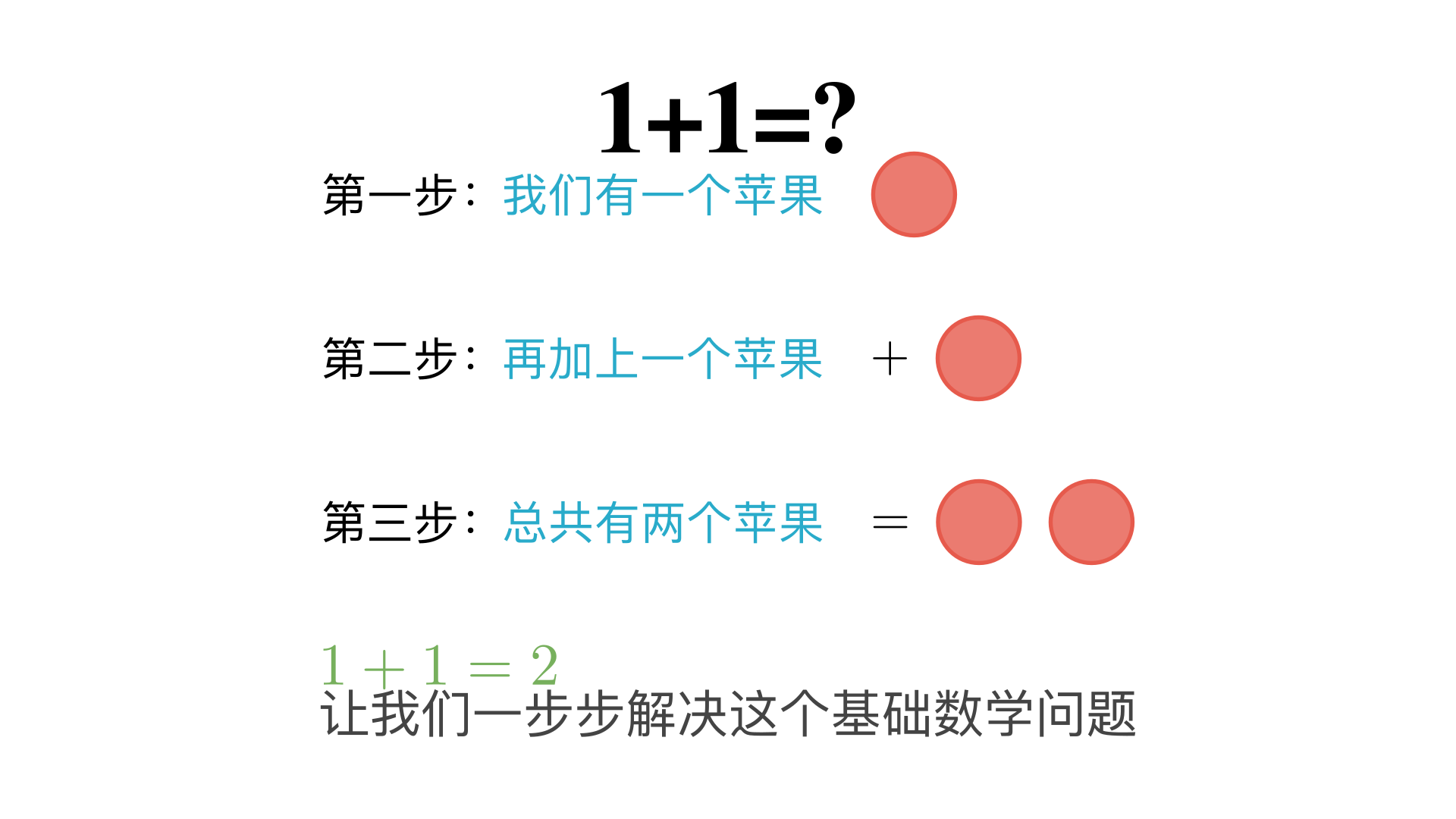
1+1=?
▶
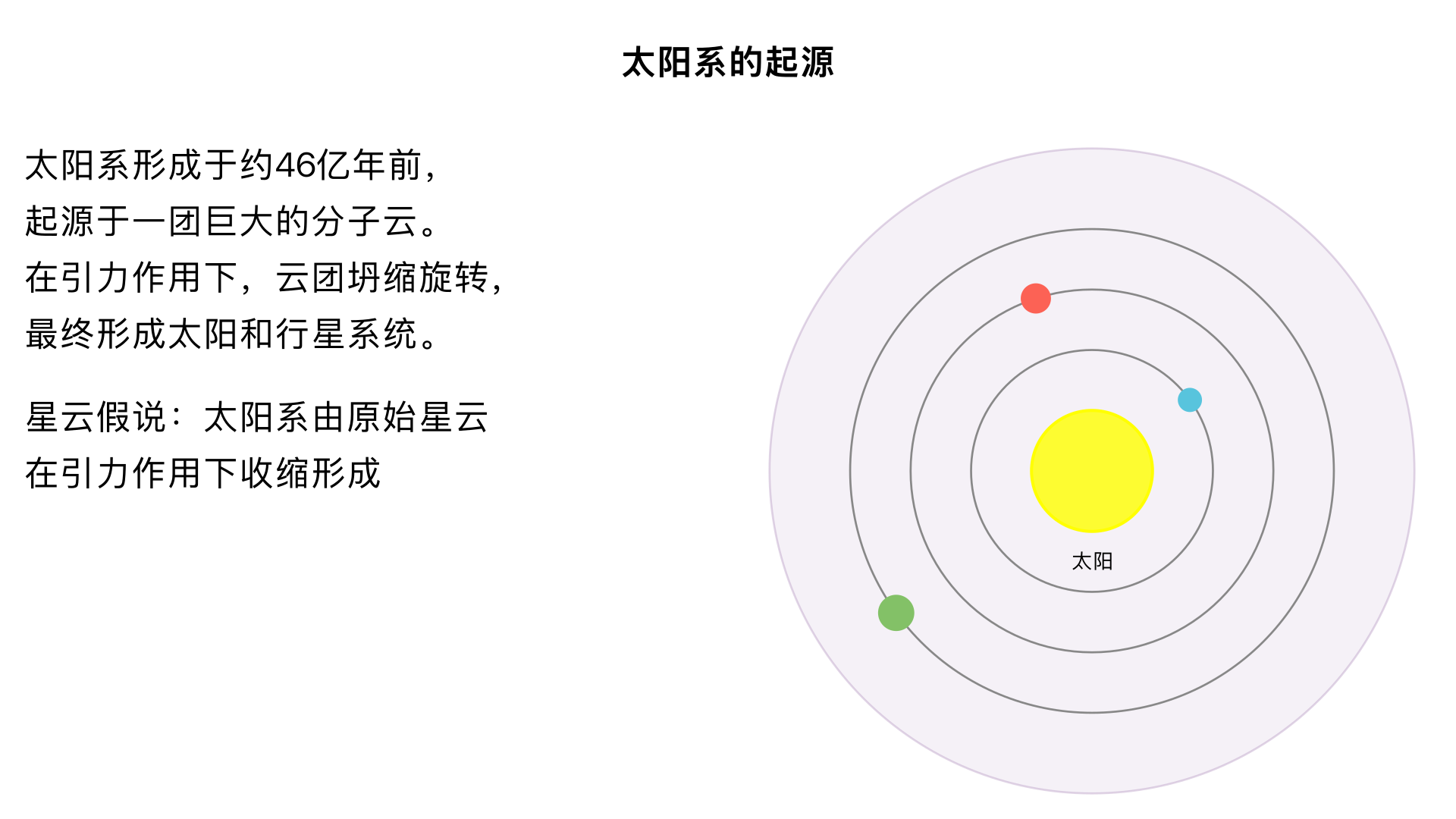
太阳系的起源
▶
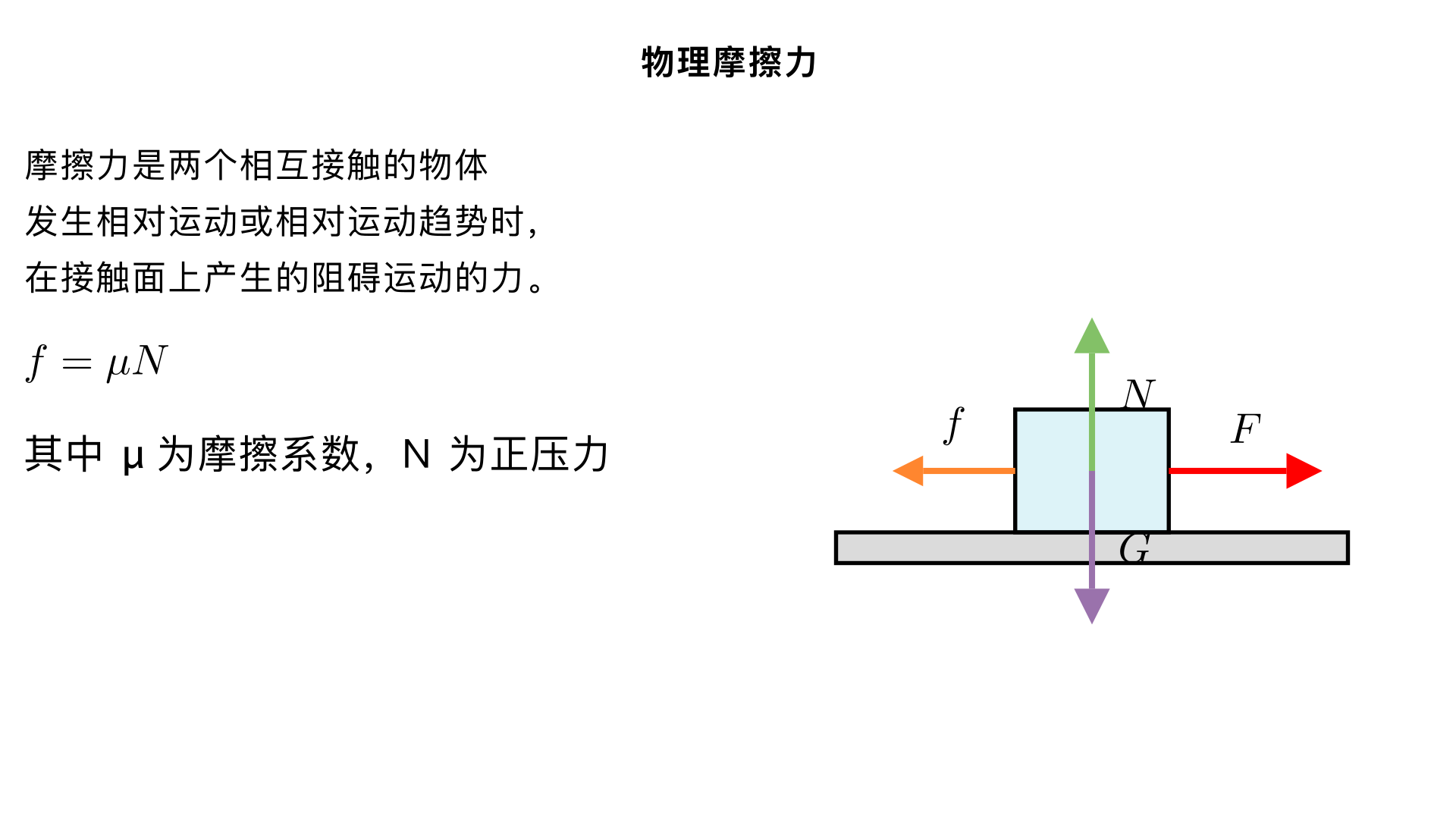
请生成一个解释物理摩擦力的视频
![八年级数学 / 因式分解 / 用提公因式法分解因式
一、核心概念(夯实基础)
1. 公因式的定义
一个多项式中各项都含有的公共因式,叫做这个多项式各项的公因式。
公因式的构成:① 系数部分:各项系数的最大公约数(若系数为负,取绝对值的最大公约数,最终公因式的符号由多项式首项符号决定,通常使首项为正);② 字母部分:各项中相同的字母,且取相同字母的最低次幂;③ 特殊情况:公因式可以是单项式,也可以是多项式(如
(a+b)
作为公共因式)。
示例:多项式
8a
3
b
2
−12ab
3
c
的公因式:系数部分:8 和 12 的最大公约数是 4;字母部分:相同字母为
a
(最低次幂
a
1
)、
b
(最低次幂
b
2
),无公共字母
c
;因此公因式为
4ab
2
。
2. 提公因式法的定义
如果一个多项式的各项含有公因式,那么就可以把这个公因式提取出来,将多项式化成两个因式乘积的形式,这种因式分解的方法叫做提公因式法。
本质:逆用乘法分配律(
ma+mb+mc=m(a+b+c)
,其中
m
为公因式)。
二、提公因式法的解题步骤(规范操作)
步骤 1:找公因式(关键步骤)
按 “系数→字母→多项式” 的顺序找,确保不遗漏:① 找系数的最大公约数(含符号处理);② 找相同字母的最低次幂;③ 若各项含有相同的多项式因式,将其视为一个整体作为公因式。
步骤 2:提公因式
用多项式的每一项除以公因式,得到另一个因式,公因式写在括号外,两个因式用乘法连接。
注意:提取公因式后,括号内的各项系数、字母次数要与原多项式对应,不能漏项。
步骤 3:验结果(避免出错)
用乘法分配律将分解后的式子展开,看是否与原多项式相等,若相等则分解正确。
三、典型例题(分层突破)
类型 1:公因式为单项式(基础题)
例 1:分解因式
6x
2
y−9xy
2
+3xy
步骤 1:找公因式
系数:6、-9、3 的最大公约数是 3;
字母:相同字母
x
(最低次幂
x
1
)、
y
(最低次幂
y
1
);
公因式为
3xy
。
步骤 2:提公因式
每一项除以
3xy
:
6x
2
y÷3xy=2x
,
−9xy
2
÷3xy=−3y
,
3xy÷3xy=1
;
因此分解结果:
3xy(2x−3y+1)
(注意:最后一项除以公因式得 1,不能漏写)。
步骤 3:验证
展开
3xy(2x−3y+1)=6x
2
y−9xy
2
+3xy
,与原多项式一致,正确。
例 2:分解因式
−4a
3
b
2
+6a
2
b−2ab
步骤 1:找公因式
首项为负,先提取 “-” 号,再找系数绝对值的最大公约数:4、6、2 的最大公约数是 2;
字母:相同字母
a
(最低次幂
a
1
)、
b
(最低次幂
b
1
);
公因式为
−2ab
(提负号后,括号内各项符号要改变)。
步骤 2:提公因式
−4a
3
b
2
÷(−2ab)=2a
2
b
,
6a
2
b÷(−2ab)=−3a
,
−2ab÷(−2ab)=1
;
分解结果:
−2ab(2a
2
b−3a+1)
。
类型 2:公因式为多项式(进阶题)
例 3:分解因式
3(x−y)−2(x−y)
2
步骤 1:找公因式
各项都含多项式因式
(x−y)
,最低次幂为
(x−y)
1
;
系数:3、-2 的最大公约数是 1;
公因式为
(x−y)
。
步骤 2:提公因式
3(x−y)÷(x−y)=3
,
−2(x−y)
2
÷(x−y)=−2(x−y)
;
分解结果:
(x−y)[3−2(x−y)]=(x−y)(3−2x+2y)
(括号内可整理,去括号后合并同类项)。
例 4:分解因式
a(x−3)+2b(3−x)
关键:注意
(3−x)=−(x−3)
,先统一公因式;
步骤 1:变形后找公因式
原式 =
a(x−3)−2b(x−3)
,公因式为
(x−3)
;
步骤 2:提公因式
分解结果:
(x−3)(a−2b)
。
四、易错点总结(避坑指南)
漏提系数的最大公约数:如将
4x
2
−6x
分解为
2x(x−3)
(错误,应为
2x(2x−3)
);
漏提相同字母的最低次幂:如将
x
3
y
2
−x
2
y
3
分解为
x
2
y(x−y
2
)
(错误,应为
x
2
y
2
(x−y)
);
提公因式后漏写 “1”:如将
2x+4
分解为
2(x)
(错误,应为
2(x+2)
);
符号错误:首项为负时未提负号,或提负号后括号内各项符号未改变;
公因式为多项式时未统一形式:如
(x−y)
和
(y−x)
需先转化为相同形式。
五、基础练习(巩固提升)
分解因式:
12x
3
y−18x
2
y
2
(答案:
6x
2
y(2x−3y)
)
分解因式:
−8a
2
b+12ab
2
−4ab
(答案:
−4ab(2a−3b+1)
)
分解因式:
5(x+2)−3(x+2)
2
(答案:
(x+2)(5−3x−6)=(x+2)(−3x−1)=−(x+2)(3x+1)
)
分解因式:
m(a−b)−n(b−a)
(答案:
(a−b)(m+n)
)
六、总结
提公因式法是因式分解的最基础、最常用方法,核心是 “找准公因式”,关键在于兼顾系数、字母、多项式因式的提取,同时注意符号和漏项问题。掌握此方法后,能为后续学习公式法、十字相乘法等复杂因式分解打下基础,解题时需遵循 “找→提→验” 的步骤,规范操作,避免易错点。](https://manimvideo.explanation.fun/video/cover/596037600963858433.png)
▶
八年级数学 / 因式分解 / 用提公因式法分解因式 一、核心概念(夯实基础) 1. 公因式的定义 一个多项式中各项都含有的公共因式,叫做这个多项式各项的公因式。 公因式的构成:① 系数部分:各项系数的最大公约数(若系数为负,取绝对值的最大公约数,最终公因式的符号由多项式首项符号决定,通常使首项为正);② 字母部分:各项中相同的字母,且取相同字母的最低次幂;③ 特殊情况:公因式可以是单项式,也可以是多项式(如 (a+b) 作为公共因式)。 示例:多项式 8a 3 b 2 −12ab 3 c 的公因式:系数部分:8 和 12 的最大公约数是 4;字母部分:相同字母为 a (最低次幂 a 1 )、 b (最低次幂 b 2 ),无公共字母 c ;因此公因式为 4ab 2 。 2. 提公因式法的定义 如果一个多项式的各项含有公因式,那么就可以把这个公因式提取出来,将多项式化成两个因式乘积的形式,这种因式分解的方法叫做提公因式法。 本质:逆用乘法分配律( ma+mb+mc=m(a+b+c) ,其中 m 为公因式)。 二、提公因式法的解题步骤(规范操作) 步骤 1:找公因式(关键步骤) 按 “系数→字母→多项式” 的顺序找,确保不遗漏:① 找系数的最大公约数(含符号处理);② 找相同字母的最低次幂;③ 若各项含有相同的多项式因式,将其视为一个整体作为公因式。 步骤 2:提公因式 用多项式的每一项除以公因式,得到另一个因式,公因式写在括号外,两个因式用乘法连接。 注意:提取公因式后,括号内的各项系数、字母次数要与原多项式对应,不能漏项。 步骤 3:验结果(避免出错) 用乘法分配律将分解后的式子展开,看是否与原多项式相等,若相等则分解正确。 三、典型例题(分层突破) 类型 1:公因式为单项式(基础题) 例 1:分解因式 6x 2 y−9xy 2 +3xy 步骤 1:找公因式 系数:6、-9、3 的最大公约数是 3; 字母:相同字母 x (最低次幂 x 1 )、 y (最低次幂 y 1 ); 公因式为 3xy 。 步骤 2:提公因式 每一项除以 3xy : 6x 2 y÷3xy=2x , −9xy 2 ÷3xy=−3y , 3xy÷3xy=1 ; 因此分解结果: 3xy(2x−3y+1) (注意:最后一项除以公因式得 1,不能漏写)。 步骤 3:验证 展开 3xy(2x−3y+1)=6x 2 y−9xy 2 +3xy ,与原多项式一致,正确。 例 2:分解因式 −4a 3 b 2 +6a 2 b−2ab 步骤 1:找公因式 首项为负,先提取 “-” 号,再找系数绝对值的最大公约数:4、6、2 的最大公约数是 2; 字母:相同字母 a (最低次幂 a 1 )、 b (最低次幂 b 1 ); 公因式为 −2ab (提负号后,括号内各项符号要改变)。 步骤 2:提公因式 −4a 3 b 2 ÷(−2ab)=2a 2 b , 6a 2 b÷(−2ab)=−3a , −2ab÷(−2ab)=1 ; 分解结果: −2ab(2a 2 b−3a+1) 。 类型 2:公因式为多项式(进阶题) 例 3:分解因式 3(x−y)−2(x−y) 2 步骤 1:找公因式 各项都含多项式因式 (x−y) ,最低次幂为 (x−y) 1 ; 系数:3、-2 的最大公约数是 1; 公因式为 (x−y) 。 步骤 2:提公因式 3(x−y)÷(x−y)=3 , −2(x−y) 2 ÷(x−y)=−2(x−y) ; 分解结果: (x−y)[3−2(x−y)]=(x−y)(3−2x+2y) (括号内可整理,去括号后合并同类项)。 例 4:分解因式 a(x−3)+2b(3−x) 关键:注意 (3−x)=−(x−3) ,先统一公因式; 步骤 1:变形后找公因式 原式 = a(x−3)−2b(x−3) ,公因式为 (x−3) ; 步骤 2:提公因式 分解结果: (x−3)(a−2b) 。 四、易错点总结(避坑指南) 漏提系数的最大公约数:如将 4x 2 −6x 分解为 2x(x−3) (错误,应为 2x(2x−3) ); 漏提相同字母的最低次幂:如将 x 3 y 2 −x 2 y 3 分解为 x 2 y(x−y 2 ) (错误,应为 x 2 y 2 (x−y) ); 提公因式后漏写 “1”:如将 2x+4 分解为 2(x) (错误,应为 2(x+2) ); 符号错误:首项为负时未提负号,或提负号后括号内各项符号未改变; 公因式为多项式时未统一形式:如 (x−y) 和 (y−x) 需先转化为相同形式。 五、基础练习(巩固提升) 分解因式: 12x 3 y−18x 2 y 2 (答案: 6x 2 y(2x−3y) ) 分解因式: −8a 2 b+12ab 2 −4ab (答案: −4ab(2a−3b+1) ) 分解因式: 5(x+2)−3(x+2) 2 (答案: (x+2)(5−3x−6)=(x+2)(−3x−1)=−(x+2)(3x+1) ) 分解因式: m(a−b)−n(b−a) (答案: (a−b)(m+n) ) 六、总结 提公因式法是因式分解的最基础、最常用方法,核心是 “找准公因式”,关键在于兼顾系数、字母、多项式因式的提取,同时注意符号和漏项问题。掌握此方法后,能为后续学习公式法、十字相乘法等复杂因式分解打下基础,解题时需遵循 “找→提→验” 的步骤,规范操作,避免易错点。
▶
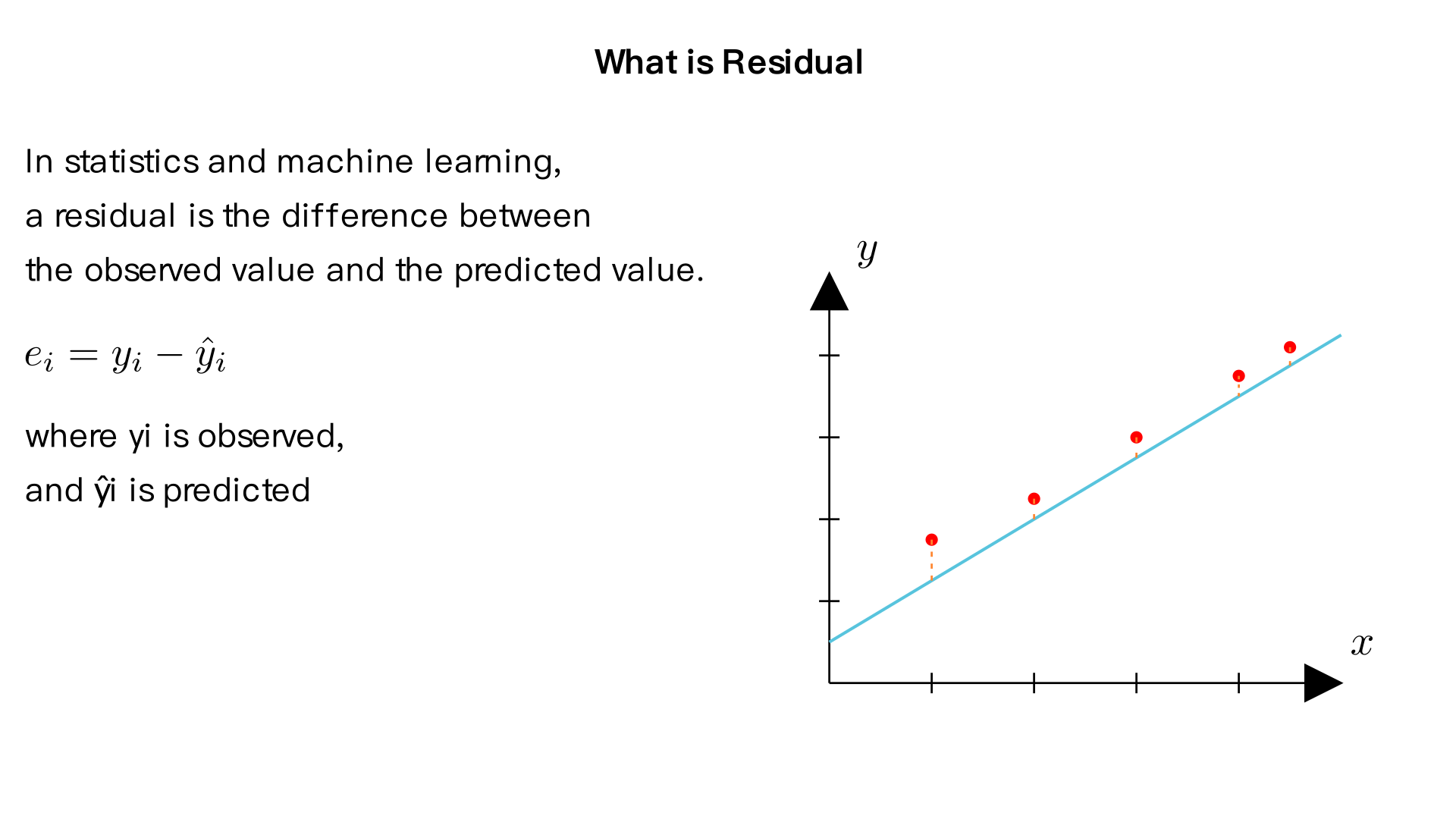
what is Residual

▶
什么是平均数
▶
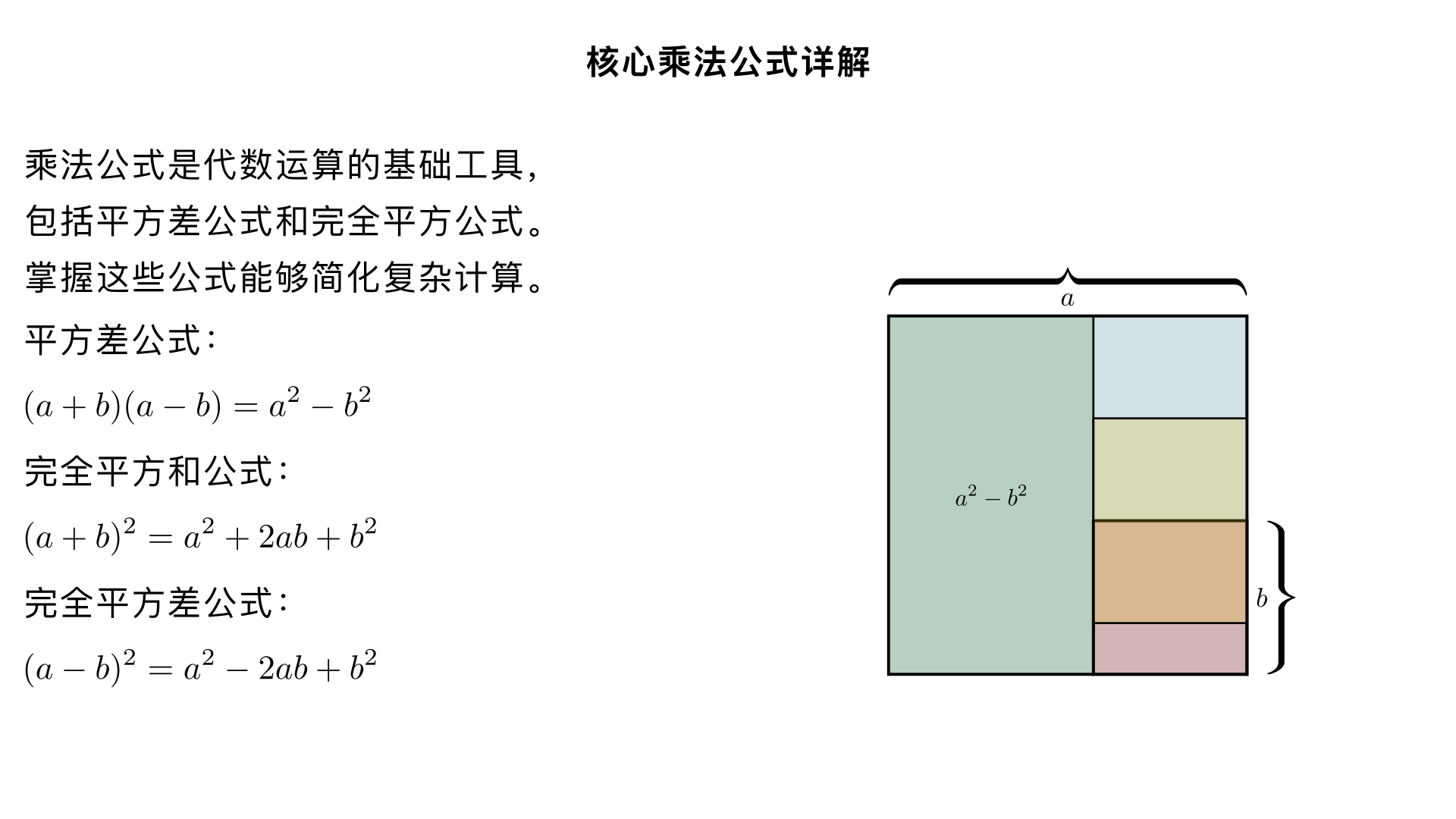
二、核心乘法公式详解 1. 平方差公式 标准形式: (a+b)(a−b)=a 2 −b 2 语言描述:两数和与这两数差的积,等于这两数的平方差 推导过程(多项式乘法展开): (a+b)(a−b) =a⋅a+a⋅(−b)+b⋅a+b⋅(−b) =a 2 −ab+ab−b 2 =a 2 −b 2 结构特点: 左边:两个二项式相乘,其中一项完全相同( a ),另一项互为相反数( b 与 −b ) 右边:相同项的平方减去相反项的平方(同方减反方) 几何意义:边长为 a 的正方形中挖去边长为 b 的小正方形,剩余部分面积为 a 2 −b 2 ,可拼成一个长 (a+b) 、宽 (a−b) 的矩形 2. 完全平方公式(和与差) 完全平方和公式: 标准形式: (a+b) 2 =a 2 +2ab+b 2 语言描述:两数和的平方,等于它们的平方和加上它们积的 2 倍 完全平方差公式: 标准形式: (a−b) 2 =a 2 −2ab+b 2 语言描述:两数差的平方,等于它们的平方和减去它们积的 2 倍 推导过程(以和为例): (a+b) 2 =(a+b)(a+b) =a⋅a+a⋅b+b⋅a+b⋅b =a 2 +2ab+b 2 结构特点(口诀:首平方,尾平方,积的 2 倍在中央): 左边:二项式的平方(两个相同二项式相乘) 右边:三项式,包含首项平方( a 2 )、尾项平方( b 2 )、中间交叉项的 2 倍( ±2ab ),符号与左边二项式中间符号相同 几何意义(以和为例):边长为 a+b 的正方形,可分为边长为 a 的正方形、边长为 b 的正方形,以及两个长 a 宽 b 的矩形,面积和为 a 2 +2ab+b 2 三、公式的灵活应用 1. 基本应用:直接套用公式 平方差公式示例: (x+3)(x−3)=x 2 −3 2 =x 2 −9 (2a+5b)(2a−5b)=(2a) 2 −(5b) 2 =4a 2 −25b 2 完全平方公式示例: (m+4) 2 =m 2 +2⋅m⋅4+4 2 =m 2 +8m+16 (3x−2y) 2 =(3x) 2 −2⋅3x⋅2y+(2y) 2 =9x 2 −12xy+4y 2

▶