T
Teach Me AnythingTMA
Video History
Page 6 / 44
▶
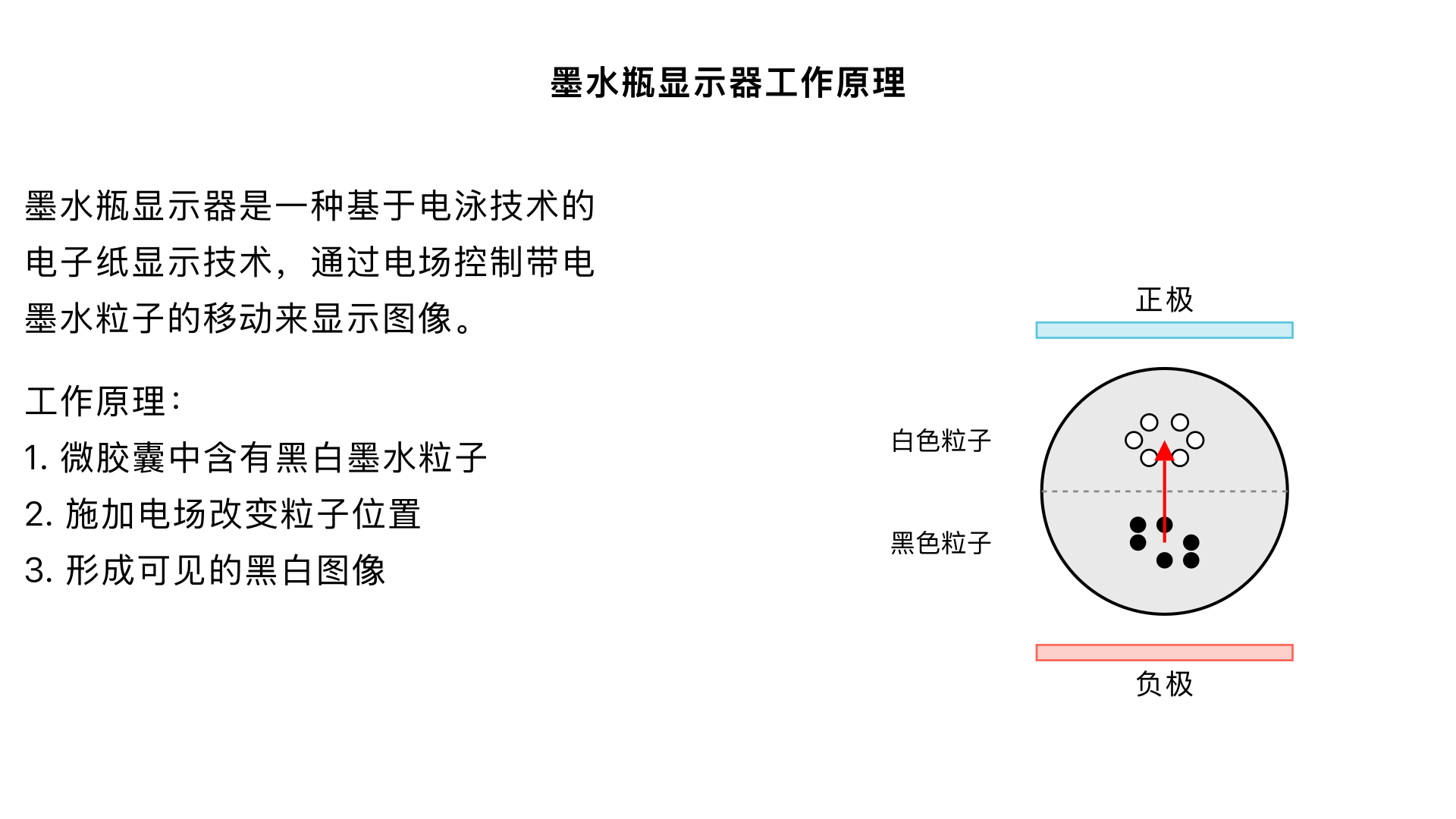
困与井——困境中的坚守与通达 一、困卦(泽水困):困境中的德性考验 1. 卦序与卦象 《序卦传》:“升而不已必困,故受之以困。” 上升不止必遇困阻。 卦象:上兑泽,下坎水(䷮),泽中无水,象征困穷。 卦德:坎险兑悦,虽处险境而能乐观。 2. 《彖传》精解 text 困,刚揜也。 险以说,困而不失其所亨,其唯君子乎? 贞大人吉,以刚中也。 有言不信,尚口乃穷也。 “刚揜也”:阳刚被掩蔽(九二被初六、六三所掩,九五被上六所掩)。 “险以说”:下坎险,上兑悦。 “困而不失其所亨”:困境中不丧失亨通之道。 “有言不信”:此时说话无人信,崇尚口舌只会穷困。 3. 《大象传》:“泽无水,困。君子以致命遂志。” 泽中无水,君子因此不惜生命以实现志向(杀身成仁)。 4. 爻辞精析 初六:臀困于株木,入于幽谷,三岁不觌。 臀部受困于树根,进入幽谷,三年不见天日(困于底层)。 九二:困于酒食,朱绂方来,利用享祀,征凶,无咎。 困于酒食(俸禄微薄),荣禄(朱绂)将来,宜祭祀,出征凶但终无咎。 六三:困于石,据于蒺藜,入于其宫,不见其妻,凶。 困在石中,凭据蒺藜上,回到家中不见妻子,凶(进退失据)。 九四:来徐徐,困于金车,吝,有终。 缓缓而来,被金车所困(受权贵所阻),有憾惜,但有好终。 九五:劓刖,困于赤绂,乃徐有说,利用祭祀。 像受劓刖之刑,困于尊位(赤绂),但渐渐有喜悦,利于祭祀。 上六:困于葛藟,于臲卼,曰动悔。有悔,征吉。 困于葛藤缠绕,动摇不安,动辄有悔;但能悔悟,出征则吉。 二、井卦(水风井):养人不变的井德 1. 卦序与卦象 《序卦传》:“困乎上者必反下,故受之以井。” 困穷于上必然返归于下,井是居下养上的象征。 卦象:上坎水,下巽木(䷯),木上有水,以木桶汲水,象征水井。 卦德:巽入坎水,深入取水,养人不穷。 2. 《彖传》精解 text 巽乎水而上水,井。 井养而不穷也。 改邑不改井,乃以刚中也。 汔至亦未繘井,未有功也。 羸其瓶,是以凶也。 “巽乎水而上水”:下巽入,上坎水,入水而提水。 “井养而不穷”:井水养人,永不穷竭。 “改邑不改井”:村落可改,水井不移,因九二、九五刚中守常。 “羸其瓶,凶”:打破汲瓶,凶。 3. 《大象传》:“木上有水,井。君子以劳民劝相。” 木上有水,君子因此慰劳百姓,劝勉互助。 4. 爻辞精析 初六:井泥不食,旧井无禽。 井底有泥不可食,旧井无禽鸟光顾(井已废)。 九二:井谷射鲋,瓮敝漏。 井水漏失如射小鱼,瓮破漏水(井失其用)。 九三:井渫不食,为我心恻。可用汲,王明并受其福。 井已淘净却无人食用,令人心恻;可汲用,君王明察则君臣同福。 六四:井甃,无咎。 井壁修砌,无咎(井在修复)。 九五:井冽寒泉,食。 井水清冽如寒泉,可食(井德完美)。 上六:井收勿幕,有孚元吉。 井功已成,不盖井口,有诚信大吉(开放共享)。 三、困井二卦的对比 困与通的转化:困卦是困境,井卦是通养;困极则返下求通,如井养不穷。 德性考验:困卦考验“致命遂志”,井卦考验“劳民劝相”。 井卦的永恒价值:“改邑不改井”象征不变的美德,“井养不穷”象征持续的贡献。 金景芳指出:井卦强调“养人”的功德,个人应修德如修井,终能惠及他人。
▶
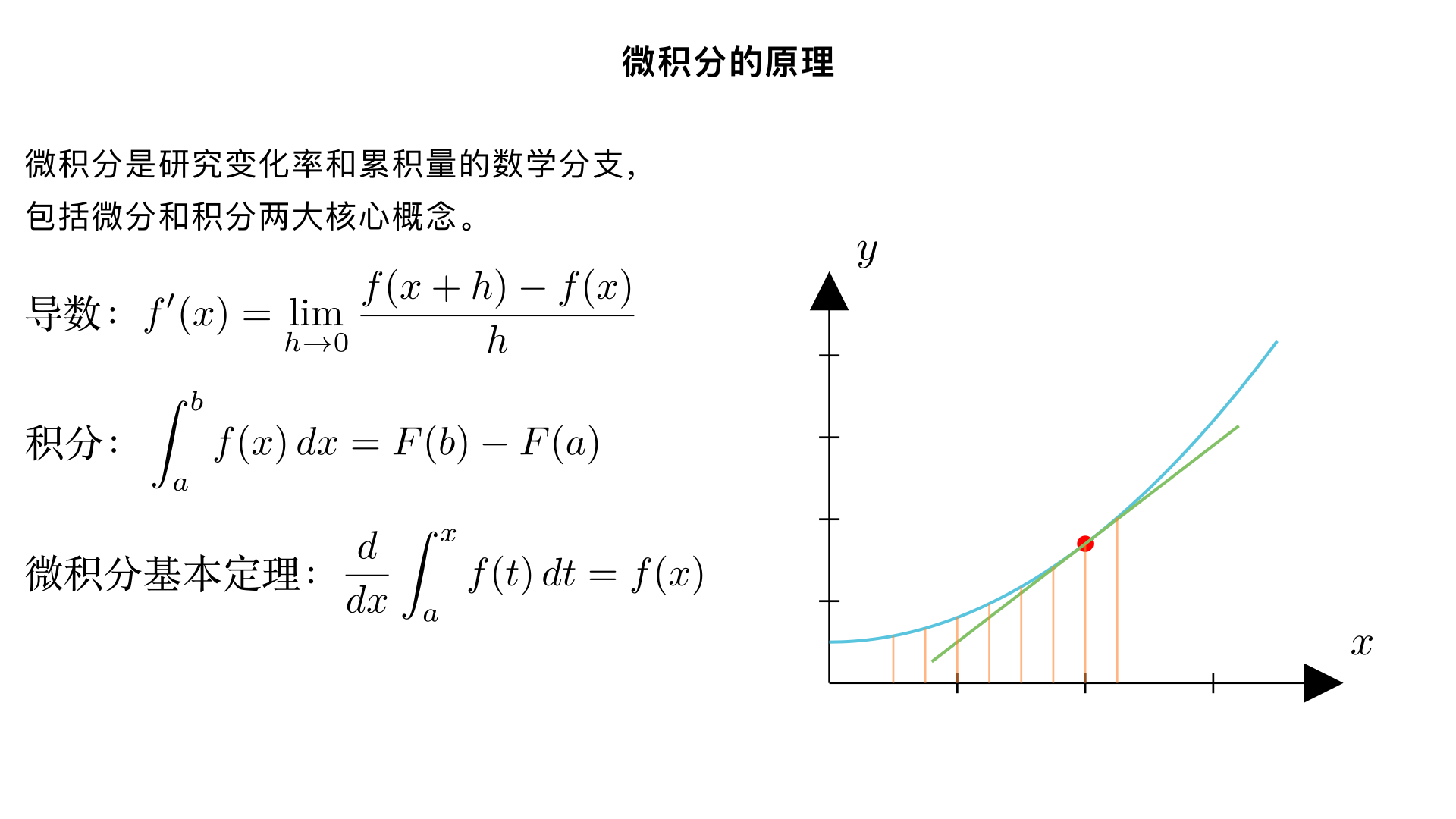
墨水瓶显示器工作原理
▶
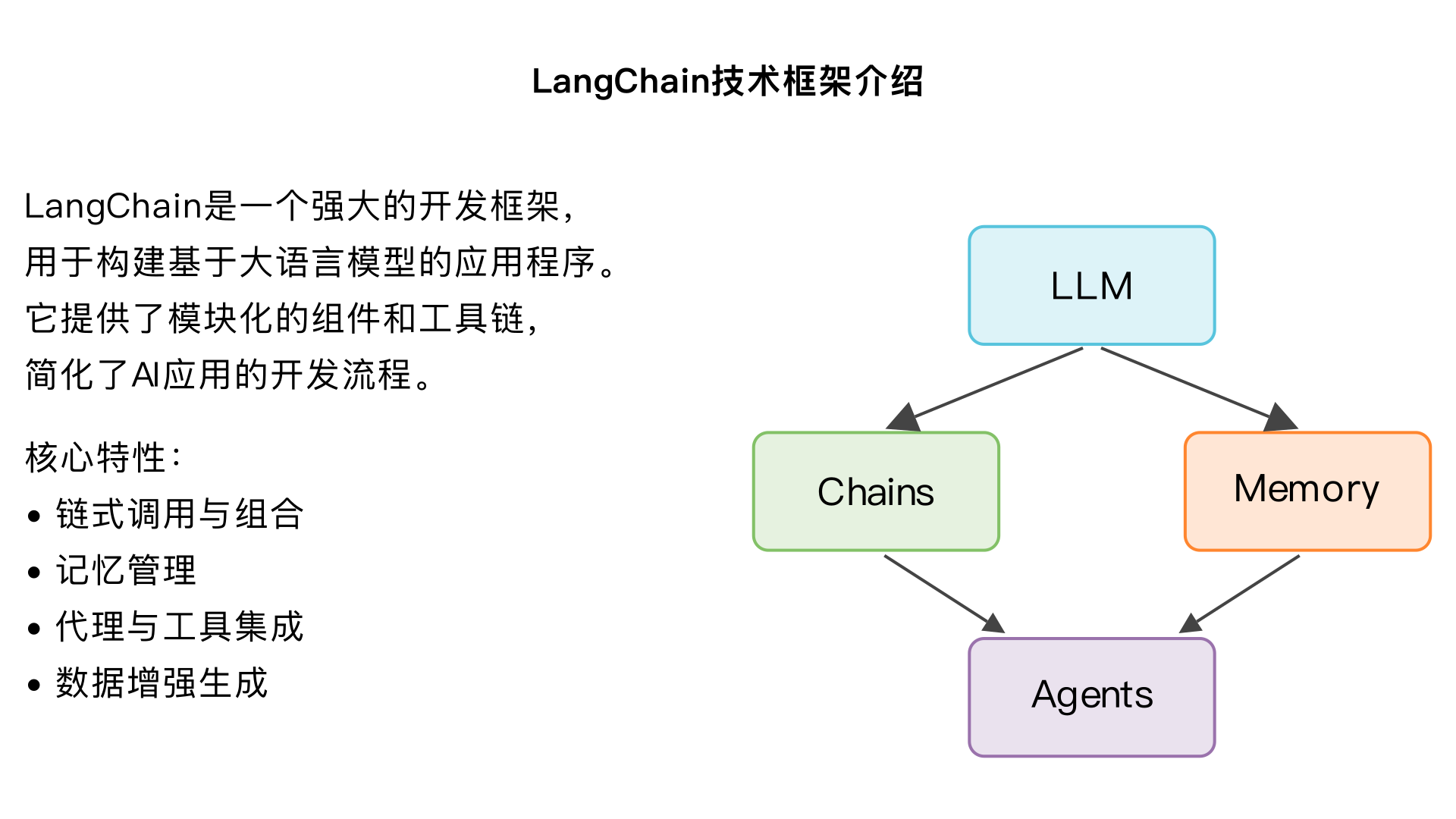
微积分的原理
▶
请给我介绍一下langchain这个技术框架
▶
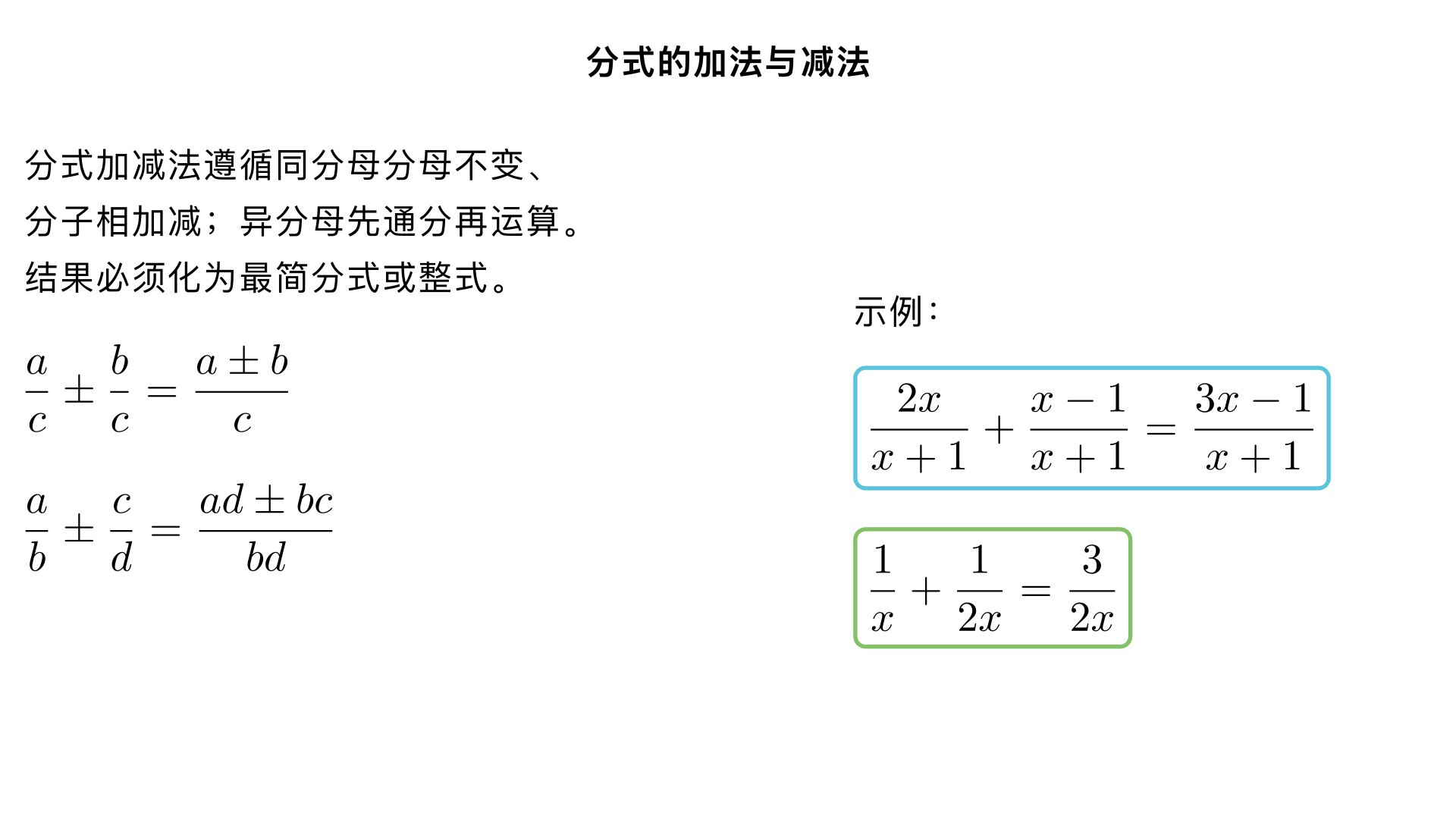
八年级数学 / 分式 / 分式的加法与减法 核心要点速览:分式加减法遵循 “同分母分母不变、分子相加减;异分母先通分再运算”,结果必须化为最简分式或整式,关键在于符号处理与通分两大环节。 一、同分母分式的加减法 1. 法则(类比同分母分数加减法) 同分母分式相加减,分母不变,把分子相加减。字母表示: c a ± c b = c a±b ( c =0 ) 2. 运算步骤 保持分母不变,将各分式分子用括号括起来,再进行加减 去括号,合并同类项(特别注意减号后的符号变化) 约分,化为最简分式或整式 3. 例题与解析 例 1:计算 x+1 2x + x+1 x−1 解:原式 = x+1 2x+(x−1) (分子相加,分母不变)= x+1 2x+x−1 (去括号)= x+1 3x−1 (合并同类项,已是最简) 例 2:计算 a−2 3a − a−2 a+4 解:原式 = a−2 3a−(a+4) (分子相减,注意括号)= a−2 3a−a−4 (去括号,减号后变号)= a−2 2a−4 (合并同类项)= a−2 2(a−2) (因式分解)= 2 (约分,结果为整式, a =2 ) 4. 注意事项 分子是多项式时,必须加括号,防止符号错误 结果要约分,保证是最简分式或整式 分母不能为零,注意隐含条件(如例 2 中 a =2 ) 二、异分母分式的加减法 1. 法则(类比异分母分数加减法) 异分母分式相加减,先通分,化为同分母分式,再按同分母分式加减法法则计算。字母表示: b a ± d c = bd ad±bc ( b =0 , d =0 ) 2. 关键:通分与最简公分母 通分:将几个异分母分式化为与原分式相等的同分母分式的过程,依据是分式基本性质。最简公分母:取各分母系数的最小公倍数与各字母(或因式)的最高次幂的积。 3. 确定最简公分母的方法 分母类型 确定方法 示例 单项式 1. 系数:最小公倍数 2. 字母:各字母最高次幂 分母 2x 2 y 与 3xy 3 ,最简公分母 6x 2 y 3 多项式 1. 先因式分解 2. 取各因式最高次幂 3. 系数最小公倍数 分母 x 2 −4 ( =(x+2)(x−2) )与 x−2 ,最简公分母 (x+2)(x−2) 4. 运算步骤 对各分母因式分解,确定最简公分母 用分式基本性质,将每个分式化为以最简公分母为分母的等价分式 按同分母分式加减法法则计算 结果约分,化为最简形式 5. 例题与解析 例 3:计算 x 1 + 2x 1 解: 最简公分母: 2x 通分: x 1 = 2x 2 , 2x 1 不变 计算: 2x 2 + 2x 1 = 2x 3 (已是最简) 例 4:计算 x−1 3 − x+1 2 解: 最简公分母: (x−1)(x+1)=x 2 −1 通分: x−1 3 = (x−1)(x+1) 3(x+1) , x+1 2 = (x−1)(x+1) 2(x−1) 计算: (x−1)(x+1) 3(x+1)−2(x−1) 分子化简: 3x+3−2x+2=x+5 结果: x 2 −1 x+5 ( x =±1 ) 三、分式加减法的特殊情况与技巧 1. 符号处理技巧 分式前面有负号: b a − d c = b a +(− d c ) ,分子整体变号 分母为相反数: a−b 1 =− b−a 1 ,可先统一符号再计算 例 5:计算 x−y 1 + y−x 1 解:原式 = x−y 1 − x−y 1 = x−y 1−1 =0 ( x =y ) 2. 含整式的分式加减法 整式可视为分母为 1 的分式,再通分计算。例 6:计算 x+ x−1 1 解:原式 = x−1 x(x−1) + x−1 1 = x−1 x 2 −x+1 ( x =1 ) 3. 混合运算(先乘除后加减,有括号先算括号内) 例 7:计算 x+1 x − x−1 1 ⋅ x x 2 −1 解: 先算乘法: x−1 1 ⋅ x (x+1)(x−1) = x x+1 再算减法: x+1 x − x x+1 = x(x+1) x 2 −(x+1) 2 = x(x+1) x 2 −x 2 −2x−1 =− x(x+1) 2x+1 ( x =0,±1 ) 四、常见错误与避错指南 常见错误 错误原因 正确做法 同分母分式加减时分母也参与运算 混淆分数与分式运算法则 牢记 “分母不变,只把分子相加减” 分子是多项式时不加括号,导致符号错误 忽略减号对分子整体的影响 分子是多项式必须加括号,去括号时注意变号 通分时最简公分母确定错误 系数未取最小公倍数或字母未取最高次幂 严格按 “系数最小公倍数 × 字母最高次幂” 确定 结果未约分 忘记分式运算的最终要求 养成 “先因式分解,再约分” 的习惯 忽略分母不为零的条件 缺乏定义域意识 每步运算都要检查分母是否为零,结果注明限制条件 五、巩固练习(附答案) 基础题 a 3 + a 2 = a 5 ( a =0 ) x−2 x+1 − x−2 x−3 = x−2 4 ( x =2 ) 2x 1 + 3x 1 = 6x 5 ( x =0 ) 提高题 x+3 2 + x−3 1 = (x+3)(x−3) 3x−3 ( x =±3 ) x 2 −4 x − 4−x 2 2 = (x+2)(x−2) x+2 = x−2 1 ( x =±2 ) 六、思维导图(知识结构) plaintext 分式加减法 ├─ 同分母分式加减法:分母不变,分子相加减(结果必约分) ├─ 异分母分式加减法:先通分→再按同分母法则计算 │ └─ 通分关键:确定最简公分母(系数最小公倍数×字母最高次幂) ├─ 特殊情况: │ ├─ 符号处理(分母互为相反数时先统一符号) │ ├─ 含整式的运算(整式视为分母为1的分式) │ └─ 混合运算(先乘除后加减,有括号先算括号内) └─ 核心要求:结果必须化为最简分式或整式,注意分母不为零 总结:分式加减法的本质是 “转化思想”—— 异分母转化为同分母,复杂转化为简单。掌握法则是基础,符号处理和通分技巧是关键,结果约分是保障,多加练习就能熟练掌握这一重要的代数运算技能。
▶
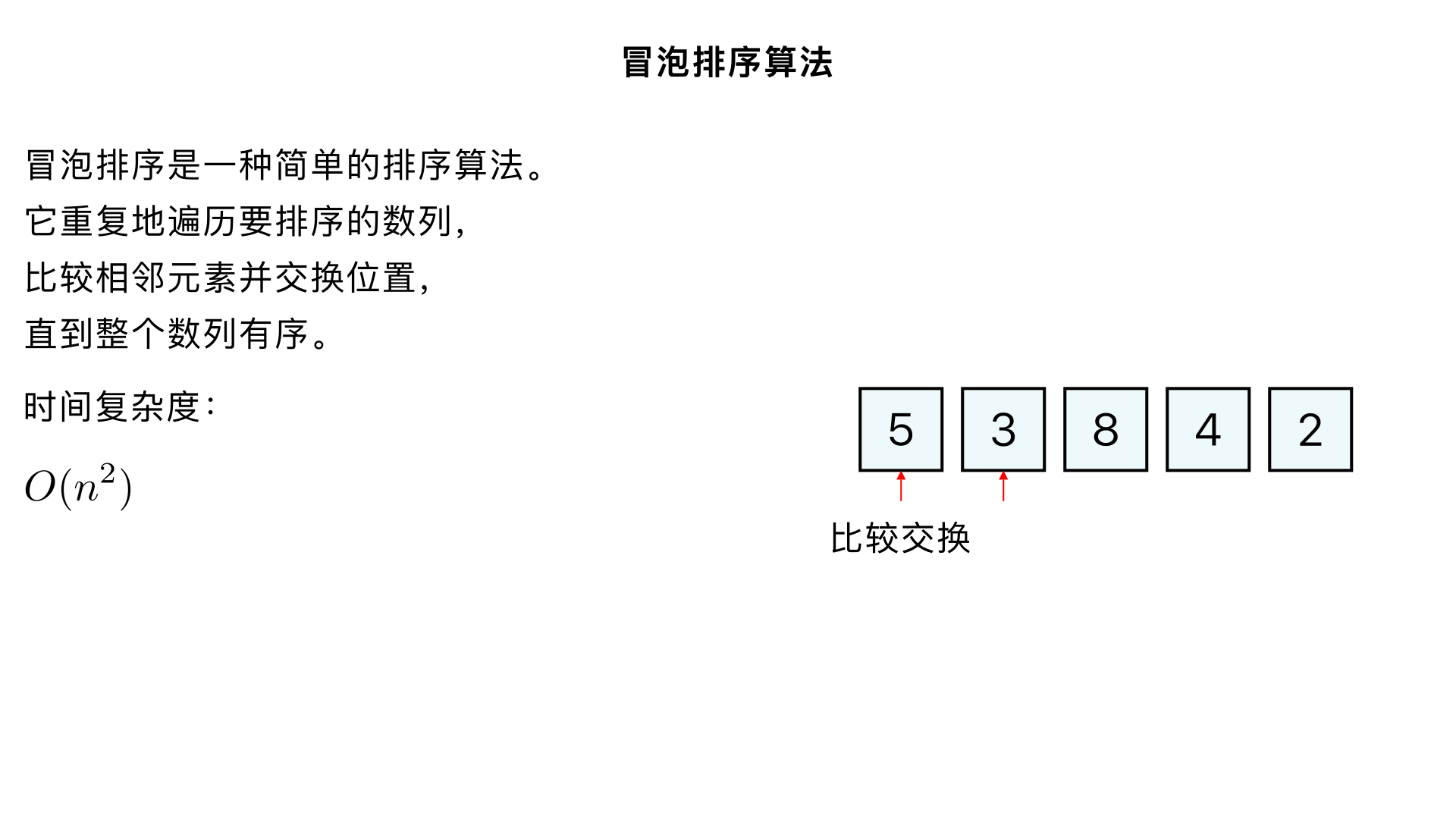
帮我解释下冒泡排序的过程
▶
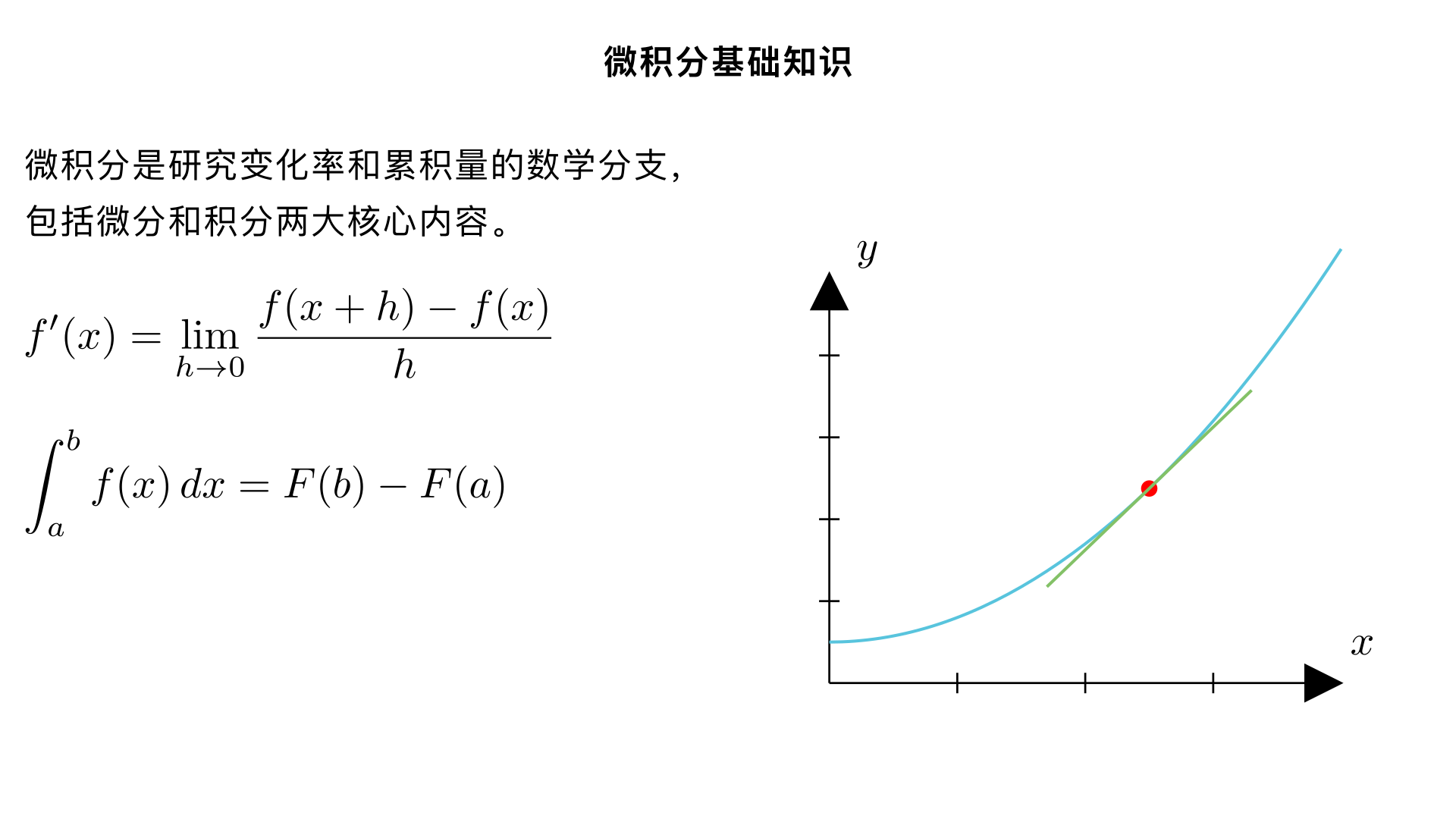
你是一名专业的高中数学老师,我想了解下微积分的知识点,请详细分步骤从浅到深介绍下

▶
八年级数学 / 分式 / 分式的乘法与除法 一、核心法则(必背) 1. 分式乘法法则 两个分式相乘,分子相乘的积作为积的分子,分母相乘的积作为积的分母。字母表示: b a × d c = b×d a×c = bd ac (其中 a,b,c,d 是整式,且 bd =0 )。 2. 分式除法法则 分式除以分式,等于被除式乘以除式的倒数(即将除式的分子、分母颠倒位置后再相乘)。字母表示: b a ÷ d c = b a × c d = bc ad (其中 a,b,c,d 是整式,且 bcd =0 )。 二、运算步骤(四步法) 1. 准备阶段 符号判断:数负号个数,偶数个为正,奇数个为负,先确定结果符号。 整式处理:整式看作分母为 1 的分式,如 5= 1 5 。 多项式因式分解:分子或分母为多项式时,先分解因式(提公因式、平方差、完全平方等)。 2. 转化阶段(除法专用) 将除号变为乘号,同时把除式的分子分母颠倒位置,转化为乘法运算。 3. 计算阶段 分子相乘、分母相乘,写成一个分式形式。 4. 化简阶段(关键步骤) 约分:分子分母同时除以它们的公因式,直至化为最简分式(分子分母没有公因式)或整式。 技巧:先约分再相乘,可简化计算量。 三、典型例题解析 例 1:单项式分式乘法 计算: 3y 2x × 4x 2 9y 2 步骤: 符号:正(无负号) 直接相乘: 3y×4x 2 2x×9y 2 约分(先约更简便): 3y×4x 2 2x×9y 2 = 3y ×2× 2x ×x 2x × 3y ×3y = 2x 3y 结果: 2x 3y 例 2:多项式分式乘法 计算: x 2 +2x x 2 −4 × x−2 x 步骤: 因式分解: x 2 −4=(x+2)(x−2) , x 2 +2x=x(x+2) 代入原式: x(x+2) (x+2)(x−2) × x−2 x 约分(约去公因式 x 、 x+2 、 x−2 ): x (x+2) (x+2) (x−2) × x−2 x =1 结果: 1 例 3:分式除法 计算: a 2 +6a+9 a 2 −9 ÷ a+3 a−3 步骤: 因式分解: a 2 −9=(a+3)(a−3) , a 2 +6a+9=(a+3) 2 转化为乘法: (a+3) 2 (a+3)(a−3) × a−3 a+3 约分(约去公因式 a+3 、 a−3 ): (a+3) 2 (a+3) (a−3) × a−3 a+3 =1 结果: 1 例 4:混合运算(含整式) 计算: 6x 2 y÷ 2z 3xy 2 步骤: 整式变分式: 6x 2 y= 1 6x 2 y 转化为乘法: 1 6x 2 y × 3xy 2 2z 约分计算: 3xy 2 6x 2 y×2z = 3 × x × y ×y 3 ×2× x ×x× y ×2z = y 4xz 结果: y 4xz 四、注意事项(易错点警示) 分母不为零:运算中始终保证所有分母及除式不为零,即 b =0 , d =0 (乘法); b =0 , c =0 , d =0 (除法)。 先约后乘:切勿先盲目相乘再约分,易导致计算复杂且出错。 符号问题:单独的负号可看作分母为 1 的分式,如 −a= 1 −a ;注意分子或分母是多项式时,负号要分配到每一项。 结果要求:最终结果必须是最简分式或整式,不能保留能约分的形式。 因式分解要彻底:分解不彻底会导致无法正确约分,如 x 2 −4 必须分解为 (x+2)(x−2) ,不能停留在 x 2 −4 阶段。 五、知识体系与衔接 前导知识:分数乘除法、因式分解、分式基本性质。 后续知识:分式的乘方、分式的混合运算、分式方程。 核心思想:类比分数乘除法法则,利用 “数式通性” 将分数运算推广到分式运算,体现转化与化归的数学思想。
▶
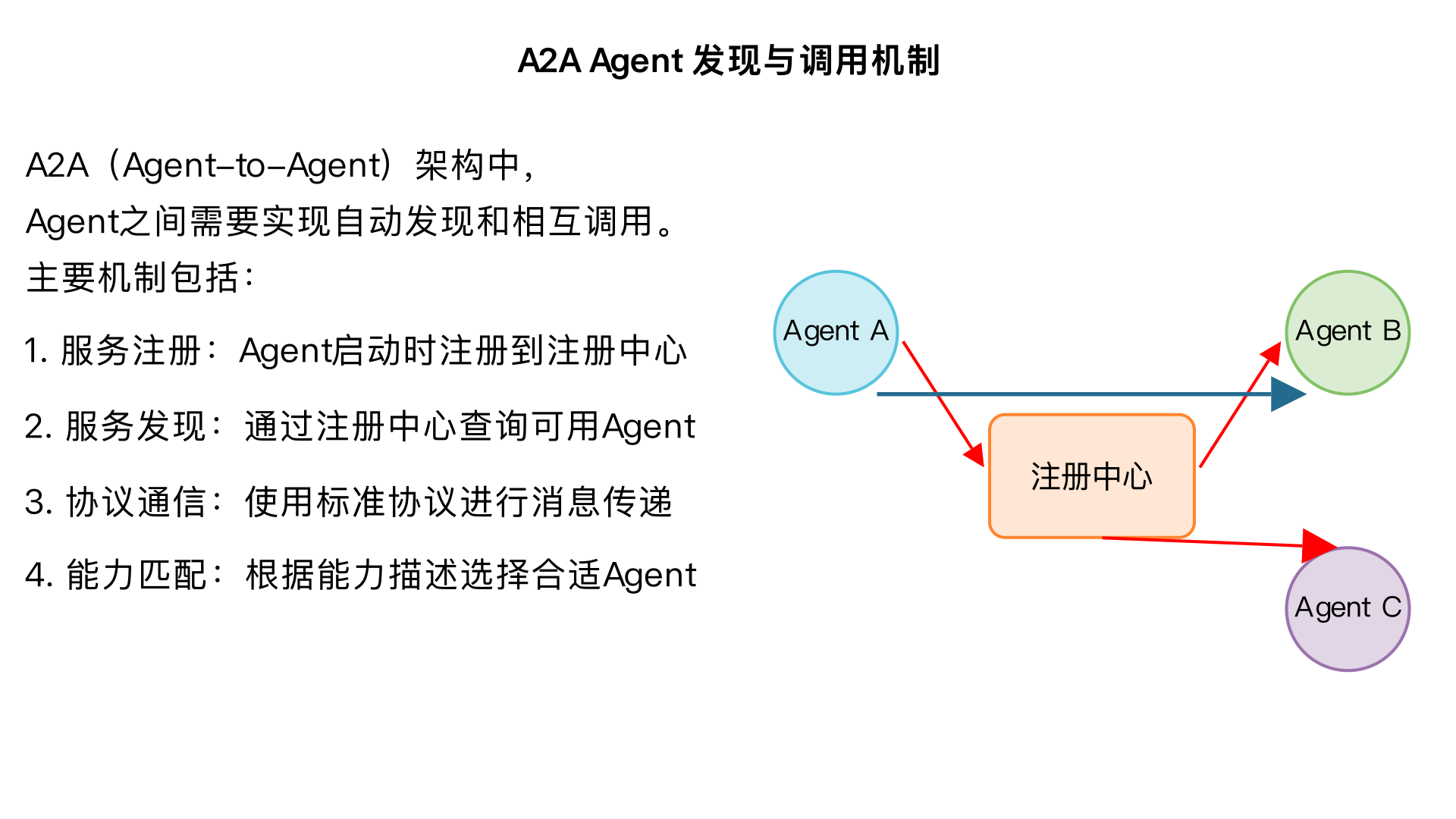
a2a agent 之间是如何实现 agent 发现和调用的

▶
The image is not a geometric figure. **Chart/Diagram Description:** * **Type:** Botanical illustration/drawing. * **Main Elements:** The image displays a detailed, realistic illustration of a single tree, characteristic of a Dragon's Blood Tree (genus Dracaena). * **Trunk:** The tree has a thick, robust, and gnarled main trunk with deep fissures and textures, colored in various shades of dark brown. Near the center, there is a prominent split or cavity in the trunk revealing a reddish substance, consistent with the "dragon's blood" resin. The base of the trunk is wide and appears firmly rooted. * **Branches:** Numerous thick, contorted branches extend upwards and outwards from the main trunk, creating a dense, spreading structure. These branches are also dark brown and highly textured. * **Foliage/Crown:** The tree features a very dense, umbrella-shaped crown composed of numerous rosettes of spiky, sword-like leaves. The leaves are predominantly dark green with hints of olive green and some reddish-brown or bronze tones, especially visible on older leaves or leaf bases. * **Overall Form:** The tree exhibits the classic mature form of a Dragon's Blood Tree, with a sturdy trunk branching into a broad, flat, and densely foliated canopy. * **Background:** The background is a plain, light off-white or cream color, providing high contrast for the tree. * **Labels and Annotations:** No text labels, annotations, or coordinate axes are present in the image. * **Artistic Style:** The illustration is highly detailed, appearing to be a traditional painting or drawing, possibly a watercolor or gouache, given the texture and color blending. 解释一下这个图
▶
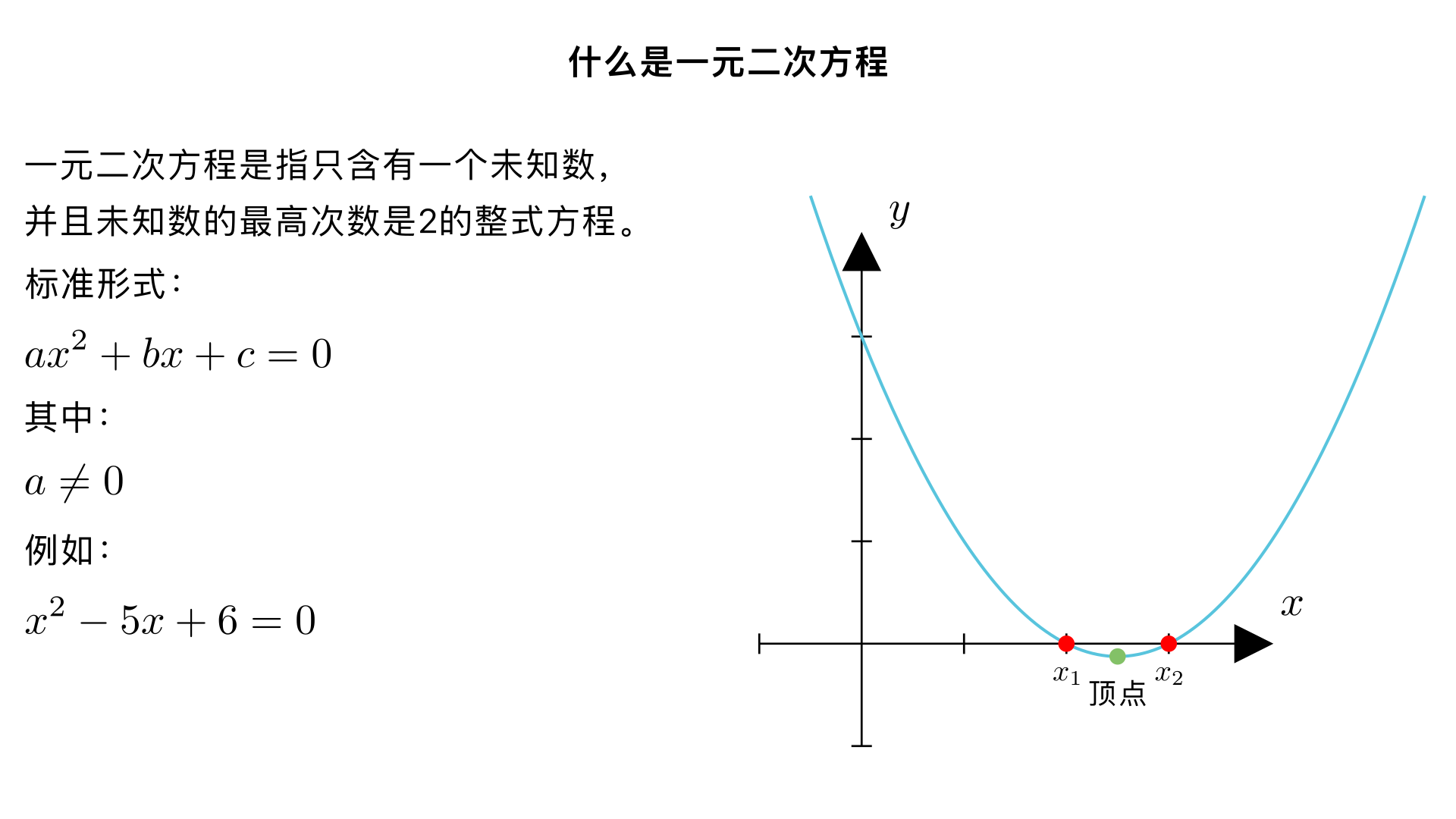
解释一下什么是一元二次方程
![八年级数学 / 分式 / 分式及其基本性质
一、分式的定义(核心概念)
1. 定义
一般地,如果
A
、
B
表示两个整式,并且
B
中含有字母,那么式子
B
A
叫做分式(fraction)。
其中
A
叫做分式的分子,
B
叫做分式的分母。
注意:分式的分母必须含有字母,且分母不能为 0(分母为 0 时分式无意义)。
2. 分式与整式的区别
类别 定义(核心特征) 示例
整式 分母不含字母的代数式(单项式或多项式)
3x
、
5
2
a
2
b
、
x+y−1
分式 分母含字母的代数式
x
1
、
x−3
x+2
、
a
2
+b
2
ab
3. 典型例题(判断分式)
例:下列式子中,哪些是分式?哪些是整式?
x
2
、
3
x
、
x+y
1
、
x−1
x
2
−1
、
0
、
5
ab
解:
分式:
x
2
(分母含
x
)、
x+y
1
(分母含
x,y
)、
x−1
x
2
−1
(分母含
x
);
整式:
3
x
(分母为常数 3)、
0
(单独常数)、
5
ab
(分母为常数 5)。
二、分式有意义、无意义及值为 0 的条件(高频考点)
1. 分式有意义的条件
分母不为 0,即
B
=0
(
A
可以为任意整式)。例:分式
2x−3
x+1
有意义的条件是
2x−3
=0
,解得
x
=
2
3
。
2. 分式无意义的条件
分母为 0,即
B=0
(与有意义的条件相反)。例:分式
x
2
−4
5
无意义的条件是
x
2
−4=0
,解得
x=2
或
x=−2
。
3. 分式值为 0 的条件(双重要求)
分子为 0:
A=0
;
分母不为 0:
B
=0
(缺一不可,否则分式无意义或值不为 0)。
例:分式
x+1
x
2
−1
值为 0 的条件是:
{
x
2
−1=0
x+1
=0
,解得
x=1
(注意:
x=−1
时分母为 0,需排除)。
三、分式的基本性质(核心性质,类比分数)
1. 基本性质
分式的分子与分母同乘(或除以)一个不等于 0 的整式,分式的值不变。用式子表示为:
B
A
=
B⋅C
A⋅C
,
B
A
=
B÷C
A÷C
(其中
C
是不等于 0 的整式)。
2. 关键注意事项
前提:
C
=0
(若
C=0
,则分母乘 0 后为 0,分式无意义);
类比:与分数的基本性质一致(分数是分式的特殊形式,分母为常数),例如
3
2
=
3×4
2×4
=
12
8
,分式
y
x
=
y⋅2
x⋅2
=
2y
2x
(
2
=0
);
范围:分子、分母需同时乘(或除以)同一个整式,不能只乘分子或只乘分母。
3. 性质的应用场景
化简分式(约分);
通分(分式加减法的基础);
分式变形(如将分子分母的符号转化)。
四、分式的符号法则(由基本性质推导)
1. 符号法则
分式的分子、分母与分式本身的符号,改变其中任意两个,分式的值不变。用式子表示为:
B
A
=
−B
−A
=−
B
−A
=−
−B
A
2. 应用技巧
若分子或分母是多项式,改变符号时需变多项式中每一项的符号,例如
2−x
x−3
=
−(x−2)
−(3−x)
=
x−2
3−x
;
通常将分式的分母化为正数,方便后续计算,例如
−x+5
2
=
5−x
2
。
五、分式的约分(基本性质的应用 1)
1. 定义
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分。
2. 约分的步骤
分解因式:将分子、分母分别分解因式(提公因式、平方差、完全平方等);
找出公因式:分子分母中相同因式的最低次幂的积;
约去公因式:分子分母同时除以公因式,得到最简分式。
3. 最简分式(约分的目标)
分子与分母没有公因式的分式叫做最简分式(也叫既约分式)。例:约分
4(x−1)
2
2x(x−1)
解:
分解因式:分子
2x(x−1)
,分母
4(x−1)
2
=2
2
(x−1)
2
;
公因式:
2(x−1)
;
约分:
4(x−1)
2
÷[2(x−1)]
2x(x−1)÷[2(x−1)]
=
2(x−1)
x
(最简分式)。
六、分式的通分(基本性质的应用 2)
1. 定义
根据分式的基本性质,把几个异分母的分式分别化为与原来的分式相等的同分母的分式,叫做分式的通分。
2. 通分的步骤
找最简公分母:取各分母所有因式的最高次幂的积(类比分数的最小公倍数);
分子分母同乘:每个分式的分子分母同时乘一个整式,使分母变为最简公分母。
3. 最简公分母的确定方法
系数:取各分母系数的最小公倍数;
字母(或因式):取各分母中所有字母(或因式)的最高次幂;
例:通分
2x
2
y
1
和
4xy
2
3
解:
最简公分母:系数最小公倍数
4
,字母
x
2
y
2
,即
4x
2
y
2
;
通分:
2x
2
y
1
=
2x
2
y×2y
1×2y
=
4x
2
y
2
2y
,
4xy
2
3
=
4xy
2
×x
3×x
=
4x
2
y
2
3x
。
七、易错点总结(避坑指南)
忽略分母不为 0 的条件:判断分式有意义、值为 0 时,必须先保证分母≠0;
约分 / 通分时出错:
约分只约公因式,不能约去 “单独的项”(例如
x+2
x+1
不能约去
x
);
通分找错最简公分母(尤其是分母含多项式时,需先分解因式);
符号变形错误:改变分子或分母符号时,忘记变多项式的每一项符号;
混淆 “分式基本性质” 与 “等式性质”:分式变形是 “分子分母同乘 / 除同一个不为 0 的整式”,而非 “两边同乘 / 除”(等式变形是两边操作)。](https://manimvideo.explanation.fun/video/cover/596750323375452160.png)
▶